
その他のサイクル記事
このIVの部分では、AES-128暗号の説明を完了します。これまでの作業に慣れていない読者のために、この資料は教育目的で提示されており、多くの機能(詳細、数値例、数学的基礎など)を課していることを説明します。 、および暗号化および復号化アルゴリズムの開発のために提示された資料の使用(鍵がない場合)。多くの有名なオンライン(およびオフライン)出版物の著者は、そのような目標を設定していなかったため、これらの出版物は私たちの目的にはほとんど役に立ちません。
暗号化の逆のプロセスは、メッセージの復号化と呼ばれます。(キーを使用して)暗号文(ST)を復号化するには、逆置換テーブルとラウンドキーを作成します。これらは、暗号化スキームとは逆の順序で使用されますが、暗号化プロセスと同様です。
AESメッセージの復号化
メッセージを復号化する操作のリストは、暗号化の場合と同じです。操作の詳細については、こちらをご覧ください。これは、かなり一般的な暗号の原則です。暗号化と復号化のための単一のハードウェア実装であり、両方のプロセスに対して同じ関数のセットによって提供されます。ソーステキストとキー送信のシーケンスのみが変更されます。
メッセージを復号化するプロセスは、暗号化に使用される一連の逆(逆)変換として、暗号化中のシーケンスとは逆の順序で実装されます。ラウンドキーが適切な順序で使用されていることも明らかです。最初に最後に受信したキー、次に最後から2番目のキーというように、最初のラウンドキーまで続きます。
すべての変換名は同じままですが、先頭にInvが付きます。以前と同じシーケンスでそれらを検討します。AES暗号では、リバースとフォワードの2つの復号化オプションを使用できます。これらについては、以下で詳しく説明します。
逆復号オプション
メッセージの逆復号化は、暗号化プロセスを逆にする自然なプロセスです。
AddRoundKey操作は、メッセージの暗号化時と同じように、状態のすべての16バイトに対して同じ(変更されていない)S + Kiのままです。それ自身の逆です。これは、演算でXORロジックが使用され、バイトが2進数で表現できるためです。
最終ラウンドのキーは、暗号化されたメッセージに単純に追加(合計)されます。
InvSubBytes。この変換の本質は変更されていません。つまり、変換されるメッセージの各バイトは、テーブルから取得された別のバイトに置き換えられます(S -1-block)交換。もちろん、置換テーブルはここでは異なります。バイト{x、y}は、同じ原理に従って、Inv S(x、y)からのバイトに置き換えられます:x-テーブルの行、y-その列。置換バイトは、Inv S(x、y)テーブルの行(x)と列(y)の交点にあるセルから取得されます。
以前と同様に、テーブルのサイズは16×16 = 256バイトであり、それぞれがシフトマトリックスCの積からベクトルマトリックスの乗算と減算(アフィン変換)によって取得されます。バイナリフィールドでは、加算と減算の演算は同じであるため、ベクトルCを製品。 InvSubBytesテーブルを以下に示します。指定された置換のノードS -1は、次の表1に示されています。値は16進形式で示されています。
表1.逆S -1の置換のテーブル-ブロック

表は、緑で塗りつぶされた2バイト4A→5Cおよび9F→6Eの置換の例を示しています。
InvShiftRows。この変換により、テーブルの行(州の正方形)が右に(元のシフトとは逆の方向に)シフトされます。各行のシフト値は同じままです。最初の(一番上の)行はc0 = 0にシフトされず、2番目の行はc1 = 1だけシフトされ、次の行はc2 = 2だけシフトされ、最後の行はc3 = 3位置(セル)です。値c0、c1、c2、c3は、表と図の最初のラウンドのメッセージ変換で示したものです。

スカラー表現でのこのような乗算の結果は次のとおりです
。S'0C =({0l}・S0C){({0b}・S1C)⊕({0d}・S2C)⊕({09}・S3C);
S'1C =({09} S0C)⊕({0l} S1C)⊕({0b} S2C)⊕({0d} S3C);
S'2C =({0d} S0C)⊕({09} S1C)⊕({0l} S2C)⊕({0b} S3C);
S'3C =({0b} S0C)⊕({0d} S1C)⊕({09} S2C)⊕({0l} S3C)。
PCからITを取得するために、復号化アルゴリズムは、暗号化プロセスで使用されたものと同じパラメーター値を使用します。拡張キーの形成については、ルールは同じままです。
直接復号化オプション
一部の逆変換の復号化アルゴリズムの特性により、暗号化アルゴリズムと同じ一連の操作を保持できますが、一部のパラメーター値には変更が必要です。まず最初に、キー(展開)について説明します。
調査によると、SubBytes()関数とShiftRows()関数の順序は結果の値を変更しない、つまりこれらの関数は入れ替え可能(通勤)であることがわかっています。この位置(プロパティ)は、関数InvSubBytes()、InvShiftRows()にも当てはまります。このパターンは簡単に説明できます。重要なのは、どちらの関数も整数バイトで動作し、シフトはバイトの整数倍で実行され、バイト自体の値を変更しないことです。
MixColumns()操作については、次の点に注意してください。入力バイト(データ)に対して線形です。
InvMixColumns(状態XORラウンドキー)= InvMixColumns(状態)XOR
InvMixColumns(ラウンドキー)。
関数(プロパティ)のこれらの機能により、アプリケーションの順序を変更できます。つまり、
InvSubBytes(InvShiftRows())= InvShiftRows(InvSubBytes())です。
AddRoundKey(InvMixColumns())= InvMixColumns(AddRoundKey())です
が、拡張復号化キーの列(32ビットワード)が以前に
InvMixColumns()関数を介して渡されていた場合。
これは、暗号化に採用された関数の使用順序を維持することで、PCの復号方法を有効にできることを意味します。明らかに、この場合、暗号のハードウェアおよびソフトウェア実装のコストは大幅に削減されます。変更は、キー配置を生成する手順のみに関係します。
InvMixColumns()関数では、変数の型を変換する必要があります。関数の入力パラメーターは2次元のバイト配列(正方形)であり、拡張キーは32ビットワードの線形(文字列)配列として形成されます。このため、正方形への型合わせを行う必要があります。
2ラウンド変換の例を使用して、RIJNDAEL復号化手順の2つの同等バージョンを示します。最初のオプションは、暗号化関数の通常の逆です。 2番目のオプションは、3組の変換
InvShi ftRows()→InvSubBytes()で2回、
AddRoundKey()→InvMixColumns()で1回操作の順序を変更することにより、最初のオプションから取得されます。
変換の結果は、元
の操作から指定したペアの操作の逆のシーケンスに渡すときに保存されます。
この表から、暗号化手順と復号化手順の2番目のバリアントは、ラウンドキー(AddRoundKey操作を実行する場合)、置換テーブル(SubBytes()およびInvSubBytes()操作を実行する場合)、および変換行列(MixColumns( )およびInvMixColumns())。
表2-RIJNDAELの2ラウンドバージョンでの変換のシーケンス

同様の結果は、任意の数のラウンドに当てはまります。
最後のサブキーを使用して暗号キーを回復する
ラウンドAES暗号鍵の生成。 128ビットの元の暗号鍵からラウンド鍵を生成するための鍵スケジュールは、再帰的な機能です。この機能については、ここで詳しく説明します。その起動の初期条件は、キーの最初の4つの4バイトワード(4×32ビットワード)、つまりW [0]、W [1]、W [2]、W [3]です。この128ビットの暗号鍵を復元する問題を次のように定式化して
みましょう。ラウンド10のラウンド鍵W [43]、W [42]、W [41]、W [40]のコンポーネントを見つけます。
このラウンド鍵のみで完全な暗号鍵を回復する必要があります。
最初に数値データで問題の解決策を検討すると便利です。FIPS PUB 197に示されている数値の例を基に考えてみましょう。。表3には、ラウンド10キーが含まれています。
ラウンドキーを生成する手順は、以前のいくつかのキー値に沿って前方移動(キーの展開)を提供するように構成されています。一連の値のあるポイントから逆方向に移動するには、この戻りポイントで計算プロセスの初期データを取得する必要があります。戻り点を最後の10ラウンドの最後のステップとする、つまり、10ラウンドキーの4つの4バイトワードが4つわかっているNk = Nb = 4
表3-AES暗号の10ラウンドの128ビットキー

さらに、キー回復アルゴリズムの結果とアクションは、これは(一種の覆された)鍵生成テーブルに似ています。
表4-第10ラウンドの既知の鍵からの暗号鍵の回復

表4の説明。ラウンド数は、10日から1日まで逆順にカウントされます。テーブルの3列(3、8、9)には、i行番号に応じて異なる現在の番号を持つ既製のキーが含まれています。残りのセルには、中間計算のための補助データが含まれています。したがって、キーW [i]の値は、3つの列で3回表に表示されます。
列1および2は、ラウンドの番号rと4バイトのキーワードの序数iです。暗号化中の最後のそのような単語の番号はi = 43です。表では、右側(9)列の一番上の行にそれを書き込みます。テーブルの行の番号iは減少しており、列9では、キーW [i]の単語に対応しています。 8列目には、キーの単語W [i-Nk]が含まれ、数字が減少したW [43-4] = W [39]、3列目にはキーワードW [i-1] = W [42]、以前のW [i] = W [43]。
8列目のW [39]の意味は不明であり、式を使用して初期データからそれを見つけます
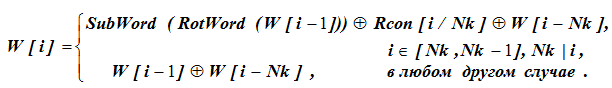
。式の計算では、式の線を選択するための条件が最初にチェックされます。 W [43]の場合、i = 43であり、Nkは値43を完全に除算しません。つまり、i = 43の場合、W [i]の値は式の一番下の行によって決定されます。W[43] = W [42] W [39]。ここで、W [42]およびW [43]の所定の値について、最後の項W [39]は定義されていません。
次に、W [39] = W [43] W [42] = b6630ca6-e13f0cc8。
2進算術mod2では、加算と減算の演算は同等であるため、キーワードW [39]の4バイトごとのビットごとの計算は、次の形式になります(表5)。
表5-キーワードWのバイト計算[39]。

したがって、キーワードW [39] = 575c006eの値が見つかりました。この値を3番目の列、i = 40行、9番目の列にi = 39
行に転送します。i= 40行の計算は、キーを展開するときと同じように実行されます。
未知の単語W [i-Nk] = W [40 –Nk] = W [i = 36]は、前のケースと同様に、40行目のW [36] = W [40] 7列の差によって決定する必要が
あります。次に、7-ライン40の第3列は、第5列と第6列の合計(OR)として形成される。 5番目の列の値は、RotWord循環シフト(4番目の列)とSubWord置換演算(5番目の列)の後、W [39]から取得されます。
これらのアクションの結果は、
RotWord(575c006e)= 5c006e57の形式になります。 SubWord(5c006e57)= 4a639f5b。
6列目の値は定数として取得されます
Rcon [j = i / Nk] = Rcon [j = 40/4] = 2 j-1 = 2 9。
この定数はバイトの16進数で表される
2 9 ≈100000000= X 9が、そのようなバイトが存在しないGF(2 8)フィールド:既約多項式で割り算の余りを求める必要がある、すなわち
キーワードに定数を含めた後、
Rcon [j = 40 / Nk] = 36000000(6列目)になります。 7列目の値は、(7列)=(5列)⊕(6列)=4a639f5b⊕36000000= 7c639f5bの形式で取得されます。
そして最後に、
W [36] = W [40](行40の7列目)= d014f9a8 7c639f5b = ac7766f3です。
類推によるさらなる計算は、最終的な結果である暗号キーにつながります。
wおよびRotWord、Rcon、SubWord関数の詳細情報があります。ドキュメントのように、Kr [j]-r番目のラウンドキーのj番目のバイトとw [i]で示したとします。
Kr =(w [Nk∙r]、w [Nk∙r + 1]、・・・、w [Nk∙r + Nk-1])が得られます。
異なるiの場合
、i≠0 mod Nk、Nk≤i <Nb∙(Nr +1)、w [i] = w [i-Nk] xor w [i-1]に対して次の関係があります。
for i = 0 mod Nk、w [i] = w [i-Nk] xor SubWord(RotWord(w [i – 1]))xorRcon [i / Nk]。
したがって、i≠0modNkの場合、Nk0≤i<Nb∙(Nr + 1)–Nk、w [i] = w [i + Nk] xor w [i + Nk-1]およびi = 0modNk、w [i] = w [i + Nk] xorSubWord(RotWord(w [i + Nk – 1]))xorRcon [i + Nk / Nk]
AES-256では、iが4mod Nkに相当するときにサブワード演算を追加する必要があります。したがって、最後のサブキーから前のキーを推定し、段階的に暗号キーの値K0を取得することが可能です。
AES-128暗号の数学的基礎は非常に完全であり、ここで詳しく説明します。
フィールドマッピングturnを見てみましょう。GF(2 8)→GF(2 8); x→x 2 + x。このマップの画像
1= Im(l)の次元はdim GF(2)(1)= 7です。
方程式x2 + x =θ。ここで、θ1には2つの異なる解(方程式の根)1、2єGF(2 8)があります。
ビエタの定理x1⊕x2= 1により、根の合計はx 2での方程式の係数と反対の符号で等しく、根の積x1⊗x2=θは方程式の自由項に等しくなります(反対符号のある方程式では)。
バイナリフィールドの演算では、要素mod2の加算と減算の演算は同等であることが知られています。

したがって、方程式の根は比x2 =x1⊕1によって関連付けられます。これは、方程式のxでの係数が1であるためです。これは、辞書式順序を持つフィールド要素の10進数表現では、順番に配置され、1つだけ異なることを意味します。
したがって、x = 0およびx = 1の場合、x = 2およびx = 3の場合、次のようになります。

削減されたペア(0、1)でのマッピングの結果(画像)。(2、3)完全に一致、つまり 2つのタイプが1つの画像に対応します。その結果、イメージのカーディナリティは、プレイメージのカーディナリティよりも2倍少なく、その要素の次元は7です。
根のペアの積、つまり、2次方程式の自由項は、フィールドの要素のパワー表現(逆イメージ)を使用して定義すると便利です。この場合、指数はmod255で合計されます。体GF(2 8)の乗法群の次数を法として