
どうもありがとう。ここに座ってごめんなさい。私はとても老人です。
今日の私のトピックは、非常に古くからある意味で非常に特別なものです。キンクは人間の生活に不可欠な部分であり、常にそこにあります。古代人はこれについて書いた。このことは主に私たちのコントロールの外にあります。そして、ある意味で、それらは非常に複雑なものであるように見えます-完全な混乱です。
障害には多くの種類があります。だから偶然にも、何年も前に私はこの形の合併症に対処し始め、そして驚いたことに、私は兆候を発見しました。それでは、今日、これが何を意味するかについていくつかの例を紹介したいと思います。ラテン語を勉強した人は、遠い青年期の私と同じように、「むら」よりも「壊れた」という言葉を好みます。しかし、これはそうではありません。
平等は骨折の反対です。なぜなら、ほとんどの世界は骨折に満ちているように見えます。
いくつかのオブジェクトを紹介します。それらのいくつかは人工的に作成されます。他のものは、ある意味で非常に現実的です。これは本物です。

これはカリフラワーです。なぜ私はあなたに普通で古代の植物であるカリフラワーを見せているのですか?なぜなら、そのルーチンと古さにもかかわらず、複雑でシンプルだからです。複雑でシンプルです。例えば、それを計量することは難しくありません。私たちがそれを食べるつもりなら、重量が重要です。しかし、その表面を測定するとします。これは面白くなってきています。カリフラワーの花の1つを鋭利なナイフで切り取り、よく見ると、カリフラワー全体が小さく表示されています。その後、何度も何度も何度もカットすることができます...そして、カリフラワーの標本がますます小さくなります。人間の経験では、各部分が全体に似ているがサイズが小さいほど興味深い特性を持つフォームがあることが示されています。そして、その人はこの事実から何を学びましたか?ほんの少し。
この問題の研究に関連して、私は完全に驚くべき何かを発見しました。キンクは、たとえば2.3または1.2、そして時にはそれ以上の数で測定できます。ある日、友人が写真を持ってきて、冗談半分で「この曲線のねじれは何ですか?」と尋ねました。私は、「1.5未満と少し」と言いました。結局のところ、それは1.48に等しかったです。これらのことを長い間研究していたので、それほど長くはかかりませんでした。問題の数値は、表面の破損の程度を示します。

表面は完全に人工であり、コンピューター上で作成されたものであることをすぐに予約しておきます。唯一の出発点は数でした。この数はキンクです。左側のフラクチャは、いくつかの風景からのコピーの結果です。右側-自分でより高いキンクを設定します。よく見ると、しばらくすると肉眼でこれら2つのケースの違いを確認できます。
人は骨折の概念に慣れなければなりませんでした。これは非常に壊れていますが、これはスムーズだと言えるかもしれませんが、これは完全にスムーズです。非常にスムーズなものはほとんどありません。それでは、カリフラワーの表面は何ですか?それは測定することができ、測定して測定することができます...測定がより正確であるほど、表面は大きくなり、非常に短い距離まで続きます。これらの湖の海岸線の長さはどれくらいですか?測定が正確であるほど、結果は長くなります。しばしば引用されるため、海岸線の長さの概念は非常に明白に見えますが、実際には完全に間違っています。単にそのようなことはありません。別のアプローチが必要です。
そして、この知識の用途は何ですか?驚くべきことに、多くの利点があります。そもそも、私が発明した人工風景は、常に映画撮影で使われています。遠くに山が見えます。それは山であるかもしれませんが、それはちょうど流れる数式であるかもしれません。これは非常に簡単に実現できます。以前は時間がかかっていましたが、今はほんのささいなことです。こちらをご覧ください。これは本当の光です。
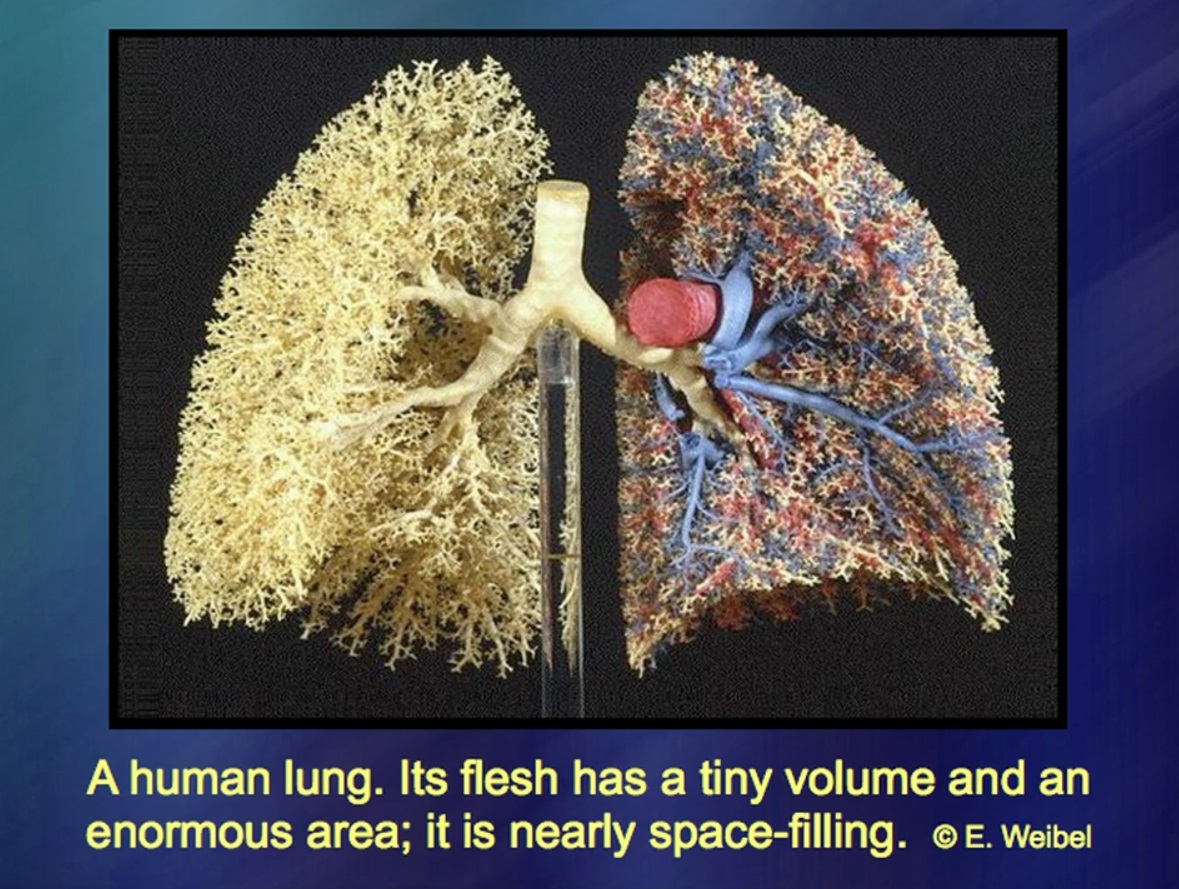
肺は非常に奇妙な物体です。私たちは皆、それがある程度の重みを持っていることをよく知っています。肺の容積が非常に小さいことも知られています。肺領域はどうですか?解剖学者たちはこの問題について長い間議論してきました。正常な男性では、肺の面積は1つのバスケットボールの面積と等しいと考えられています。他には、そのようなボールは5つないと主張しています。不一致は巨大です。どうして?肺の面積は非常に漠然と定義された概念だからです。気管支の枝と枝がどんどん深くなります。そして、彼らはいくつかの原理のためではなく、肺の内部の粘液のために、純粋に物理的な状態のために分岐を停止します。これは、はるかに大きな肺が形成される方法です。気管支はどんどん深く分岐しますが、それらの間のギャップは、クジラ、人、および小さなげっ歯類ではほぼ同じです。
これの用途は何ですか?驚くべきことに、驚くべきことに、解剖学者は最近まで肺の構造をよく理解していませんでした。驚くべきことに、私の数学的研究は、肺疾患だけでなく肝疾患も研究する外科医にとって大きな助けとなったと思います。つまり、独自のジオメトリがないものに対してジオメトリを作成する必要がありました。驚くべき品質が見つかりました:多くの場合、このジオメトリのルールは非常に簡潔です。あなたは短い式から始めて、それらを数回、時には繰り返し、何度も繰り返し適用します。同じ繰り返し。そして最終的には、そのようなことが判明します。
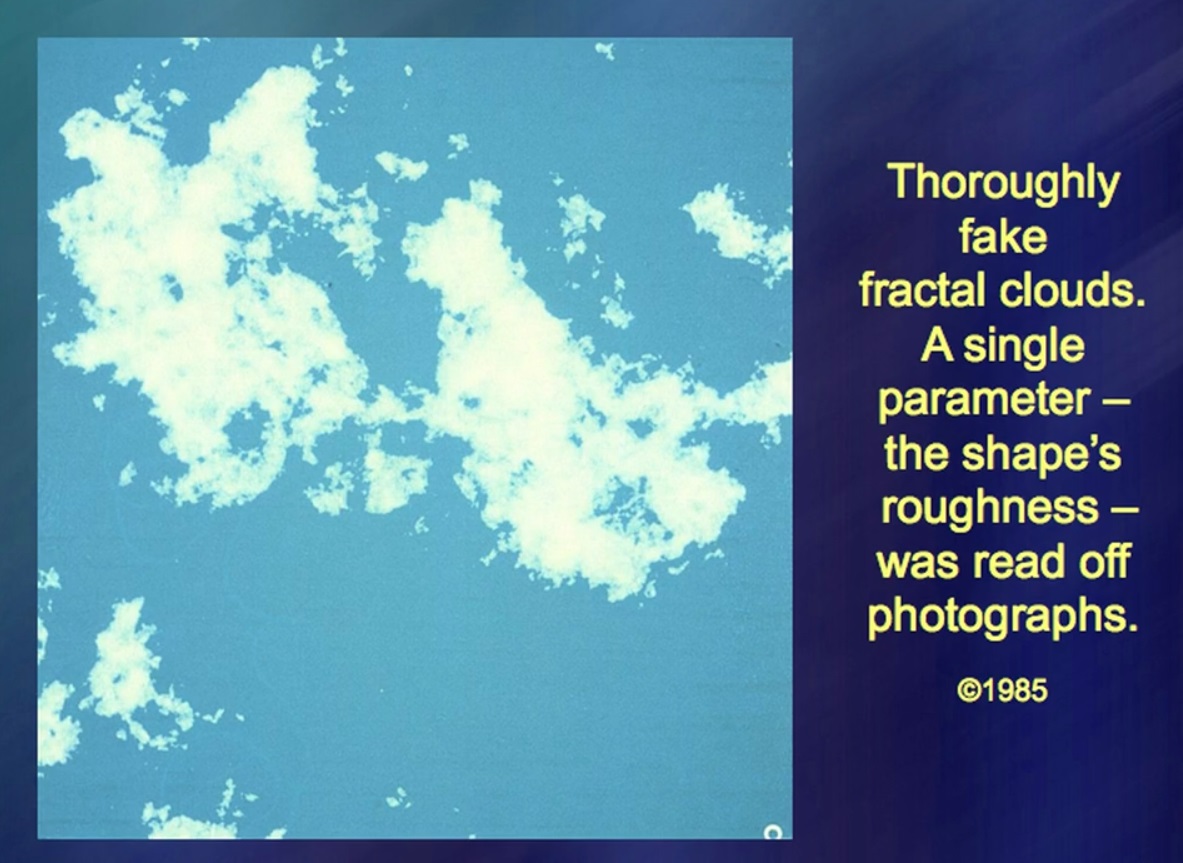
この雲は100%完全に人工です。はい、99.9%です。ここでの唯一の自然な要素は、雲の割れ目である数です。この数は自然から取られます。雲のように複雑で、不安定で変化しやすいため、単純なルールに従います。この単純な規則は、曇りを説明するものではありません。しかし、雲の海はこのルールを考慮に入れなければなりません。私はこれらの古い写真がどれほど完璧であるか知りません。私はこれを集中的に行いましたが、私の注意は他の現象に向けられました。
そして、もう1つ興味深い点があります。数学の歴史の中で革命的な出来事の1つは、多くの人には十分に評価されていませんが、約130年前、145年前に起こりました。数学者たちは存在しない形を作り始めました。数学者の間で評価され始め、想像を絶するほどの程度まで、自然が存在しなかった何かを作成する人の能力。特に、平面全体を最後の点まで満たす曲線を作成することができました。曲線は曲線であり、平面は平面であり、2つは互いに適合しません。彼らは一緒に合うことがわかりました。
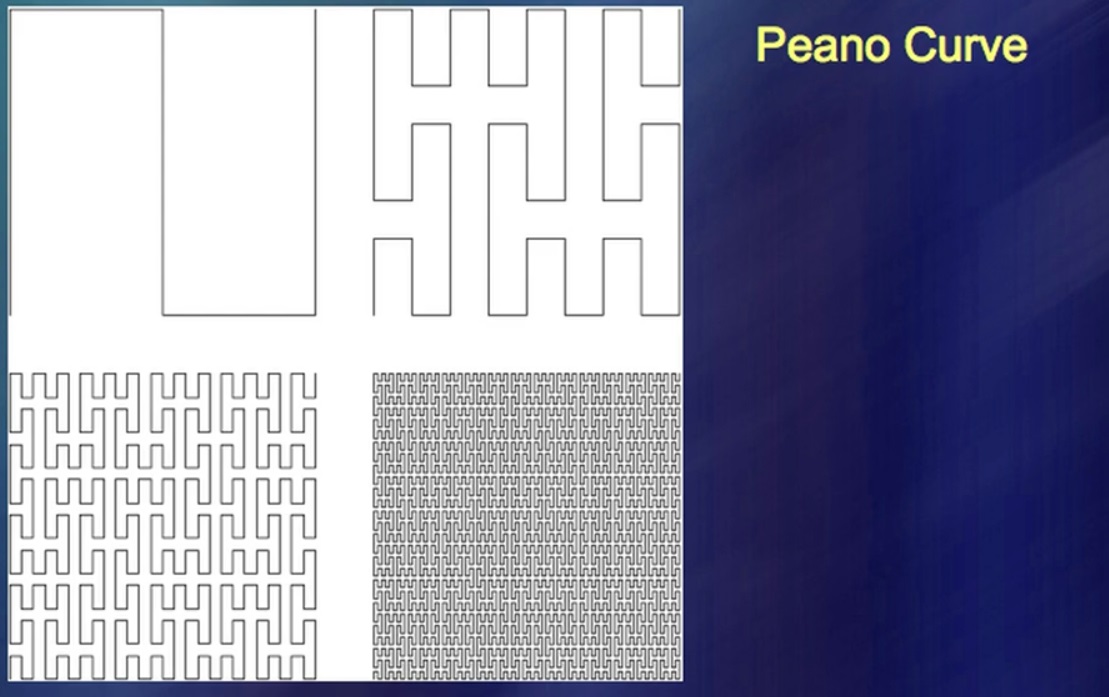
ペアノという名前の男がそのような曲線を特定し、それらは非常に興味を起こさせました。現実に基づくものと純粋な理由に由来するものに数学のある種の分割があったので、それらは大部分において非常に重要で刺激的な興味です。残念なことに、私はたまたま純粋な理由の努力によって知られるようになったことが実際には別の形で知られていることを証明しました。ここでは、平面を満たす曲線の形の細流のシステムがあります。

それ自体が歴史です。 1875年から1925年の間に、数学が現実世界から脱却する準備をしていた驚くべき時期でした。子供の頃から学生時代、数学と目に見える現実の間のギャップから、特定のオブジェクトがギャップのイラストとして機能しました。しかし、私はそれらを再考し、逆さまにし、自然の複雑さのいくつかの側面を説明する助けを借りてなんとかしました。
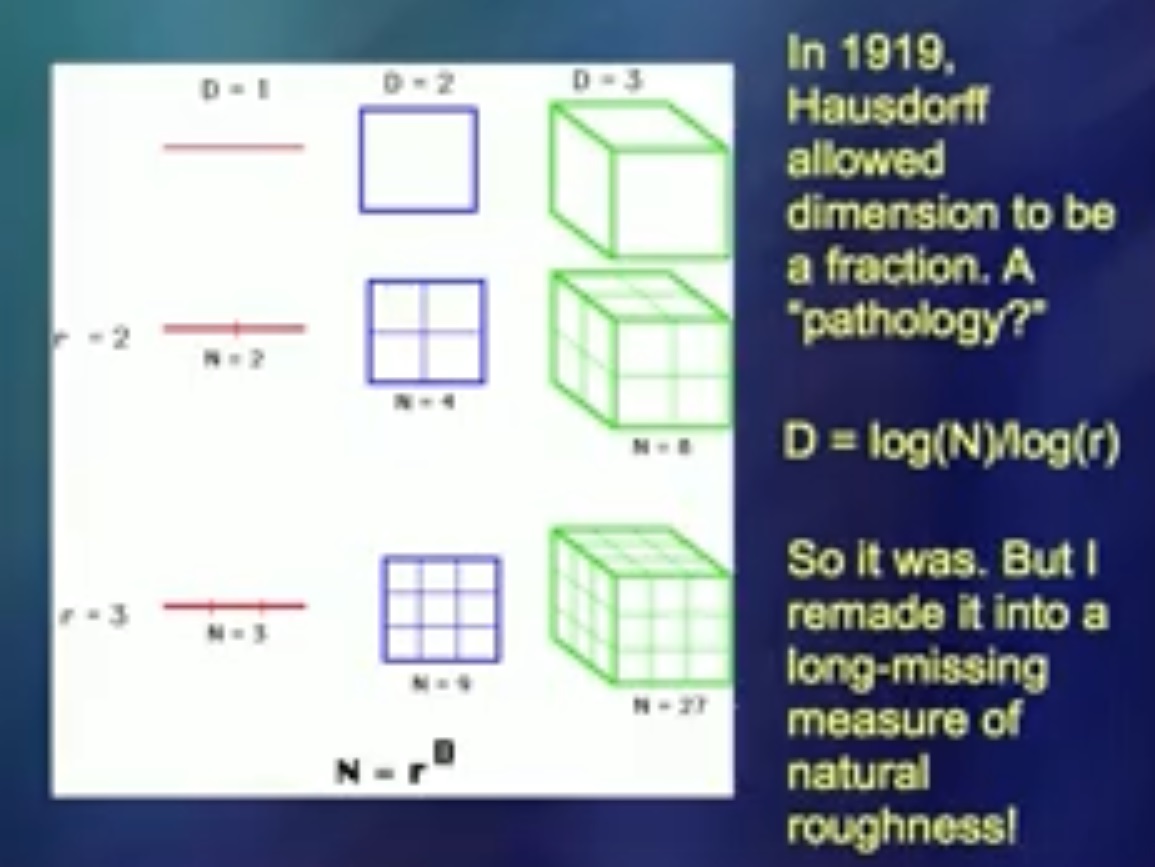
1919年、ハウスドルフという男が、数学的冗談と見なすことができる数を特定しました。しかし、私はこの数値がキンクを測定するための優れたツールであることを発見しました。私が初めてこれについて同僚に話したとき、彼らは言った、「ばかげたことはありません。これは何か…」実は私はバカなことはしていませんでした。

偉大な芸術家、北斎はこれをよく知っていました。写真の下は藻です。北斎は必要な数学を知りませんでした。それは当時存在しなかっただけです。しかも日本人だったので、当時は西洋とは連絡がありませんでした。しかし、芸術には長い間フラクタル要素が含まれてきました。私はこれについて長い間話すことができます。

エッフェル塔にはフラクタルの要素があります。私は彼の塔に関するエッフェルの本を読みました-彼の理解の範囲は素晴らしいです。
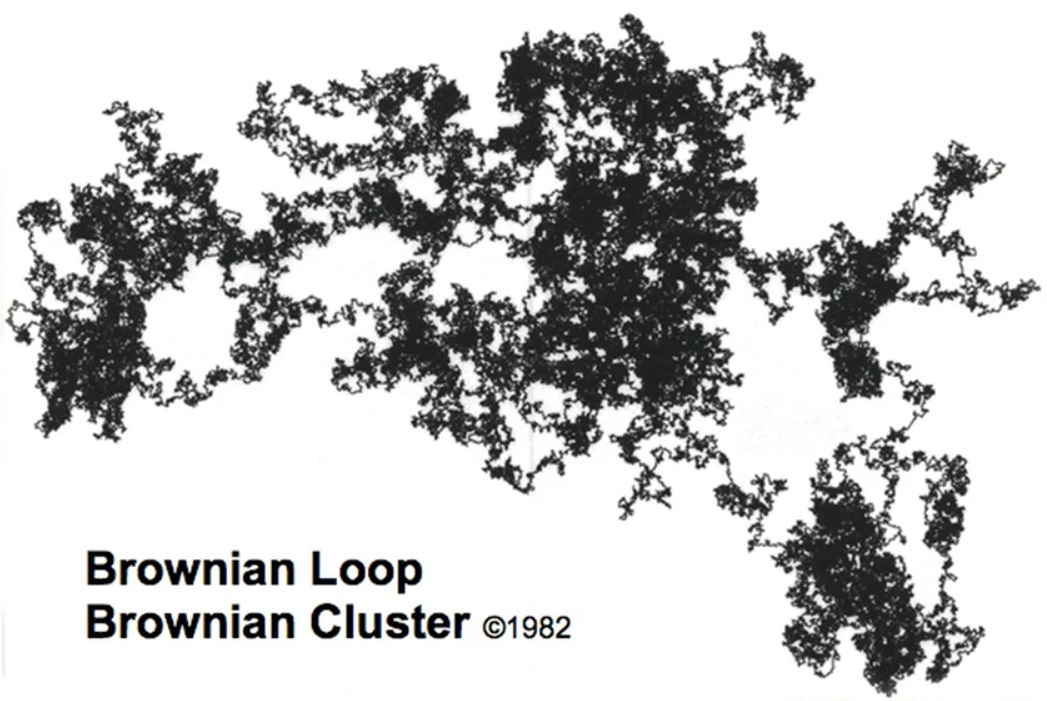
これは混乱の中の混乱です。ブラウンループ。私は自分の職業生活のかなりの部分を経験したと決心し、非常に多くの異なることが私を占めていたので、自分自身をテストする時だと決心しました。誰もが長い間探索してきた物体を探索して、そこに根本的に新しい何かを見つけることはできますか?私はブラウン運動の範疇に入るすべてのものを研究し始めました。私はさまざまな角度を試し、さまざまな方法を試し、最初の場所に戻りました。次に、アシスタントに提案しました。「ここには何も表示されません。塗り直せますか?」彼はそうしました、つまり、彼はすべての内部を満たしました。 "私はなんとかした…"

しかし、私は叫びました。やめる!やめる!了解:これは島です。」すごい。ブラウン運動は2に等しいキンクを持っています。私はそれを測定し、それは1.33と判明しました。私は何度も測定します。長い測定値、大きなブラウン運動。もう一度:1.33。数学的問題がすぐに発生します:それをどのように証明するのですか?友達に20年かかった。 3つには不完全な証拠があった。彼らは力を合わせ、一緒に証明を得ることができました。その結果、彼らは数学者に有名な[フィールズ]メダルを授与されました。全体として、数学者は私が見たが証明できなかった事実を証明するために3つの[Fields]メダルを受け取りました。
今、人々はどこでも私に尋ねます:あなたの研究はどのようにしてあなたをそのような変わったことに導いたのですか?」
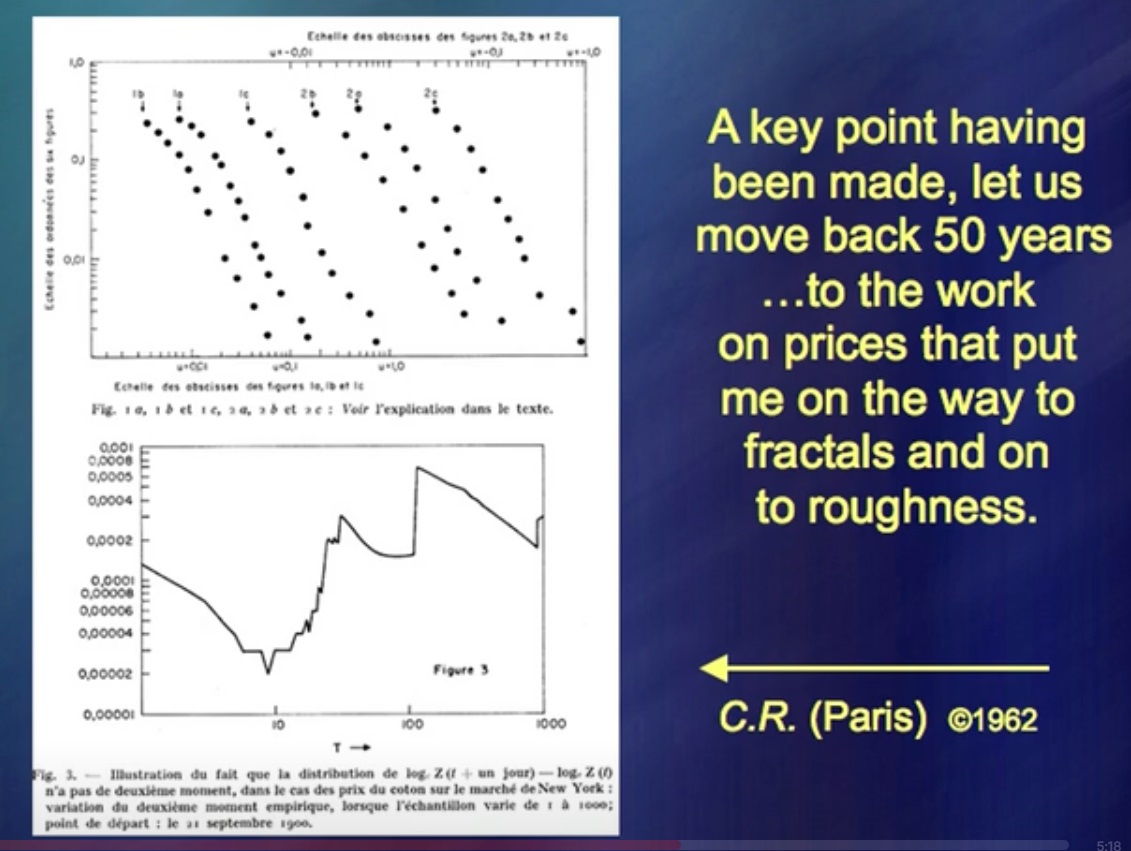
機械工学者、地理学者、数学者などを兼任できるようになったのはなぜですか。奇妙なことに、私は株式市場の価格を研究することから始めました。

理論があり、それについて本を書きました。
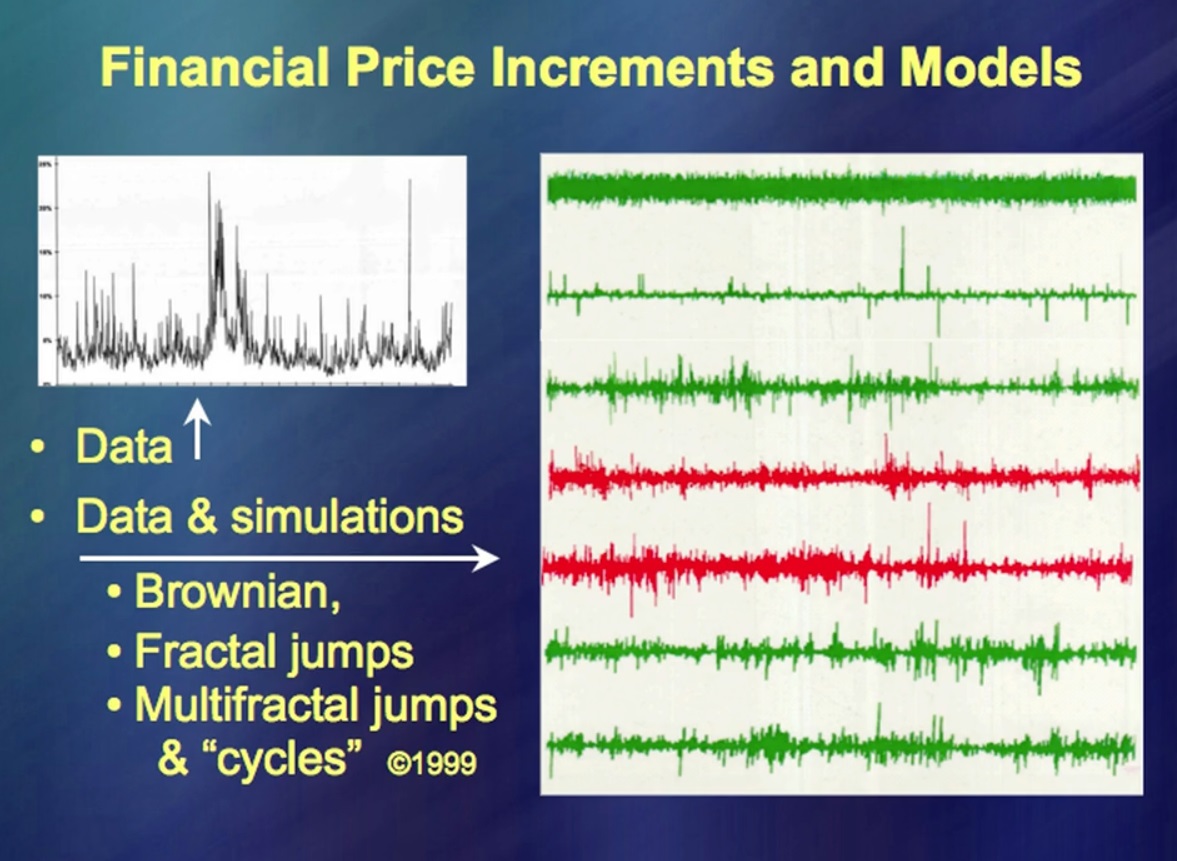
「金融商品の価格変動」左側には長期間のデータ、右側には上部に、非常にファッショナブルな理論によるデータが表示されます。それは非常にシンプルであり、あなたはそれについて多くの本を非常に速く書くことができます。 (笑い)このトピックについては何千もの本があります。次に、実際の価格変動と比較します。そして、彼らはどこにいますか?追加の行には、実際の価格変動だけでなく、私の側の小さな偽物も含まれます。主なアイデアは、あなたができるようにする必要があるということでした...それは何と呼ばれていますか? …価格変動のシミュレーション。これは50年前にうまく機能しました。
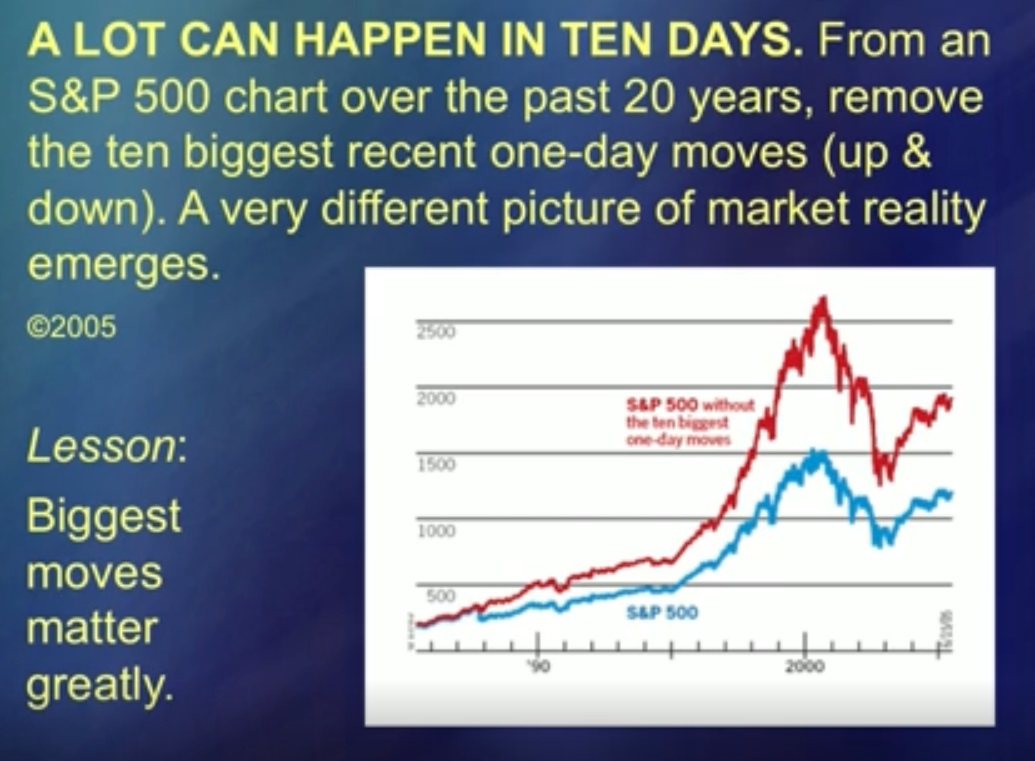
50年間、もっと簡単にできたのではないかと思っていました。しかし今、私はあなたに言います、彼らは私に耳を傾け始めました。 (笑)これらの2つの曲線は平均を表しています。青はスタンダードアンドプアーズ[S&P 500]で、赤はスタンダードアンドプアーズから、最大の5つの価格スパイクを差し引いたものです。飛躍は確かに分析を台無しにし、多くの研究ではそれは[非分析]特別なケースと考えられています。 「信じられないほどの偶然、主の介入。まあ、ささいなこと、それを脇に置くことができます。」このグラフでの主の介入は、実際には5つあり、他のすべてと同じくらい重要です。言い換えれば、主の介入を無視することはできません。
それは存在であり、まさに分析の対象です。それらに対処すれば、価格変動にも対応できます。しかし、ジャンプを把握していないので、いわゆるノイズを好きなだけ分析できますが、この分析は意味がありません。これらの曲線は影響を示しています。

次に、最後のトピック-私にちなんで名付けられたセットに移ります。ある意味、これは私の人生の物語です。私の思春期は、その頃ドイツに占領されていたフランスで過ごしました。いつのまにか自分がいないのではないかと思ったので、大きな夢を見ました。戦後、おじさんに再会しました。私の叔父は優秀な数学者で、彼は言った。 25年前、私はそれを解くことができず、誰もそれを解くことができませんでした。これは、ガストンジュリアという名前の数学者とピエールファトゥーという名前の別の数学者の構成です。ここで何か新しいものを見つけることができるなら-何でも-あなたのキャリアが確保されていることを考慮してください。」とても簡単です。私はこの問題を研究し始めました、そして私の前にそれをしようとした何千人もの人々のように、何も達成しませんでした。
しかしその後、コンピュータが登場しました。そして、私は計算能力を、たとえばこの曲がったもののような新しい数学の問題ではなく、古い問題に適用する必要があると判断しました。そして、私はいわゆる実数から切り替えました。直線上の点から複素数まで、これらは平面上の点、つまりこの問題で必要なものです。結果はそのような図です。

これは非常に複雑です。方程式はその中に隠されています。zはz ^ 2 + cに変換されます。とてもシンプルで退屈なので、面白くない。では、1回、2回実行してみましょう... 2回で十分です。奇跡について!これが表示されます。ここではこれらのことを説明するつもりはありませんが、これは何であり、これは何であることがわかります。


そのような複雑さ、調和、美しさの数字は、何度も何度も何度も繰り返し得られます。私の主な発見は、これらの島々が全体像とほぼ同じ形であることでした。結果はそのような見事なバロック様式の宝石です。

そして、すべてが含まれているこの短い式のすべて-どのくらいありますか? -5つのアイコン。そして、これが結果です。

色が追加された理由は2つあります。第一に、数字が非常に複雑であるため、数字の意味がわかりにくいためです。そして、それらを平面に反映させるために、ある種のシステムを選択する必要があります。したがって、私は原則として、常に異なる色で数字を表現することを考えました。1つの色はあるものを意味し、別の色は別のものを意味する、など難しいです。
1990年、私は英国のケンブリッジにいて、大学から賞を受賞しました。3日後、フィールドの上を飛んでいた1人のパイロットがこれを見ました。

そのようなことはどこから来るのでしょうか?もちろん-エイリアンから。
ケンブリッジの新聞の1つがこの「発見」についての記事を発表し、翌日には5,000通の手紙が届きました。これはマンデルブロのセットで、非常に大きいとのことです。

終わらせてください。この写真は純粋な数学を通して得られました。単純なルールは、無限に繰り返された場合、底のない奇跡を作成できます。
ナミク・カスモフ
による翻訳エカテリーナ・ツヴェトコワによるレビュー

SkillFactoryの有料オンラインコースを受講して、スキルと給与の注目の職業をゼロから取得する方法の詳細をご覧ください。
- Machine Learning (12 )
- Data Science (12 )
- (9 )
- «Python -» (9 )