新しい幾何学的視点が古い長方形の問題の導入を支援

検疫に退屈したジョシュアグリーンとアンドリューロブは、長方形のペグの定理の変形の1つを証明する方法を見つけました

すべての種類の長方形を閉ループで見つけることができますか？



3月中旬、数学者のジョシュアグリーンとアンドリューロブは似たような立場にあり、4つの壁の中に閉じ込められ、成長しているコロナウイルスの流行に適応しようとしました。彼らは彼らの研究を掘り下げることによってそれに対処することに決めました。



「パンデミックはこのプロセスの何らかの触媒だったと思います」とボストン大学のグリーン教授は語った。 「私たちをサポートできる何らかの共同作業を行う方がよいと判断しました。」



2人の友人が取り組むことを決めた問題の1つは、100年以上答えられなかった幾何学的な質問の変形でした。



「このタスクは、公式化して理解するのは非常に簡単ですが、解決するのは非常に困難です」-と述べましたワシントンのエリザベス・デンとリー大学。



すべてが閉じたループで始まります-始点と終点が同じカーブしたパス。GreenとLobbが引き受けたタスクは、基本的に、そのようなパスには、任意の比率の長方形の頂点を構成する4つのポイントのセットがあると主張しています。



そして、この「長方形のペグ問題」は、定規とコンパスを持つ高校生なら誰でも扱える質問のように聞こえますが、何十年もの間、数学者の最も根強い試みに抵抗してきました。そしてグリーンとロブが引き継いだとき、彼らは他に何かを期待する理由がありませんでした。



グリーンは、彼が取り組んだすべての困難なプロジェクトの中で、「これは私の意見では最も有望ではなかった」と語った。



しかし、パンデミックは拡大し、イギリスのダーラム大学と沖縄科学技術大学院大学でそれぞれ働いているグリーンとロブは、毎週ズームの会話をし、すぐにいくつかのアイデアを生み出しました。そして5月19日、世界の多くの地域が再開したとき、彼らは決定を発表しました。



長方形が実際に見つかる可能性があることを示す彼らの最終証明は、この問題を完全に異なる幾何学的レベルに持っていきます。そして、この頑固な質問は非常に簡単に当てはまります。



「それはかなり奇妙だ」とブラウン大学のリチャード・シュワルツは言った。「このアイデアはこの仕事にぴったりだった」

長方形を再考する

長方形ペグの問題は、1911年にドイツの数学者OttoTöplitzが提起した問題と密接に関連しています。彼は、任意の閉じた曲線上に4つの点があり、それらを結ぶと正方形が得られると予測しました。 「スクエアペグ」についての彼のこの質問は未解決のままです。



「これは、どのようにもハッキングすることができない古くてイライラする仕事です」とグリーンは言いました。



問題の複雑さを理解するには、四角いペグ問題で考慮される曲線の特性を知ることが重要です。これは、グリーンとロブの証明にも重要です。



このカップルは、「連続」と「滑らか」の両方の閉じた曲線の問題を解決しました。連続性とは、切れ目がないことを意味します。滑らかさは、連続性があり、コーナーがないことを意味します。紙と鉛筆で机に座っていると、滑らかで連続的な曲線を描く可能性があります。グリーン氏は「使いやすい」と語った。



滑らかな連続曲線は、単純な連続曲線とは異なりますが、正方形のペグのテプリッツ予想に含まれる曲線など、滑らかな曲線とは異なります。このような曲線には、コーナー（曲線が突然逸脱して別の方向に進む点）がある場合があります。多くの角度を持つ曲線の1つの主要な例は、雪片のようなフラクタルKoch曲線です。、実際には、いくつかのコーナーで構成されています。 Kochスノーフレークおよびその他の類似の曲線は、代数的方法を使用して分析できないため、研究が特に困難になります。



「いくつかの連続した（滑らかではない）曲線はただうんざりしている」とデンは言った。



それでも、GreenとLobbによって解決された問題は、滑らかな、したがって連続した曲線に属します。そして、正方形を形成するそのような曲線上に常に4つの点があるかどうかを判断する代わりに-滑らかな連続曲線の場合、この問題は1929年に解決されました-彼らは別のことを研究しました：特定の長方形を形成するような曲線上に常に4つの点があるかどうかプロポーション、つまり任意のアスペクト比で。正方形の場合、この比率は1：1で、高解像度テレビの場合-16：9です。







長方形のペグ問題の最初の大きな進歩は、1970年代後半にハーバート・ヴォーンによって発見された証拠でした。それは長方形の幾何学を見る新しい方法を提供し、グリーンとロブを含む他の数学者によって後で使用されたいくつかの方法を提供しました。



「誰もがこの証拠を知っています」とグリーンは言いました。 「それはほとんど民俗的で、夕食の席ですべてについて話し合うことによってそのようなことについて学びます。」



ヴォーンは、長方形を4つの接続された点として想像するのではなく、相互に関連する2組の点として想像しました。







頂点がABCDの長方形を想像してください。その中で、（対角線上の）点AC間の距離は、（他の対角線上の）点BD間の距離に等しい。また、これらの対角線はちょうど真ん中で交差します。



したがって、閉ループで長方形を検索する場合、中央で交差する同じ線分の端にある点のペアを検索できます。それらを見つけるには、それらを説明する体系的な方法を考え出すことが重要です。







これが何を意味するかを理解するために、もっと簡単なものから始めましょう。数直線を取りなさい。その上で2つの点（たとえば、7と8）を選択して、それらを数値平面（7、8）上の1点として構成します。同じ数字のペアであるポイントを作成することもできます（7、7​​）。次に、数直線上にある可能性のあるすべての可能な数のペアを検討してみましょう（それらの数は多数あります！）。そのような数値のすべてのペアを作成すると、数値平面全体が埋められます。これを表現するもう1つの方法は、数値平面が「パラメータ化」する、つまり、番号ライン上のすべての数値ペアを順番に収集することです。



ヴォーンは閉曲線上の点のペアで同様のことをしました。それは、一次元の数直線と同様に、それ自体にのみ閉じます。彼は、曲線でポイントのペアを取り、それらから図を構築する場合（そして、どれがx座標でどれがy座標であるかは問題ではない）、平面は機能しないことに気付きました。代わりに、予期しない図が表示されます- メビウスの帯、片側だけの2次元の表面。







そして、ある意味で、これはかなり論理的です。理由を理解するには、曲線上の点のペアを選択し、それらにxとyという名前を付けます。次に、xからyに移動し、曲線の一部に沿って移動します。同時に-yからxに移動し、反対側に移動します。このプロセスでは、順序付けられていないペア（x、y）で開始および終了する、曲線上のポイントのすべてのペアを通過します。しかし、これはあなたを最初に戻します-ポイントの最後のシーケンスだけが最初のものと反対になります。方向を反対に変える無秩序な点のループがメビウスの帯の本質です。



このリボンは、長方形のペグ問題の一部として分析できる新しいオブジェクトを数学者に提供します。ヴォーンはこの事実を使用して、どの曲線にも、正方形を形成する4つの点のセットが少なくとも1つあることを証明しました。

4次元の回答

グリーンとロブの証明はヴォーンの研究に基づいています。ただし、いくつかの追加の調査結果も組み合わされ、その一部は比較的最近のものです。最終証明は正確な道具のようなものであり、その望ましい結果は慎重に考慮されたアイデアの組み合わせに依存します。



彼らの証明の最初の主要な要素の1つは、プリンストン大学のPhDの学生であるコールヒューゲルマイヤーが論文を発表した2019年11月に発表されましたヴォーンが使用したメビウスの帯を分析する新しい方法を示す。これは、ネストと呼ばれる数学的プロセスを使用しました。これは、オブジェクトを取得して幾何学的空間に投影するときです。その結果、グリーンとロブはヒューゲルマイヤーの技術を取り入れ、それを別の幾何学的空間に移しました。しかし、彼らが何をしたかを理解するには、まず彼が何をしたかを理解する必要があります。



ネストの簡単な例を次に示します。



1次元の線から始めましょう。直線の各ポイントは、1つの数値で定義されます。次に、この線を2次元空間に埋め込みます。つまり、平面上に描画します。



xy平面に直線を埋め込んだ後、その各点は2つの数値（x座標とy座標）によって既に決定されています。これらの座標は、点が平面上のどこにあるかを表します。これで、2Dジオメトリテクニックを使用してラインを分析できます。



ヒューゲルマイヤーのアイデアは、メビウスの帯のようなものを取ることでしたが、それを4空間に埋め込むことで、4次元ジオメトリのプロパティを使用して、目的の結果を証明できます。



「基本的に、メビウスの帯があり、各点に4つの座標を割り当てる必要があります。それは、4次元空間内の点のアドレスのようなものになるでしょう」とロブは言いました。



Hugelmeyerは、これらのアドレスを、曲線上の長方形を見つけることで、主な目標に到達しやすいように割り当てました。彼は、住所、州、都市、通りの名前、家の番号など、曲線上の各ポイントに割り当てたと言えます。



これを行うために、彼はメビウスの帯の特定の点から始め、彼女が示した元の閉じた曲線の2つの点を取った。次に、これらの点を結ぶ線分の中点を見つけ、そのx座標とy座標を決定しました。 4次元の住所（州と都市）の最初の2つの値を取得しました。



次に、曲線上の2つの元のポイント間の距離を測定しました。この長さは、4次元の住所（ストリート名）の3番目の値になります。最後に、元の2つの点を結ぶ線分とx軸の間の角度を計算しました。この角度は、4次元の住所（家番号）の4番目の値になりました。これらの4つの値は、カーブ上のポイントのペアに関するすべてを伝えます。







この演習は十分に難しそうに聞こえますが、すぐに報われました。ヒューゲルマイヤーは付属のメビウスの帯を持って向きを変えました。回転したメビウスの帯が元の位置に対して相対的に移動し、帯の2つのコピーが交差します。ターンは4次元空間で行われたため、メビウスの帯の自己交差形状は想像するのが困難ですが、数学的に説明するのは簡単です。



この交差点は非常に重要でした。メビウスの帯の2つのコピーを互いに重ね合わせると、元の閉じた曲線上に2組の点が見つかり、長方形の4つの頂点が形成されます。



どうして？



まず、長方形は、同じ長さのセグメントの共通の交点の中心を結ぶ2組の点として表現できることを覚えておいてください。ネストされたメビウスの帯の各ポイントに割り当てられた4次元アドレスの最初の3つの値にエンコードされているのはこの情報です。



次に、4次元空間では、メビウスの帯を展開して、4次元の住所の各ポイントの座標を1つだけ変更できます。家の番号は変わりますが、通り、都市、州は残ります。例として、レンガを手前に置き、それを右に移動すると、x座標のみが変化し、yまたはzは変化しないことに注意してください。





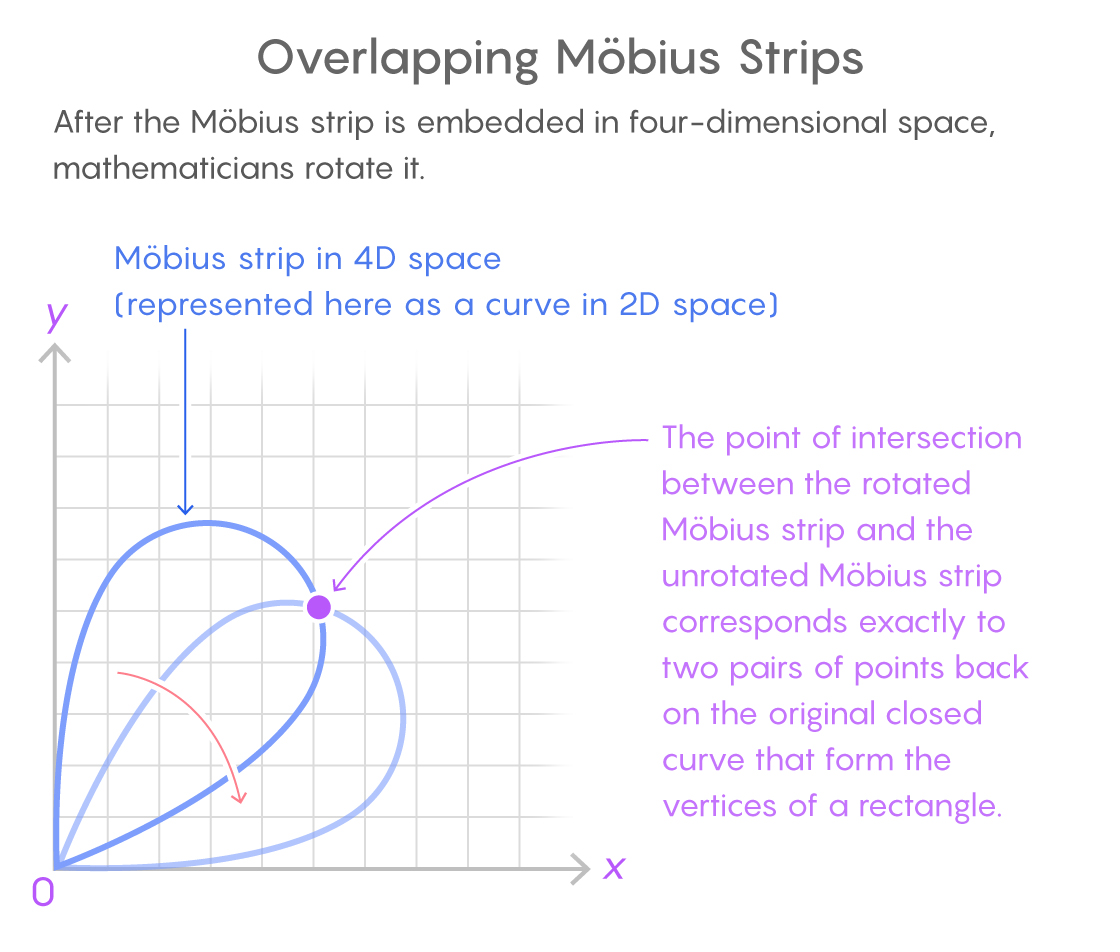
ここでは、4次元空間のメビウスの帯が2次元曲線で示されています。 2つのコピーの交点は、長方形を形成する元の閉じた曲線上の2組の点に対応します。



ヒューゲルマイヤーは、メビウスの帯を4次元空間で回転させて、ペアを結ぶ線分の中点を示す2つの座標が変化しないようにする方法を説明しました。ポイントのペア間の距離を示す座標も同様です。その回転は最後の座標のみを変更しました-ポイントを接続するセグメントが配置されている角度に関する情報が含まれています。



その結果、メビウスの帯の回転したコピーとそのオリジナルの交点は、閉曲線上にある2組の点に正確に対応し、共通の中心（それらを結ぶ線分の交点）を持ち、互いに同じ距離にあります。つまり、この交点は、曲線上の長方形の4つの頂点に対応しています。



2つのスペースの交点を使用して正しい点を見つける方法は、四角形と長方形のペグの問題の解決に長い間使用されてきました。



「これらのスペースの交差点に望ましいスペースがあります」とDenn氏は述べています。 「四角い止め釘の歴史からの多くの証拠はこの考えを持っています。」



Hugelmeyerは4次元環境で交差戦略を使用し、彼よりも前に誰よりも多くを獲得しました。メビウスの帯は0度から360度までの任意の角度で回転でき、これらの回転の3分の1が元のコピーと回転したコピーの交点になることを彼は証明しました。これは、考えられるすべての縦横比の3分の1を持つ閉じた曲線上で長方形を見つけることができると述べるのと同じです。



「メビウスの帯を4D空間に配置し、4D技術を使用することを考えたのは、コールの功績だ」とGreen氏は語った。



同時に、Hugelmeierの結果は挑発的なものであることが判明しました。4次元空間がこの問題の処理に非常に役立つ場合、なぜすべての長方形の3分の1だけに役立つのでしょうか。



「結局のところ、残りの3分の2を獲得する方法がなければなりません」とグリーンは言いました。-しかし、どうやって？」

シンプレクティックアプローチ

グリーンとロブは、パンデミックが彼らを家に送る前でさえ、長方形のペグの問題に興味を持っていました。 2月、ロブは沖縄科学技術大学院大学で会議を主催し、グリーン氏も出席しました。カップルはこのタスクについて数日間話しました。その後、東京の景色を見ながら、さらに一週間話し合った。



「私たちはこの問題について話し合うことを止めていません」とロブは言いました。 「私たちはレストラン、カフェ、美術館に行き、時々これについて考えました。」



彼らは家に閉じ込められた後も彼らの議論を続けた。彼らは、メビウスの帯を回転させると交点ができることを証明したいと考えていました。これは、任意の比率の長方形を見つけることと同じです。



4月中旬、彼らは戦略を立てました。それは、テープを特別な種類の4次元空間に埋め込むことを意味しました。通常の入れ子は、目的のオブジェクトを何らかの方法で配置することを意味します。 1次元の閉じた曲線を2次元平面に埋め込む方法がいくつあるか想像してみてください。その数は無限です。テーブルにループで結ばれたスレッドを配置する方法は無限にあるからです。



しかし、ループをネストする2次元の表面には独自の構造があるとしましょう。たとえば、地球の表面に風が吹く方向と速度を矢印（またはベクトル）で示した地図を想像してみてください。これで、各ポイントに追加情報または構造を持つ2Dサーフェスができました。



次に、制限を導入できます。1次元のRFPをマップ上に配置して、常にマップ上の矢印の方向に従うようにする必要があります。



「曲線がこれらのベクトルに従うように制限します」とシュワルツ氏は語った。これで、カーブを配置する方法が少なくなりました。







他の幾何学的空間は異なる制約を課すかもしれません。グリーンとロブの仕事にとって重要なのは、いわゆるものでした。シンプレクティックスペース。



この幾何学的な概念は、19世紀に軌道を回る惑星などの物理システムを研究したときに初めて現れました。 3次元空間を移動する惑星の位置は、3つの座標によって決まります。しかし、アイルランドの数学者ウィリアム・ローワン・ハミルトンが観察したように、惑星の運動経路の各点に、その運動量を表すベクトルを配置することもできます。



1980年代、ソビエトとロシアの数学者ウラジミールイゴレビッチアーノルド は、シンプレクティックジオメトリの研究を開発しました。彼は、シンプレクティック構造の幾何学的空間は、回転すると、そのような構造を持たない空間よりも頻繁に交差することに気づきました。



これはグリーンとロブにとって完璧でした。彼らはすべての比率の長方形ペグ問題を解決したかったので、パラメーター化されたメビウスストリップの回転コピーも頻繁に交差することを証明しました。それで彼らは二次元のメビウスの帯を四次元のシンプレクティック空間に埋め込もうと試み始めました。 「根本的に新しいアイデアは、シンプレクティックジオメトリの観点からこの問題に取り組むことでした」とグリーンは言いました。 「それですべてが変わった」



4月末までに、グリーンとロブは、メビウスの帯を4次元のシンプレクティックスペースに埋め込んで、その構造に合わせることができると判断しました。その後、シンプレクティックジオメトリツールの使用を開始できます。その多くは、自己交差の問題に直接関連しています。



「メビウスの帯がシンプレクティックの規則に従うように作れるなら、シンプレクティックの定理のいくつかを使うことができる」とロブは言った。



グリーンとロブは、フーゲルマイヤーの結果を改善できると確信していました。つまり、交差がすべてのコーナーの3分の1だけで発生していないことを証明しました。これは、曲線のポイントから、すべての可能な比率の3分の1を超える長方形を作成できることを意味します。



「このアイデアを得たとき、何かが起こることが明らかになった」とロブは言った。



ただし、結果はより一般的なものであり、予想よりもはるかに高速に表示されました。奇妙な数学的オブジェクト、シンプレクティックジオメトリのコンテキストでは1つの重要なプロパティを持つクラインボトルに感謝します。

クラインボトル接続

クラインのボトルは、モダニズムの水差しのように見える2次元の表面です。メビウスの帯と同様に、表面は1つだけで、2つのメビウスの帯を接着することで作成できます。 （多くの数学者がそうであるように）収集して机の上に置くことができるクラインのボトルは、それ自体と交差します。それが交差しないようにクラインの瓶を三次元空間に置くことは不可能です。



「クラインのボトルは表面でなければなりませんが、そのハンドルはボトルを突き破って外側から内側に移動する必要があります」とシュワルツ氏は語った。



ただし、これは必ずしもそうではありません。クラインボトルはそれ自体と交差しないように4D空間にネストできます。 4番目の次元には操作の余地があり、クラインボトルはそれ自体をバイパスできます。これは、2人が1次元の線でお互いに向かって歩いている場合、衝突を回避できないのと比較できますが、2次元の床を歩いている場合、簡単に背を向けることができます。







5月、グリーンとロブはクラインボトルについての1つの事実を思い出しました-それはそれがそれ自体と交差しないように4次元シンプレクティック空間に埋め込むことはできません[ 別のロシアの数学者、Vsevolod Viktorovich Shevchishinの仕事から]4次元空間でのクラインボトルのラグランジアン埋め込みに関する/約transl。]。つまり、シンプレクティック空間のすべての要件を満たす自己交差のないクラインボトルはありません。この事実が証明の鍵となった。 「それは魔法の杖でした」とグリーンは言いました。



そしてそれが理由です。 GreenとLobbは、メビウスの帯を4次元のシンプレクティック空間に埋め込んで、彼の要件を満たすことができることをすでに示しています。メビウスの帯の各ターンが元のコピーと交差するかどうかを知るだけでよい。



ただし、交差する2つのメビウスの帯は、そのような空間で交差するクラインの瓶に相当します。そして、回転したコピーがオリジナルと交差しないようにメビウスの帯を回転させると、それ自体と交差しないクラインの瓶ができます。しかし、そのようなクラインボトルは4次元のシンプレクティック空間には存在できません。したがって、ネストされたメビウスの帯の可能な回転もそれ自体と交差する必要があります。つまり、閉じた滑らかな曲線ごとに、任意の比率の長方形を形成する4つの点が見つかります。



証明の終わりは、雪崩のように読者を襲います。



「それは最初にセットアップされ、セットアップされ、セットアップされ、それからうなり声が出て、証明の準備が整います」とDenn氏は述べています。



GreenとLobbの証明は、問題の解決が適切な視点の発見にどのように依存するかを示す良い例です。世代の数学者たちは、このバージョンの長方形のペグ問題に取り組むことができませんでした。なぜなら、彼らはより伝統的な幾何学的条件でそれを解決しようとしたからです。グリーンとロブが問題をシンプレクティックの世界にもたらしたとき、それは簡単に解決されました。



「これらの問題は、1910年代と1920年代に発生しましたが、それらを反映する適切なプラットフォームがありませんでした」とGreen氏は述べています。「そして今、私たちはそれらが実際、シンプレクシティーの現象の隠された化身であることを理解し始めています。」