出典：unsplash.comは

ジャッキー・スチュワートによると、3度のフォーミュラ1世界チャンピオンは、車を理解することは、彼はより良いドライバーになって支援してきました：「レーサーはエンジニアが、なくてもかまいません力学への関心。」

Martin Thompson（LMAX Disruptorの作成者）はこの概念をプログラミングに適用しました。簡単に言えば、基盤となるハードウェアを理解することで、アルゴリズムやデータ構造などの設計に関するスキルが向上します。Mail.ruクラウドソリューション

チームは、プロセッサの設計をさらに掘り下げた記事を翻訳し、CPUの概念のいくつかを理解することで、より適切な意思決定を行う方法を検討しました。

基礎

最新のプロセッサーは、対称型マルチプロセッシング（SMP）の概念に基づいています。プロセッサは、2つ以上のコアが共通のメモリ（メインまたはランダムアクセスメモリとも呼ばれる）を共有するように設計されています。

さらに、メモリアクセスを高速化するために、プロセッサにはいくつかのキャッシュレベル（L1、L2、L3）があります。正確なアーキテクチャは、製造元、CPUモデル、およびその他の要因によって異なります。ただし、L3はすべてのコアで共有されますが、ほとんどの場合、L1およびL2キャッシュは各コアでローカルに動作します。

SMPアーキテクチャ

キャッシュがプロセッサコアに近いほど、アクセスレイテンシとキャッシュサイズが小さくなります。

キャッシュ	ディレイ	CPUサイクル	サイズ
L1	〜1.2 ns	〜4	32〜512 KB
L2	〜3 ns	〜10	128 KB〜24 MB
L3	〜12 ns	〜40	2〜32 MB

この場合も、正確な数値はプロセッサモデルによって異なります。おおよその見積もりでは、メインメモリへのアクセスに60 nsかかる場合、L1へのアクセスは約50倍速くなります。

プロセッサの世界では、リンクの局所性という重要な概念があります。プロセッサが特定のメモリ位置にアクセスする場合、以下の可能性があります。

近い将来、同じメモリ位置を参照します-これは時間の局所性の原則です。
彼は近くにあるメモリセルに言及します-これは距離による局所性の原則です。

時間の局所性は、CPUキャッシュの理由の1つです。しかし、距離局所性をどのように使用しますか？解決策-1つのメモリセルをCPUキャッシュにコピーする代わりに、キャッシュラインがそこにコピーされます。キャッシュラインは、メモリの連続したセグメントです。

キャッシュラインサイズは、キャッシュレベル（およびプロセッサモデル）によって異なります。たとえば、私のマシンのL1キャッシュラインのサイズは次のとおりです。

$ sysctl -a | grep cacheline
hw.cachelinesize: 64

1つの変数をL1キャッシュにコピーする代わりに、プロセッサは64バイトの連続したセグメントをそこにコピーします。たとえば、Goスライスの単一のint64要素をコピーする代わりに、その要素と7つのint64要素をコピーします。

Goのキャッシュラインの特定の使用法

プロセッサキャッシュの利点を示す具体的な例を見てみましょう。次のコードでは、int64要素の2つの正方行列を追加します。

func BenchmarkMatrixCombination(b *testing.B) {
    matrixA := createMatrix(matrixLength)
    matrixB := createMatrix(matrixLength)

    for n := 0; n < b.N; n++ {
        for i := 0; i < matrixLength; i++ {
            for j := 0; j < matrixLength; j++ {
                matrixA[i][j] = matrixA[i][j] + matrixB[i][j]
            }
        }
    }
}

matrixLength64kの場合、次の結果が生成されます。

BenchmarkMatrixSimpleCombination-64000                     8  130724158 ns/op

ここで、代わりに、以下matrixB[i][j]を追加しますmatrixB[j][i]。

func BenchmarkMatrixReversedCombination(b *testing.B) {
    matrixA := createMatrix(matrixLength)
    matrixB := createMatrix(matrixLength)

    for n := 0; n < b.N; n++ {
        for i := 0; i < matrixLength; i++ {
            for j := 0; j < matrixLength; j++ {
                matrixA[i][j] = matrixA[i][j] + matrixB[j][i]
            }
        }
    }
}

これは結果に影響しますか？

BenchmarkMatrixCombination-64000                           8  130724158 ns/op
BenchmarkMatrixReversedCombination-64000                   2  573121540 ns/op

はい、ありました。これはどのように説明できますか？

何が起こっているのかを描いてみましょう。青い円は最初のマトリックスを示し、ピンクの円は2番目のマトリックスを示します。を設定するmatrixA[i][j] = matrixA[i][j] + matrixB[j][i]と、青いポインターは位置（4.0）にあり、ピンクのポインターは位置（0.4）にあります。

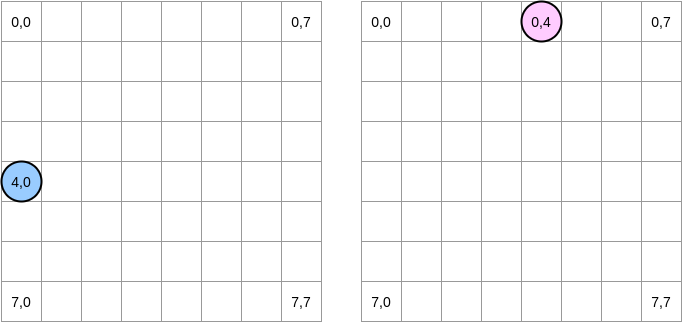
注。この図では、行列は数学的な形式で示されています。横座標と縦座標があり、位置（0,0）は左上の正方形にあります。メモリでは、マトリックスのすべての行が順番に配置されます。ただし、わかりやすくするために、数学的表現を見てみましょう。さらに、次の例では、行列のサイズはキャッシュラインのサイズの倍数です。したがって、キャッシュラインは次の行に「追いつきません」。それは複雑に聞こえますが、例はすべてを明確にします。

マトリックスをどのように反復するのでしょうか？青いポインタは、最後の列に到達するまで右に移動し、次に位置（5,0）で次の行に移動します。逆に、ピンクのポインターは下に移動し、次の列に移動します。

ピンクのポインタが位置（0.4）に到達すると、プロセッサはライン全体をキャッシュします（この例では、キャッシュラインのサイズは4つの要素です）。ピンクのポインターが位置（0.5）に到達すると、変数は既にL1に存在していると想定できますよね？

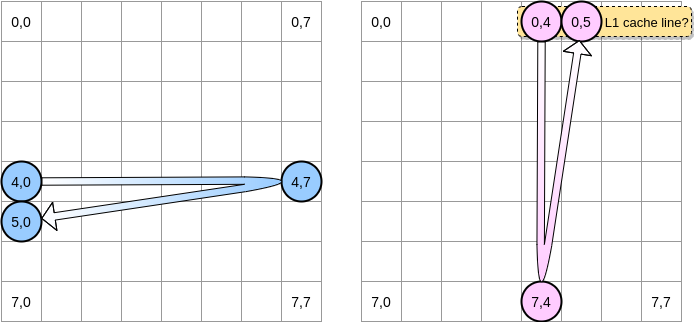
答えは行列のサイズによって異なります。

行列がL1のサイズと比較して十分に小さい場合、はい、要素（0.5）は既にキャッシュされています。
それ以外の場合、ポインターが位置（0.5）に到達する前に、キャッシュラインがL1から削除されます。したがって、キャッシュミスが発生し、プロセッサは、L2などを介して別の方法で変数にアクセスする必要があります。この状態になります。

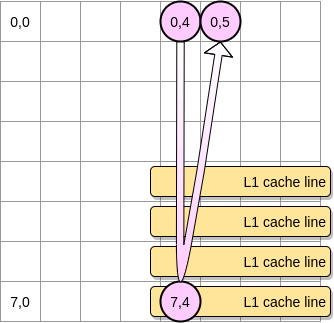
L1の恩恵を受けるには、マトリックスをどの程度小さくする必要がありますか？少し数えてみましょう。まず、L1キャッシュのサイズを知る必要があります。

$ sysctl hw.l1dcachesize
hw.l1icachesize: 32768

私のマシンでは、L1キャッシュラインは64バイトですが、L1キャッシュは32,768バイトです。このようにして、L1に最大512のキャッシュラインを格納できます。512要素の行列で同じベンチマークを実行するとどうなるでしょうか。

BenchmarkMatrixCombination-512            1404   718594 ns/op
BenchmarkMatrixReversedCombination-512    1363   850141 ns/opp

ギャップは修正しましたが（64kマトリックスでは、約4倍の差がありました）、まだわずかな違いに気づくことができます。何が悪いのでしょうか？ベンチマークでは、2つの行列を使用します。したがって、プロセッサは両方のキャッシュラインを保持する必要があります。理想的な世界（他のアプリケーションが実行されていないなど）では、L1キャッシュは50％が最初のマトリックスのデータで、50％が2番目のマトリックスで満たされます。マトリックスのサイズを半分に減らして、256個の要素を処理するとどうなるでしょうか。

BenchmarkMatrixCombination-256             5712   176415 ns/op
BenchmarkMatrixReversedCombination-256     6470   164720 ns/op

最後に、2つの結果が（ほぼ）同等になるポイントに達しました。

. ? , Go. - LEA (Load Effective Address). , . LEA .

, int64 , LEA , 8 . , . , . , () .

さて、行列が大きい場合にキャッシュミスの影響を制限するにはどうすればよいですか？ネストループの最適化（ループネスト最適化）と呼ばれる方法があります。キャッシュラインを最大限に活用するには、特定のブロック内でのみ反復する必要があります。

この例のブロックを4つの要素の正方形として定義しましょう。最初の行列では、（4.0）から（4.3）まで反復します。次に、次の行に移動します。したがって、次の列に進む前に、（0.4）から（3.4）までの2番目の行列のみを反復処理します。

ピンクのポインターが最初の列に移動すると、プロセッサは対応するキャッシュラインを格納します。したがって、残りのブロックを検討することは、L1を利用することを意味します。

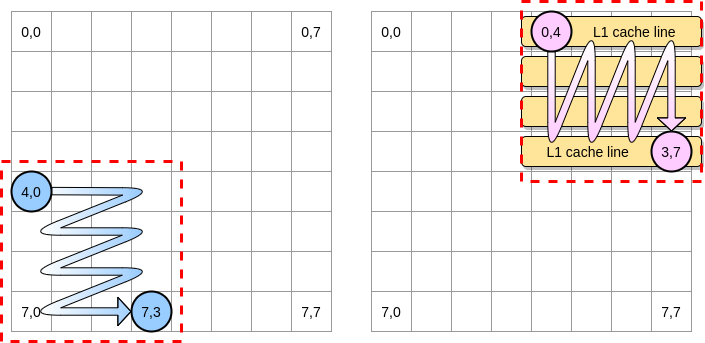
Goでこのアルゴリズムの実装を書いてみましょう。ただし、最初にブロックサイズを慎重に選択する必要があります。前の例では、キャッシュラインと同じでした。小さくしてはいけません。さもなければ、アクセスできない要素を格納します。

Goベンチマークでは、int64要素（各8バイト）を格納します。キャッシュラインは64バイトなので、8アイテムを保持できます。次に、ブロックサイズの値は少なくとも8でなければなりません。

func BenchmarkMatrixReversedCombinationPerBlock(b *testing.B){
    matrixA := createMatrix(matrixLength)
    matrixB := createMatrix(matrixLength)
    blockSize := 8

    for n := 0; n < b.N; n++ {
        for i := 0; i < matrixLength; i += blockSize {
            for j := 0; j < matrixLength; j += blockSize {
                for ii := i; ii < i+blockSize; ii++ {
                    for jj := j; jj < j+blockSize; jj++ {
                        matrixA[ii][jj] = matrixA[ii][jj] + matrixB[jj][ii]
                    }
                }
            }
        }
    }
}

行/列全体を繰り返し処理した場合よりも、実装が67％以上速くなりました。

BenchmarkMatrixReversedCombination-64000          2  573121540 ns/op
BenchmarkMatrixReversedCombinationPerBlock-64000  6  185375690 ns/op

これは、CPUキャッシュの動作を理解することが、より効率的なアルゴリズムの設計に役立つことを示す最初の例でした。

偽りの共有

これで、プロセッサが内部キャッシュを管理する方法がわかりました。簡単な要約として：

距離による局所性の原則により、プロセッサは1つのメモリアドレスだけでなく、キャッシュラインも使用します。
L1キャッシュは1つのプロセッサコアに対してローカルです。

次に、L1キャッシュコヒーレンシの例について説明します。メインメモリには2つの変数var1とが格納されますvar2。1つのコア上の1つのスレッドがアクセスvar1し、他のコア上の別のスレッドがアクセスしvar2ます。両方の変数が連続的（またはほぼ連続的）であるとvar2すると、両方のキャッシュに存在する状況になります。

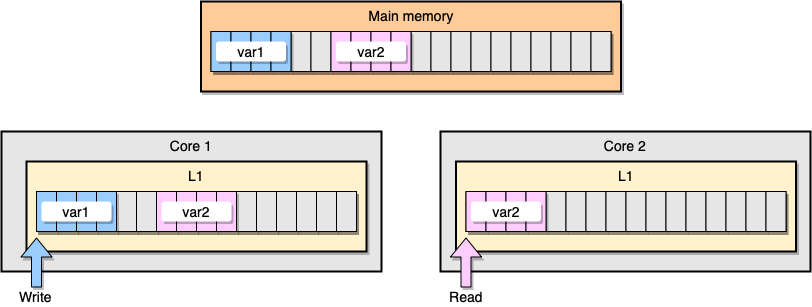
例L1キャッシュ

最初のスレッドがキャッシュラインを更新するとどうなりますか？を含む、文字列の任意の場所を更新する可能性がありますvar2。次に、2番目のスレッドがを読み取るvar2ときに、値が一貫していない可能性があります。

プロセッサはどのようにキャッシュの一貫性を保ちますか？ 2つのキャッシュラインに共有アドレスがある場合、プロセッサはそれらを共有としてマークします。 1つのスレッドが共有回線を変更すると、両方が変更済みとしてマークされます。コア間の調整は、キャッシュの一貫性を確保するために必要であり、アプリケーションのパフォーマンスを大幅に低下させる可能性があります。この問題は、偽共有と呼ばれます。

特定のGoアプリケーションを考えてみましょう。この例では、2つの構造を次々に作成します。したがって、これらの構造はメモリ内でシーケンシャルである必要があります。次に、2つのゴルーチンを作成し、それぞれが独自の構造を参照します（Mは100万に等しい定数です）。

type SimpleStruct struct {
    n int
}

func BenchmarkStructureFalseSharing(b *testing.B) {
    structA := SimpleStruct{}
    structB := SimpleStruct{}
    wg := sync.WaitGroup{}

    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        wg.Add(2)
        go func() {
            for j := 0; j < M; j++ {
                structA.n += j
            }
            wg.Done()
        }()
        go func() {
            for j := 0; j < M; j++ {
                structB.n += j
            }
            wg.Done()
        }()
        wg.Wait()
    }
}

この例では、2番目の構造体の変数nは、2番目のゴルーチンにのみ使用できます。ただし、構造はメモリ内で隣接しているため、変数は両方のキャッシュラインに存在します（両方のゴルーチンが別々のコアのスレッドでスケジュールされていると仮定しますが、これは必ずしもそうではありません）。ベンチマーク結果は次のとおりです。

BenchmarkStructureFalseSharing         514    2641990 ns/op

誤った情報共有を防ぐには？1つの解決策は、完全なメモリ（メモリパディング）です。私たちの目標は、2つの変数の間に十分なスペースを確保して、それらが異なるキャッシュラインに属するようにすることです。

最初に、変数を宣言した後にメモリを埋めて、前の構造の代替を作成します。

type PaddedStruct struct {
    n int
    _ CacheLinePad
}

type CacheLinePad struct {
    _ [CacheLinePadSize]byte
}

const CacheLinePadSize = 64

次に、2つの構造体をインスタンス化し、これらの2つの変数に別々のゴルーチンで引き続きアクセスします。

func BenchmarkStructurePadding(b *testing.B) {
    structA := PaddedStruct{}
    structB := SimpleStruct{}
    wg := sync.WaitGroup{}

    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        wg.Add(2)
        go func() {
            for j := 0; j < M; j++ {
                structA.n += j
            }
            wg.Done()
        }()
        go func() {
            for j := 0; j < M; j++ {
                structB.n += j
            }
            wg.Done()
        }()
        wg.Wait()
    }
}

メモリの観点からは、この例は2つの変数が異なるキャッシュラインの一部であるように見えるはずです。

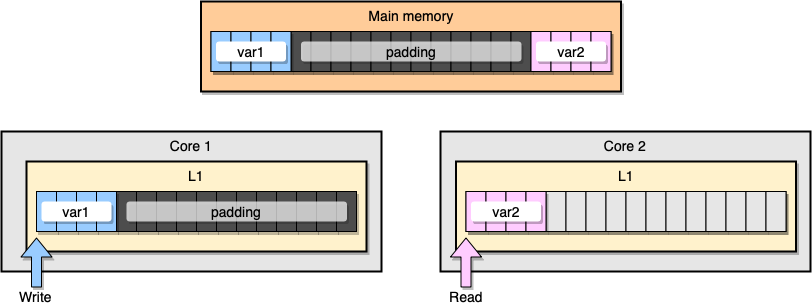
メモリ充填

結果を見てみましょう：

BenchmarkStructureFalseSharing         514    2641990 ns/op
BenchmarkStructurePadding              735    1622886 ns/op

メモリを埋める2番目の例は、元の実装よりも約40％高速です。しかし、マイナス面もあります。このメソッドはコードを高速化しますが、より多くのメモリを必要とします。

アプリを最適化することに関しては、メカニックが重要です。この記事では、CPUの理解がプログラム速度の向上にどのように役立つかについての例を見てきました。

他に読むべきもの：

GoとCPUキャッシュ

基礎

Goのキャッシュラインの特定の使用法

偽りの共有

More articles: