👸🏿 👨🏽‍🏫 ✍🏽 Pythonを使用したベイジアンネットワーク-何を、なぜ？ 😅 👴🏽 👚

免責事項：この記事は改作された翻訳です。原本はこちらから読むことができます。

Pythonを使用したベイジアンネットワーク-例で説明

情報が限られていること（特にネイティブロシア語）と作業のリソースにより、ベイジアンネットワークは多くの問題に囲まれています。また、人工知能や機械学習など、当時の高度なテクノロジーのほとんどに実装されていなければ、十分に眠ることができます。

この事実に基づいて、この記事は完全にベイジアンネットワークの仕事とそれら自体が問題を形成できない方法に専念していますが、解決される問題が非常に混乱している場合でも、それらを解決するために適用されます。

記事の構造

ベイジアンネットワークとは
有向非循環グラフとは何ですか？
ベイジアンネットワークにはどんな数学がありますか
ベイジアンネットワークの考え方を反映した例
ベイジアンネットワークの本質
Pythonのベイジアンネットワーク
ベイジアンネットワークの応用

行こう。

ベイジアンネットワークとは

ベイジアンネットワークは、確率的グラフィカルモデル（GPM）のカテゴリに分類されます。VGMは、確率の概念におけるアプリケーションの変動性を計算するために使用されます。

ベイジアンネットワークの一般的な名前はディープネットワークです。それらは有向非循環グラフのモデル化に使用されます。

有向非循環グラフとは何ですか？

有向非循環グラフ（統計のグラフと同様）はノードとリンクの構造であり、ノードはいくつかの値を担当し、リンクはノード間の関係を反映します。

非循環==有向周期がない。グラフの文脈では、この形容詞は、あるポイントからパスを開始すると、グラフのダイアグラム全体ではなく、その一部のみを通過することを意味します。（たとえば、図のノード2から開始すると、ノード1には確実に到達しません）。

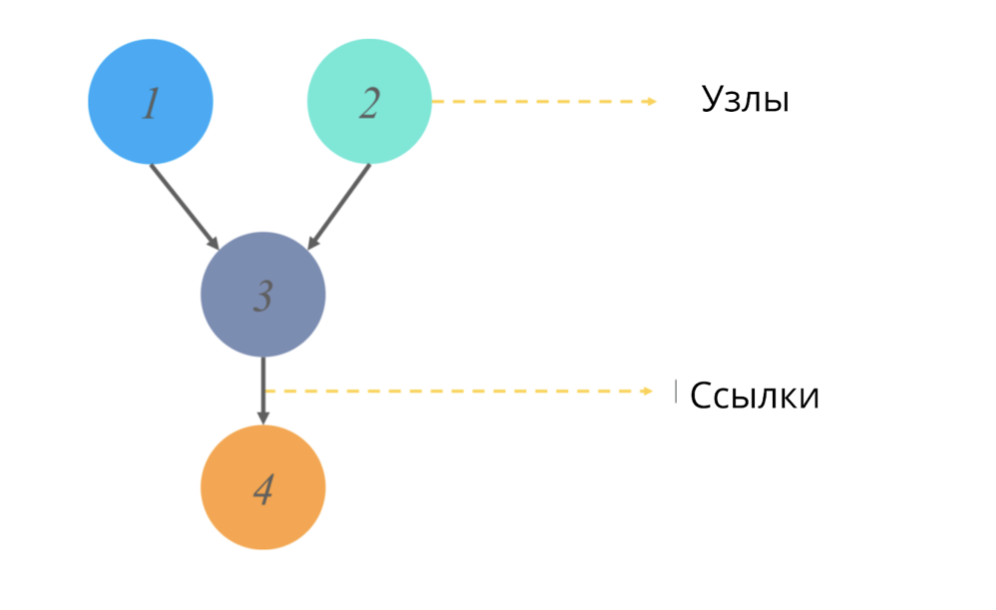
これらのグラフは何をシミュレートし、どのような出力値を提供しますか？

不確かな有向グラフのモデルは、各ランダム値のイベントの確率論的起源の変化にも基づいています。条件付き確率表は、各値を表現および解釈するために適用できるため、連続したイベントの確率の分岐をシミュレートできます。

大丈夫。私も最初は混乱しました。よりよく理解するために、ベイジアンネットワークの数学的な要素を分析しましょう。

ベイジアンネットワーク数学

定義ですでに述べたように、ベイジアンネットワークは確率論に基づいているため、ベイジアンネットワークでの作業を開始する前に、2つの質問に対処する必要があります

。条件付き確率とは何ですか？

同時平均確率分布とは何ですか？

条件付き確率

一部のXイベントの条件付き確率は、何らかのイベントYがすでに発生している場合に、イベントXが発生する確率の数値です。

1つの値の標準確率式（記事には記載されていません）：P（X）= n（x）/N。nは調査中のイベントで、Nはすべて可能なイベントです。

2つの値の場合、次の式が適用されます

。XとYが依存イベントの場合：

確率Y.ためのP（X又はY）= P（X⋂Y）/ P（Y）、Xの確率との交点及びY /（記号「」分子に確率の交差点を意味する）

イベントX及びYは独立している場合：

P（XまたはY）= P（X）、つまり、調査中のイベントの発生は互いに同等に起こりそうです。

結合確率

結合確率は、同時に発生する2つ以上のイベントの統計的尺度の定義です。つまり、イベントX、Y、およびCが一緒に発生し、値P（X⋂Y⋂C）を使用してそれらの累積確率を反映するとします。

これはベイジアンネットワークでどのように機能しますか？例を見てみましょう。

ベイジアンネットワークの本質を反映する例

試験で学生の成績の1つを取得する確率をモデル化する必要があるとしましょう。

スコアは以下で構成されます。

試験の難易度（e）：2段階の離散変数（難しい、簡単）
Student IQ：2つのグラデーション（低、高）を持つ離散変数

結果として得られる評価値は、学生または女子学生が大学に入る確率の予測子（予測値）として使用されます。

ただし、IQ変数も入学に影響を与えます。

有向非循環グラフと条件付き確率分布表を使用してすべての値を表現します。

この表現を使用して、5つの変数の条件付き確率の積から形成されるいくつかの累積確率を計算できます。

累積確率：

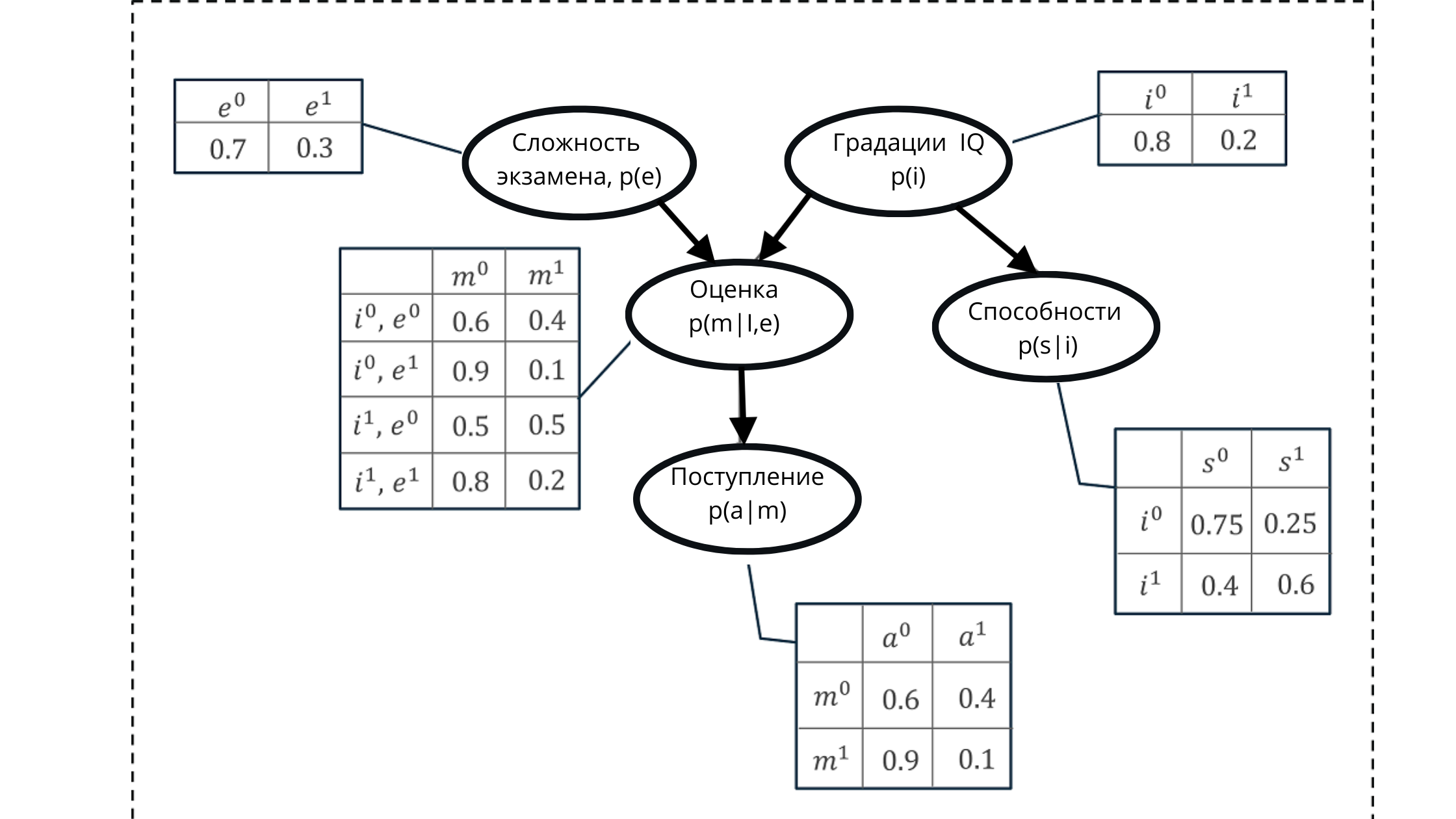
p (a, m, i, e, s) = p (i) * p (e) * p (s | i) * p (a | m) * p (m | i, e) p (a, m, i, e, s) = p (i) * p (e) * p (s | i) * p (a | m) * p (m | i, e)

$p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)$

図で

は、p（e）は試験変数のグレードの確率分布です（グレードp（m | i、e）に影響します））

p（i）はIQ変数のグレードの確率分布です（グレードp（m | i、eに影響します））））

p（m | i、e）-IQレベルと試験の難易度に基づく、成績評価の確率分布（p（i）とp（e）に依存）

p（s | i）-学生の能力の確率係数、IQのレベルに基づいて（変数IQ p（i）に依存）

p（a | m）は、彼の推定値p（m | i、e）に基づく学生の大学入学の確率です。

ここで、非循環グラフの特性は反射であることを思い出します関係。この図では、親ノードが子にどのように影響するか、および子が親にどのように依存するかを明確に見ることができます。

したがって、ベイジアンネットワークを使用して生成された値のセットの定式化が出現します。

ベイジアンネットワークの本質

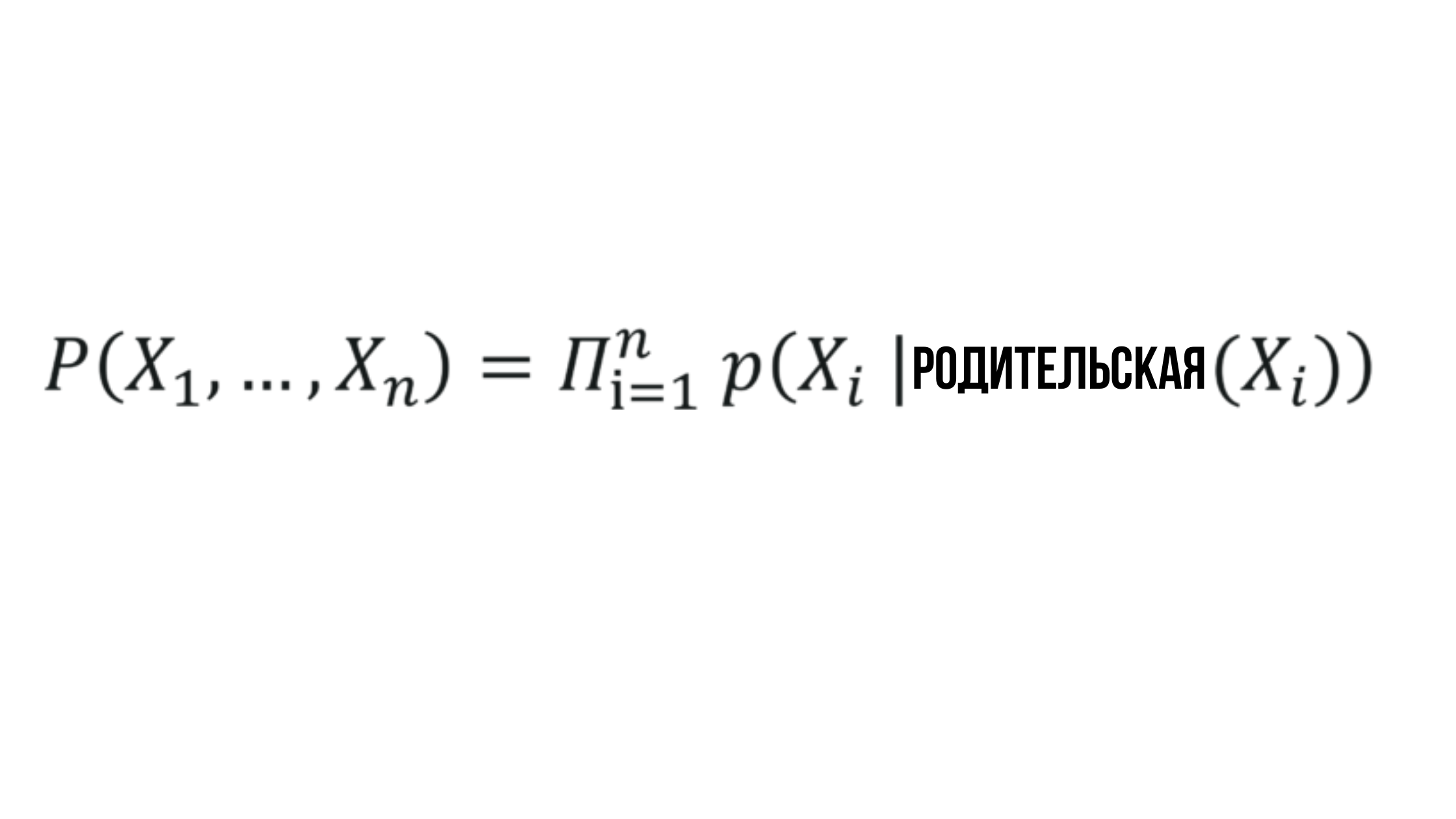
確率X_iは、対応する親ノードの確率に依存し、任意のランダムな値で表すことができます。

簡単に聞こえますが、その通りです。ベイジアンネットワークは、記述分析や予測モデリングなどで使用される最も単純な方法の1つです。

Pythonのベイジアンネットワーク

モンティホールパラドックスと呼ばれる問題にベイジアンネットワークを適用する方法を見てみましょう。

結論：あなたが「Field of Miracles」ゲームのアップデート形式の参加者であると想像してください。ドラムは回転しなくなりました。今度はFを適用するのではなく、pを使用してください。

目の前には3つのドアがあり、その後ろに1台の車が配置されている可能性が高いです。後ろに車がないドアが山羊へとあなたを導きます。

選択した後、残りのリーダーは山羊に通じる方を開き（たとえば、ドア1を選択した、つまりリーダーがドア2または3のいずれかを開くことを意味します）、選択を変更するように勧めます。

質問：何をすべきか？

解決策：最初は車でドアを選択する確率= 33％、山羊でドア= 66％。

33％に当たった場合、ドアを変更すると、損失につながります=>勝つ可能性== 33％
66％ヒットすると、変化は勝利につながります=>勝利の確率== 66％

数学的論理の観点から見ると、ドアを全体的に変更すると、勝率は66％になり、損失は33％になります。したがって、正しい戦略はドアを変更することです。

ただし、ここではネットワークについて話しているため、多数のドアが存在する可能性があるため、ソリューションをモデルに転送します。

3つのノードを持つ有向非循環グラフを作成してみましょう。

プライズドア（常に車で）
選択可能なドア（車または山羊付き）
イベント1の開閉可能なドア（常に山羊がいる）

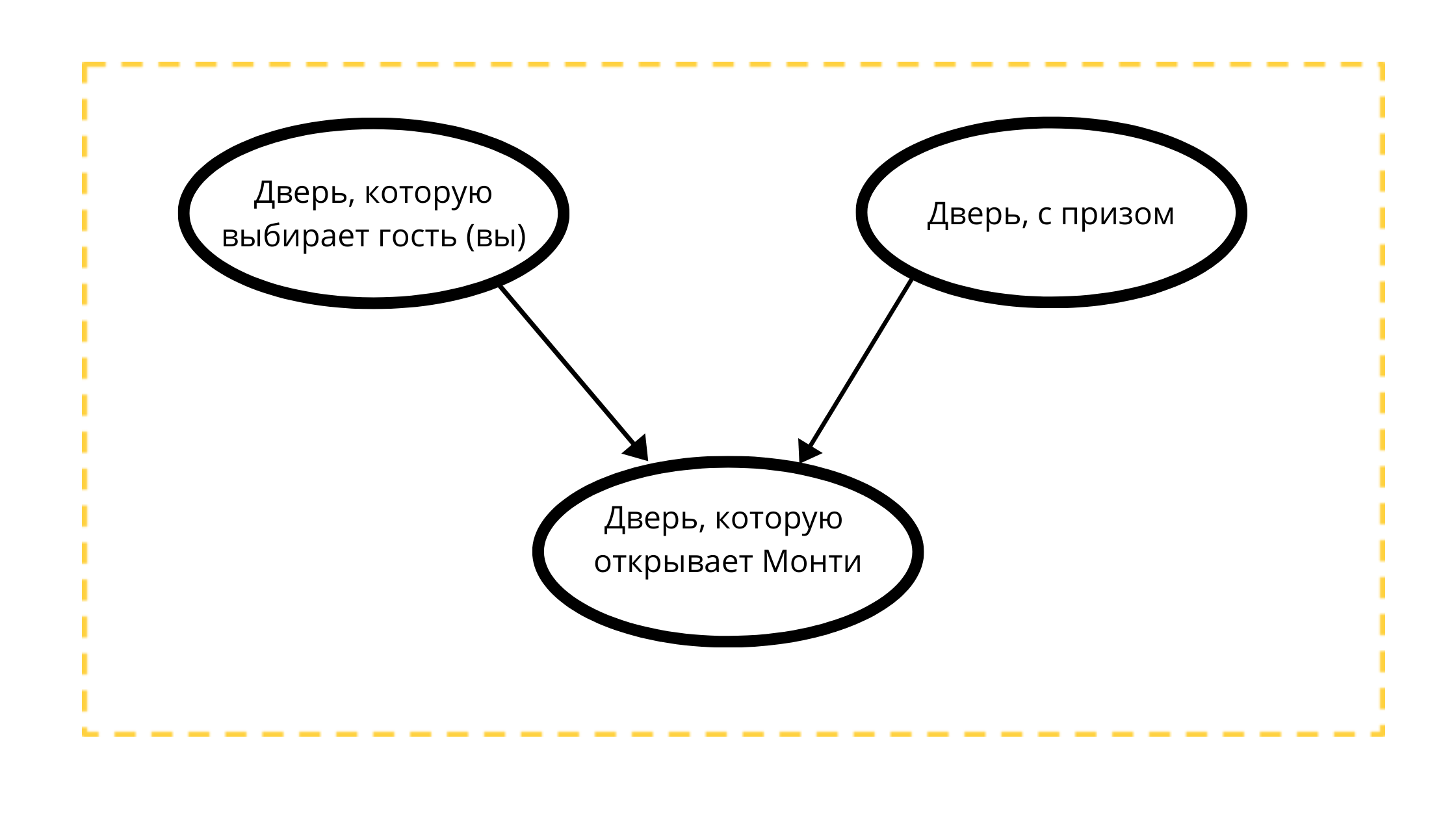
カウントの読み取り：

モンティが開くドアは、2つの変数によって厳密に影響を受けます。

ゲスト（あなた）が選んだドアtk Monti 100％はあなたの選択を開きません
賞品のあるドア、おそらくモンティは常に賞品以外のドアを開きます。

古典的な例の数学的条件によれば、賞品はドアを選択するのと同じように、ドアの後ろに位置する可能性があります。

#   
import math
from pomegranate import *
 
#    "  " (   3)
guest =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
#    "   " (    )
prize =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
#  ,       ,     
#    
monty =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
 
d1 = State( guest, name="guest" )
d2 = State( prize, name="prize" )
d3 = State( monty, name="monty" )
 
#  
network = BayesianNetwork( "Solving the Monty Hall Problem With Bayesian Networks" )
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()

スニペットでは、値は次のとおりです。

A-ゲストが選択したドア
B-賞品のドア
C-モンティが選んだドア

フラグメントでは、グラフの各ノードの確率値を計算します。この例では、上位2つのノードは等確率分布に従い、3番目のノードは従属分布を反映しています。したがって、価値を失わないために、ゲームの可能な組み合わせのそれぞれの確率がに対して計算されます。

データを準備したら、ベイジアンネットワークを作成します。

このようなネットワークの特性の1つは、オブザーバブルに対する隠し変数の影響を明らかにすることです。同時に、非表示の変数も監視可能な変数も事前に指定または決定する必要はありません。モデル自体が非表示の変数の影響を調べ、受け取る変数が多いほど、これをより正確に行います。

予測を始めましょう。

beliefs = network.predict_proba({ 'guest' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
 
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}

変数Aの例を使用してフラグメントを分析してみましょう。

ゲストがそれを選択したとします（A）。

ゲストがドアを選択する段階での「ドアの後ろに賞品がある」というイベントは、確率分布== hasです（各ドアは同じ確率で賞品になる可能性があるため）。

次に、ドアがモンティによって選択された段階で、ドアが賞である確率の値を追加します。ステップ1では、プライズドアが私たち自身（ゲスト）の選択によって除外されたかどうかはわからないため、この段階でドアがプライズである確率は50/50です。

beliefs = network.predict_proba({'guest' : 'A', 'monty' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B

このステップでは、ネットワークの入力値を変更します。これで、ステップ1と2で得られた確率分布が機能します。

私たちが選んだドアで勝つチャンスは変わっていません（33％）
モンティ（B）によって開かれたドアで賞を獲得するチャンスはキャンセルされました
無人で放置されたドアでの賞品になる可能性は66％の値を取りました

したがって、上記で結論されたように、このゲームのゲスト側の正しい戦略はドアを変更することです。ドアを変更する人は数学的にドアを変更しない人に勝つ可能性があります（⅔）。

3つのノードがある例では、間違いなく手動の計算で十分ですが、変数、ノード、および影響因子の数が増えると、ベイジアンネットワークは予測値の問題を解決できます。

ベイジアンネットワークの応用

1.診断：

症状に基づく疾患の予測
基礎疾患の症状モデリング

2.インターネットの検索：

ユーザーコンテキスト（意図）の分析に基づく検索結果の形成

3.文書の分類：

コンテキスト分析に基づくスパムフィルター
カテゴリ/クラスごとのドキュメントの配布

4.遺伝子工学

DNAセグメントの相互接続と関係に基づく遺伝子調節ネットワークの挙動のモデリング

5.医薬品：

許容線量のモニタリングと予測値

上記の例は事実です。完全に理解するには、ベイジアンネットワークの作成がどの段階で接続され、それを表すグラフがどのノードで構成されるかを想像することが適切です。

モンティホールパラドックスの問題は、依存する確率分布と独立した確率分布の組み合わせに基づくチェーンの動作を「指先」で説明できるようにするための基盤にすぎません。よかったです。

PS私はPythonのエースではなく、単に学んでいるだけなので、著者のコードについて責任を負うことはできません。この記事のハブレに関する出版は、翻訳の知的作品の世界へのさらなるリリースを追求しています。将来的には、私自身のチュートリアルを生成できるようになると思います。それらのチュートリアルでは、コードについての建設的な考えを見て喜んでいます。

Pythonを使用したベイジアンネットワーク-何を、なぜ？