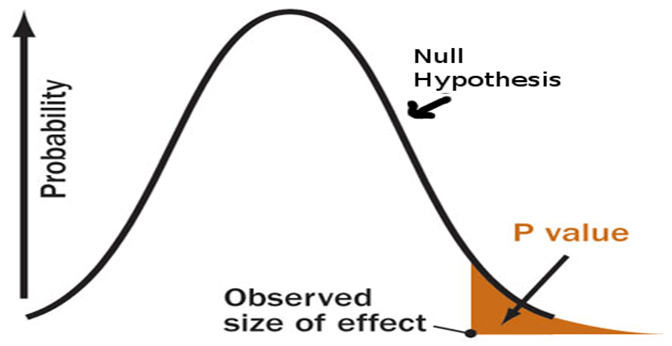
当時、私はp値、仮説テスト、さらには統計的有意性についても何も知りませんでした。
私は「p-value」という単語をグーグルで検索することにしました。ウィキペディアで見つけたものは私をさらに混乱させました...
統計的仮説をテストする場合、特定の統計モデルのp値または確率値は、null仮説が真である場合、統計的要約(たとえば、2つの比較されたグループ間の差のサンプル平均の絶対値)が実際に観測された結果以上になる確率です。よくやった、ウィキペディア。
-ウィキペディア
はい。 p値が実際に何を意味するのか理解できませんでした。
データサイエンスの分野を深く掘り下げていくうちに、ついにp値の意味と、特定の実験で意思決定ツールの一部として使用できる場所を理解し始めました。
そこで、この記事でp値を説明し、仮説テストでどのように使用できるかを説明して、p値をよりよく直感的に理解できるようにすることにしました。
また、他の概念の基本的な理解とp値の定義を見逃すことはできません。私が遭遇したすべての専門用語に触れることなく、この説明を直感的にすることを約束します。
この記事には、仮説テストの作成からp値の理解、および意思決定プロセスでの使用までの全体像を示すために、合計4つのセクションがあります。p値を詳細に理解するために、これらすべてを確認することを強くお勧めします。
- 仮説テスト
- 正規分布
- P値とは何ですか?
- 統計的有意性
楽しいですよ。
はじめましょう!
1.仮説のテスト
p値の意味について説明する前に、仮説テストを見てみましょう。ここでは、p値を使用して結果の統計的有意性を判断します。
私たちの最終的な目標は、結果の統計的有意性を判断することです。
そして、統計的有意性は、次の3つの単純なアイデアに基づいています。
- 仮説テスト
- 正規分布
- P値
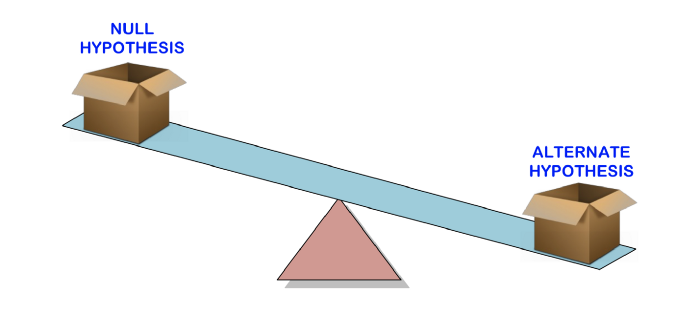
仮説テストは、サンプルデータを使用して母集団について作成されたステートメント(null仮説)の有効性をテストするために使用されます。別の仮説は、ヌル仮説が間違っていることが判明した場合に信じられる仮説です。
つまり、クレーム(null仮説)を作成し、サンプルデータを使用してクレームが有効かどうかを確認します。ステートメントが正しくない場合は、別の仮説を選択します。すべてがとてもシンプルです。
主張が有効かどうかを確認するために、p値を使用して証拠の強度を比較検討し、統計的に有意であるかどうかを確認します。証拠が代替仮説を支持する場合、ヌル仮説を拒否し、代替仮説を受け入れます。これについては、次のセクションで説明します。
この概念を明確にするために例を使用してみましょう。この例は、この記事全体で他の概念に使用されます。
例。ピッツェリアの配達時間は平均30分以下であると主張しているが、記載されているよりも長いと考えているとします。したがって、仮説テストを実行し、納期をランダムに選択してクレームをテストします。
- — 30
- — 30
- , , — — , .
この場合、平均配信時間が30分を超えることが重要であるため、一方向テストを使用します。平均納期が30分以下の結果がさらに望ましいため、この可能性を他の方向では考慮しません。ここでは、平均納期が30分を超える可能性があるかどうかを確認します。言い換えれば、ピッツェリアが私たちをだましていないかどうかを確認したいのです。
仮説をテストする一般的な方法の1つは、Zテストを使用することです。深く掘り下げる前に、表面で何が起こっているのかをよりよく理解したいので、ここでは詳細には立ち入りません。
2.正規分布
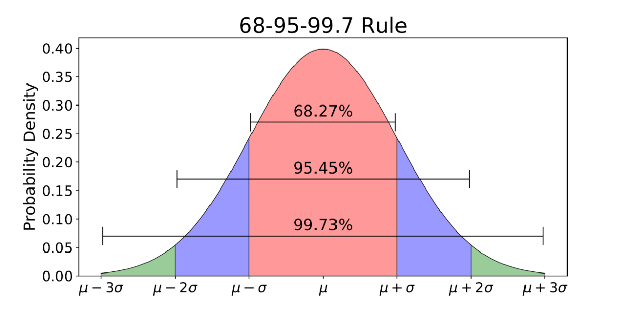
正規分布は、データの分布を表示するために使用される確率密度関数です。
正規分布には、平均(μ)とシグマ(σ)とも呼ばれる標準偏差の2つのパラメーターがあります。
平均は、分布の中心的な傾向です。これは、正規分布のピークの位置を定義します。標準偏差は変動性の尺度です。それは、値が平均からどれだけ離れる傾向があるかを決定します。
通常の分布は通常、68-95-99.7ルールに関連付けられています(上の画像)。
- データの68%は、平均(μ)の1標準偏差(σ)以内です。
- データの95%は、平均(μ)の2標準偏差(σ)以内です。
- データの99.7%は、平均(μ)の3標準偏差(σ)以内です。
最初に話したヒッグスボソンの5シグマのしきい値を 覚えていますか?5シグマは、科学者がヒッグスボソンの発見を確認する前に受信する必要があるデータの約99.99999426696856%です。これは、誤った信号の可能性を回避するために設定された厳密なしきい値でした。
涼しい。ここで、「正規分布は以前の仮説テストとどのように関連しているのか」と疑問に思われるかもしれません。
Zテストを使用して仮説をテストしたため、Zスコアを計算する必要があります(これはテスト統計で使用されます))、これはデータポイントの平均からの標準偏差の数です。私たちの場合、各データポイントは私たちが受け取ったピザの配達時間です。 以下に示すように、ピザの配達時間ごとにすべてのZスコアを計算し、標準の正規分布曲線をプロットすると、平均を差し引いて除算することで変数を標準化すると、X軸の単位が分から標準偏差の単位に変化することに注意してください。その標準偏差による(上記の式を参照)。 「通常の」母集団からのテスト結果を標準偏差の標準化された単位と比較できるため、特に異なる単位が付属する変数がある場合は、標準のベル曲線を調べると便利です。

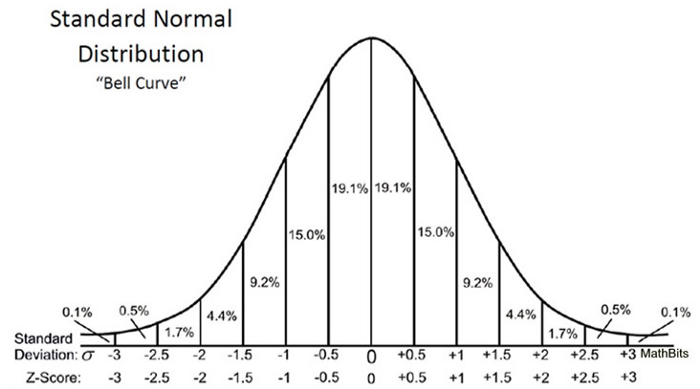
zスコアは、平均的な人口と比較して、全体的なデータがどこにあるかを教えてくれます。
私はウィル・カーセンの言い方が好きです。Zスコアが高いか低いほど、ランダムな結果が発生する可能性は低くなり、意味のある結果が得られる可能性が高くなります。
しかし、私たちの結果がどれほど重要であるかを定量化するのに十分に説得力があると考えられるのはどれくらい高い(または低い)のでしょうか?
クライマックス
ここでは、パズルを解くための最後のピースであるp値が必要であり、実験を開始する前に設定した有意水準(アルファとも呼ばれます)に基づいて、結果が統計的に有意であるかどうかを確認します。
3. P値とは何ですか?
最後に...ここでp値について話します!
これまでの説明はすべて、ステージを設定し、このP値に導くことを目的としています。この神秘的な(実際にはそれほど神秘的ではない)p値と、それが仮説をテストする決定にどのようにつながるかを理解するには、前のコンテキストと手順が必要です。
ここまで来たら、読み続けてください。このセクションはそれらすべての中で最もエキサイティングな部分だからです!ウィキペディアの
定義(申し訳ありませんがウィキペディア)を使用してp値を説明する代わりに、私たちのコンテキストで説明しましょう-ピザの配達時間!
念のため、ピザの配達時間をランダムに選択しました。目標は、配達時間が30分を超えているかどうかを確認することです。最終的な証拠がピッツェリアの主張を裏付けている場合(平均配達時間は30分以下)、ヌル仮説を拒否しません。そうでなければ、私たちはヌル仮説に反論します。
したがって、p値の仕事はこの質問に答えることです:
ピザの配達時間が30分以下の世界に住んでいる場合(ヌル仮説は正しい)、実際の生活での私の証拠はどれほど予想外ですか?P値は、この質問に数値(確率)で答えます。
pの値が低いほど、証拠が予想外であるほど、ヌル仮説はばかげているように見えます。
そして、私たちのヌル仮説についてばかげていると感じたとき、私たちは何をしますか?私たちはそれを拒否し、代替の仮説を選択します。
p値が特定の有意水準を下回っている場合(人々はそれをアルファと呼び、私はこれを不条理のしきい値と呼びます-理由を聞かないでください、私には理解しやすいだけです)、ヌル仮説を拒否します。
これで、p値の意味がわかりました。私たちの場合、これを適用しましょう。
ピザの配達時間を計算する際のP値
配信時間に関するサンプルデータをいくつか収集したので、計算を実行したところ、平均配信時間は10分長く、p値は0.03であることがわかりました。
これは、ピザの配達時間が30分以下(ヌル仮説が正しい)の世界では、ランダムなノイズのために平均配達時間が少なくとも10分長くなる可能性が3%あることを意味します。 ..。
p値が小さいほど、ノイズが原因である可能性が低いため、結果はより意味のあるものになります。
私たちの場合、ほとんどの人はp値を誤解しています。
0.03のp値は、結果が偶然によるものである可能性が3%(確率のパーセンテージ)であることを意味しますが、これは正しくありません。人々はしばしば明確な答え(私自身を含む)を望んでいます。それが私が長い間p値の解釈と混同されてきた理由です。
p値は何も証明しません。これは、驚きをインテリジェントな決定の基礎として使用する方法にすぎません。0.03のp値を使用して賢明な決定を下す方法は次のとおりです(重要)。
-キャシーコジルコフ
- 私たちがピッツェリア(私たちの当初の信念)を信じているため、平均配達時間が常に30分以下の世界に住んでいると想像してみてください!
- 収集したサンプルの納期を分析したところ、p値は有意水準0.05より0.03低く(実験前にこの値を設定したと仮定)、統計的に有意であると言えます。
- , 30 , , , , .
- ? ( ) . , , , , , , .
- , — .
今までに、あなたは何かを理解しているかもしれません...私たちの文脈によっては、p値は何かを証明または正当化するために使用されていません。
私の意見では、結果が統計的に有意である場合、p値は私たちの最初の信念(ヌル仮説)に挑戦するためのツールとして使用されます。私たちが自分の信念でばかげていると感じた瞬間(p値が結果が統計的に有意であることを示していると仮定)、私たちは元の信念を破棄し(ヌル仮説を拒否し)、インテリジェントな決定を下します。
4.統計的有意性
最後に、これはすべてをまとめて、結果が統計的に有意であるかどうかを確認する最後の段階です。
p値だけで十分ではなく、しきい値(有意水準-アルファ)を設定する必要があります。バイアスを避けるために、実験する前に常にアルファを設定する必要があります。観測されたp値がアルファよりも低い場合、結果は統計的に有意であると結論付けます。
基本的なルールは、アルファを0.05または0.01に設定することです(ここでも、値はタスクによって異なります)。
前述のように、実験を開始する前にアルファを0.05に設定したとすると、0.03のp値はアルファよりも低いため、結果は統計的に有意です。
参考までに、実験全体の主な手順は次のとおりです。
- ヌル仮説を立てる
- 代替仮説を立てる
- 使用するアルファ値を決定します
- アルファレベルに関連付けられているZスコアを見つけます
- この式を使用してテスト統計を検索します
- テスト統計がアルファZスコアよりも小さい場合(またはp値がアルファ値よりも小さい場合)、ヌル仮説を拒否します。それ以外の場合は、null仮説を拒否しないでください。
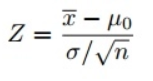
統計的有意性について詳しく知りたい場合は、WillKersenによって書かれたこの記事-統計的有意性の説明をお気軽にチェックしてください。
その後の反省
ここには消化することがたくさんありますね。
私はp値が本質的に多くの人々を混乱させていることを否定することはできません、そしてp値とそれらが私たちの意思決定プロセス内でどのように適用されるかを本当に理解して理解するのにかなりの時間がかかりました。データ科学者として。
ただし、p値は意思決定プロセス全体のごく一部にしか役立たないため、p値にあまり依存しないでください。
私のp値の説明が直感的で、p値が実際に何を意味するのか、そしてそれらを使用して仮説をテストする方法を理解するのに役立つことを願っています。
p値の計算はそれ自体が簡単です。難しい部分は、仮説テストでp値を解釈したいときに発生します。うまくいけば、難しい部分が少し簡単になります。
統計についてもっと知りたい場合は、この本(私が現在読んでいるものです!)を読むことを強くお勧めします-データ科学者が統計の基本概念を理解するために特別に書かれた、データ科学者のための実用的な統計。

SkillFactoryの有料オンラインコースを受講して、注目を集める職業をゼロから取得する方法、またはスキルと給与をレベルアップする方法の詳細をご覧ください。
- データサイエンスの専門家をゼロからトレーニングする(12か月)
- 任意の開始レベルのアナリストの職業(9か月)
- Machine Learning (12 )
- «Python -» (9 )
- DevOps (12 )
- - (8 )