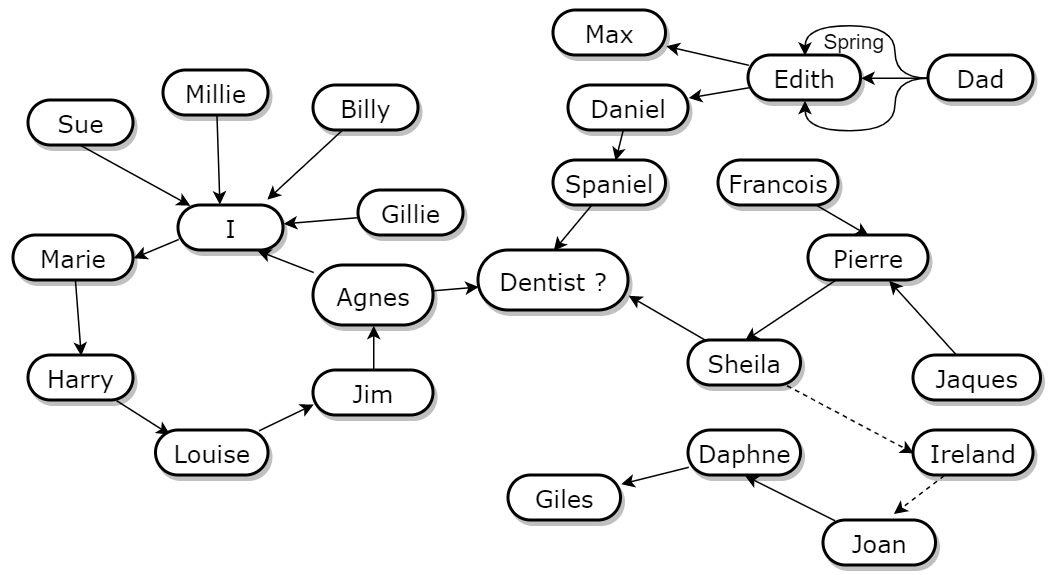
こんにちは同僚！私はHabrについて100年間書いていませんが、今がその時です。この春、私はで高度なMLのコースを教えMADEビッグデータアカデミーMail.ruグループから。リスナーはそれを気に入ったようで、今では私のコースのトピックの1つについての教育的な投稿として広告の投稿を書くように頼まれました。選択は明白に近いものでした。複雑な確率モデルの例として、集団内の疾患の広がりをモデル化する非常に関連性の高い（一見...しかしそれについては後で詳しく説明します）疫学的SIRモデルについて説明しました。マルコフモンテカルロ法による近似推論、ビテルビ確率的アルゴリズムによる隠されたマルコフモデル、さらにはプレゼンスのみのデータなど、すべてが含まれています。



このトピックでは、小さな問題が1つだけ出てきました。講義で実際に話し、示したことについて書き始めました...そして、どういうわけか、20ページのテキスト（写真とコードを含む）が蓄積されましたが、まだまだありません。終了し、自己完結型ではありませんでした。そして、「スクラッチ」から（もちろん絶対的なゼロからではなく）明確になるようにすべてを伝えると、100ページを書くことができます。だからいつか間違いなく書きますが、今のところ、SIRモデルの説明の最初の部分を紹介します。ここでは、問題を提起し、モデルを生成側から説明することしかできません。尊敬される一般の人々が関心を持っている場合は、それが可能になります。続行します。

SIRモデル：問題の説明

私は私の友達を愛し、彼らは私を愛して

います。私たちはできる限り近くにいます。

そして、私たちが本当に気にかけているという理由だけで、私

たちが得るものは何でも、私たちは共有します！



トム・レーラー。アグネスからもらった

それで、それを理解しましょう。非公式には、SIRモデルの基本的な仮定は次のとおりです。

• いくつかのひどいウイルスが歩くことができる人々の特定の人口があります。
• 最初に、ウイルスは何らかの方法で集団に侵入し（たとえば、最初の病気の人が現れます）、次に人々は互いに感染します。
• SIR , :
  
     ○ Susceptible ( , , .. ),
  
     ○ Infected ( )
  
     ○ Recovered ().

簡単にするために、病気の人は常に免疫を発達させ、自然界のウイルスのサイクルから除外されると仮定します。したがって、これらの状態間の遷移は、左から右にのみ行うことができます：感受性→感染→回復。



実際のところ、タスクはこのモデルをトレーニングすることです。つまり、データから感染プロセスのパラメーターについて何かを理解することです。データがどのように見えるかを理解するのは簡単です-それは単に各瞬間に登録された感染者の数であり、ベクトルで示します$$$\boldsymbol{y}$..。たとえば、コロナウイルスのコースで宿題をしたとき（ただし、他のモデルについてでした）、ロシアのデータは次のようになりました。

[2,2,2,2,3,4,6,8,10,10,10,10,15,20,25,30,45,59,63,93,114,147,199,253,306,438,438,495,658,840,1036,1264,1534,1836,2337,2777,3548,4149,4731,5389,6343,7497,8672]

しかし、このモデルのパラメーターが何であるか、それらが互いにどのようにインターフェースするか、そして特にそのような小さなデータセットでそれらをどのようにトレーニングするかは、より深刻な問題です。



一般に、MCMCアルゴリズムがSIR、SEIR、およびそれらのいくつかのバリアント用に構築されている作業の一般的な概要（Fintzi et al。、2016）に従います。しかし、（Fintzi et al。、2016）と比較して、モデルとその表示の両方を大幅に簡略化します。主な単純化は、元の作業で考慮されている連続時間の代わりに、離散時間を考慮することです。つまり、ある時点で「感染」および「回復」タイプのイベントを生成する連続プロセスの代わりに、考慮します。人々が一連の個別の時点を通過すること$$$t=1,\ldots,T$..。この単純化により、まず、多くの技術的な問題を取り除くことができ、次に、一般的なメトロポリス-ヘイスティングスアルゴリズムからギブスサンプリングアルゴリズムに移行できます。つまり、必要に応じてメトロポリス比を計算しません（Fintzi et al。、2016）。私が今言ったことを理解していなくても心配しないでください。今日はこれは必要ありません。次の部分があれば、そこですべてを説明します。



SIRモデルの状態をそれぞれS、I、Rで表し、人の状態を示します。$$$i$ 現時点では $$$t$ -全体 $$$x_i^{(t)}\in\{S, I, R\}$..。同時に、まだ発生していないケースの総数の変数をすぐに導入します$$$S^{(t)}$病気 $$$I^{(t)}$ 回復しました $$$R^{(t)}$ 現時点では $$$t$..。私たちが持っているトータルマン$$$N$だから誰にとっても $$$t$ 実行されます $$$S^{(t)} + I^{(t)} + R^{(t)} = N$..。そして、私が上で書いたように、$$$y^{(t)}$それらのうち、登録された（テストされた）病気の人です。



モデルの未知のパラメータは$$$\boldsymbol\theta = \{\beta, \mu, \rho, \boldsymbol{\pi}\}$どこ：

• $$$\boldsymbol\pi$ -ケースの初期分布。言い換えると、$$$x^{(1)}_j\sim \boldsymbol{\pi}$ それぞれのために $$$j$; 簡略化されたモデルでは、トレーニングは行いません$$$\boldsymbol\pi$、ただし、最初の瞬間に1〜2件のケースを記録するだけです。
• $$$\rho$ -一般の人々の中で感染した人を見つける確率、つまり人が $$$x_j$ 一瞬のうち $$$t$いつ $$$x_j^{(t)}=I$、テストによって検出され、データに登録されます $$$y^{(t)}$; 言い換えれば、病気の人ごとに、テストでそれが見つかるかどうかを判断するためにコインを裏返すので、現在のアイテムは$$$y_t$ パラメータ付きの二項分布を持っています $$$I^{(t)}$ そして $$$\rho$：

  $$

  $$y^{(t)}\mid I^{(t)}, \rho \sim \mathrm{Binomial}(I^{(t)}, \rho);$$

• $$$\mu$ -病気の人が1つのタイムステップで回復する確率、つまり、状態からの移行の確率 $$$I$ 状態で $$$R$;

そして $$$\beta$ -これは、1人の感染者から1回のカウントで感染する可能性を示す最も興味深いパラメータです。これは、モデルでは、人口のすべての人々が互いに「通信」すると仮定していることを意味します（ここでの「通信」は、病気の伝染に十分な接触を意味します。コロナウイルスは主に空中の液滴によって伝染しますが、もちろん、モデル化することは可能です。他の病気の蔓延（たとえば、エピグラフを参照）、および感染する可能性は、現在感染している数、つまり何であるかによって異なります。$$$I^{(t)}$..。1人の感染者からの感染の確率がである最も単純なモデルを想定します$$$\beta$、およびこれらのイベントはすべて独立しています。つまり、健康を維持する確率は

$$

$$(1-\beta)^{I^{(t)}}.$$

実際、これらの仮定について議論することはたくさんあります。ここで最も驚くべきことは、私の個人的な意見では、$$$y^{(t)}$..。感染者を検出する可能性のあるコインを投げるのは絶対に正常ですが、すべてのステップでこのコインをもう一度投げるのは現実的ではありません。つまり、すでに検出された感染者を「忘れる」ことができます。その結果、SIRモデルは完全に非単調なシーケンスを生成できます（多くの場合、生成します）。$$$\boldsymbol{y}$;これは奇妙なことですが、結果に大きな影響を与えることはないようであり、このプロセスをより現実的にモデル化することははるかに困難です。



さらに、このモデルは、すべての人がすべての人と「通信」する閉鎖的な人口を対象としていることは明らかです。したがって、たとえば、パラメータNが1億のロシア、またはパラメータが1,000万のモスクワ（および計算上は機能しません）。 SIRモデルの拡張と拡張の重要な領域はこれに専念しています：相互作用と起こり得る感染のより現実的なグラフを追加する方法;これについては、おそらく最後の最後の投稿で説明します。



しかし、これらすべての簡略化により、上記のパラメーターを使用して、状態間の遷移の確率行列を書き出すことができます。これらの確率（より正確には、感染の確率）は、人口の一般的な統計に依存します。を除くすべての人の状態のベクトルを指定しましょう$$$x_j$、全体 $$$\boldsymbol{x}_{-j}$、および同じ表記を他のすべての変数に拡張します。例えば、$$$I_{-j}^{(t)}$ 一度に感染した数ですか $$$t$、 言うまでもなく $$$x_j$..。次に、からの移行の確率について$$$x_j^{(t-1)}$ で $$$x_j^{(t)}$ 我々が得る

$$

$$p\left(x_j^{(t)}=S\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=R\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = \mu,$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - \mu,$$

そして他のすべての場合

$$

$$p\left(x_j^{(t)}\mid x_j^{(t-1)}, \boldsymbol{x}_{-j}^{(t-1)}\right) = 0.$$

同じことを遷移確率行列の形式でより明確に書くことができます（行と列の順序は自然です、SIR）：

$$

$$\left(\begin{matrix} (1 - \beta)^{I_{-j}^{(t-1)}} & 1 - (1 - \beta)^{I_{-j}^{(t-1)}} & 0 \\ 0 & 1 - \mu & \mu \\ 0 & 0 & 1\end{matrix}\right)$$

マルコフチェーンとマルコフモデルに精通している読者には、これは単なる隠されたマルコフモデルのように見えるかもしれません。隠された状態があり、隠された状態ごとに観測可能なものが明確に分布しています。遷移は実際にはマルコフです。つまり、次の隠された状態は前の状態にのみ依存します...しかし、 、彼らが言うように、1つの注意点があります：遷移確率は一定とは見なされません、それらは変化とともに変化します$$$I^{(t)}$これはモデルの非常に重要な側面であり、捨てることはできません。



したがって、このモデルでの推論は、通常の隠されたマルコフモデルよりも突然はるかに困難になります（ただし、そのような贈り物が常にあるとは限りません）。しかし、結論はもっと複雑ですが、それでも人間の心に左右されます-次のインスタレーション（もしあれば）でこれについてお話します。そして今日は、ほぼ十分です。少しリラックスして、これまでのところ生成的な意味でこのモデルで遊んでみましょう。

データ生成の例

偉大な愛好家および専門家として、

内向者は検疫に入りました。

***

「私は家で働くことができませんでした」と

蜂はワームに説明しようとしました。

***

カガノフは陽気に冗談を言って死んだ。

もちろん、彼には大変申し訳ありませんが...



レオニードカガノフ。検疫

モデルのパラメーターがわかっていて、集団内での病気の広がりがどのように進展するかについての軌跡を生成する必要がある場合、SIRでは複雑なことは何もありません。以下のコードは、モデルに従って母集団の例を生成します。私がコーディングした状態$$$S=0$、 $$$I=1$、 $$$R=2$..。私が警告したように、簡単にするために、私は現時点でそれを仮定します$$$t=0$ 人口の中にちょうど一人の病気の人がいて、それからそれは続きます。

def sample_population(N, T, true_rho, true_beta, true_mu):
    true_log1mbeta = np.log(1 - true_beta)

    cur_states = np.zeros(N)
    cur_states[:1] = 1
    cur_I, test_y, true_statistics = 1, [1], [[N-1, 1, 0]]

    for t in range(T):
        logprob_stay_healthy = cur_I * true_log1mbeta
        for i in range(N):
            if cur_states[i] == 0 and np.random.rand() < -np.expm1(logprob_stay_healthy):
                cur_states[i] = 1
            elif cur_states[i] == 1 and np.random.rand() < true_mu:
                cur_states[i] = 2

        cur_I = np.sum(cur_states == 1)
        test_y.append( np.random.binomial( cur_I, true_rho ) )
        true_statistics.append([np.sum(cur_states == 0), np.sum(cur_states == 1), np.sum(cur_states == 2)])

    return test_y, np.array(true_statistics).T

N, T, true_rho, true_beta, true_mu = 100, 20, 0.1, 0.05, 0.1
test_y, true_statistics = sample_population(N, T, true_rho, true_beta, true_mu)

このコードは実際のデータだけでなく $$$\boldsymbol{y}$だけでなく、「真の」統計 $$$S^{(t)}$、 $$$I^{(t)}$、 $$$R^{(t)}$視覚化できるように。やってみましょう; パラメータ用$$$N=100$、 $$$T=20$、 $$$\rho=0.1$、 $$$\beta=0.2$、 $$$\mu=0.3$あなたはこのようなものを得ることができます：







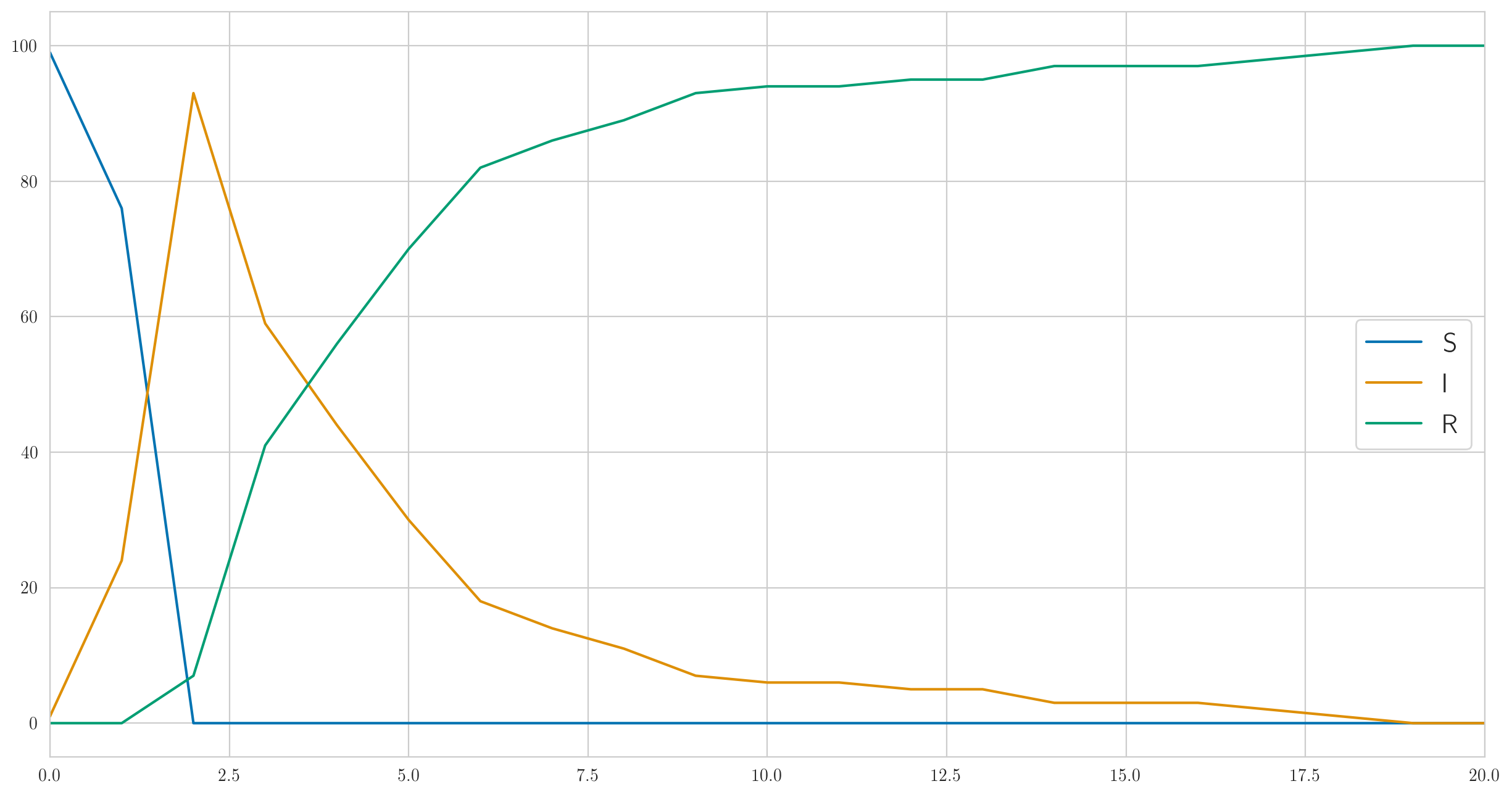
あなたが見ることができるように、この例では、誰もが非常に速く病気になり、そしてゆっくりと良くなり始めます。そして、病気で実際に観察されたデータは次のようになります。

[1 6 13 6 6 4 1 0 0 1 0 1 2 0 0 0 0 0 1 0 0]

上で説明したように、ここには単調さがないことに注意してください。



しかし、これは確かに唯一の可能な動作ではありません。感染が十分に速く、病気が私たちのテスト集団の100人全員をほぼ即座にカバーするように、上記のパラメーターを選択しました。そしてあなたがそうするなら$$$\beta$ 小さい、例えば $$$\beta=0.01$、その後、感染ははるかに遅くなり、最後の病気の人が回復して滞在しなくなる前に、誰もが病気になる時間がないでしょう。このようなもの：







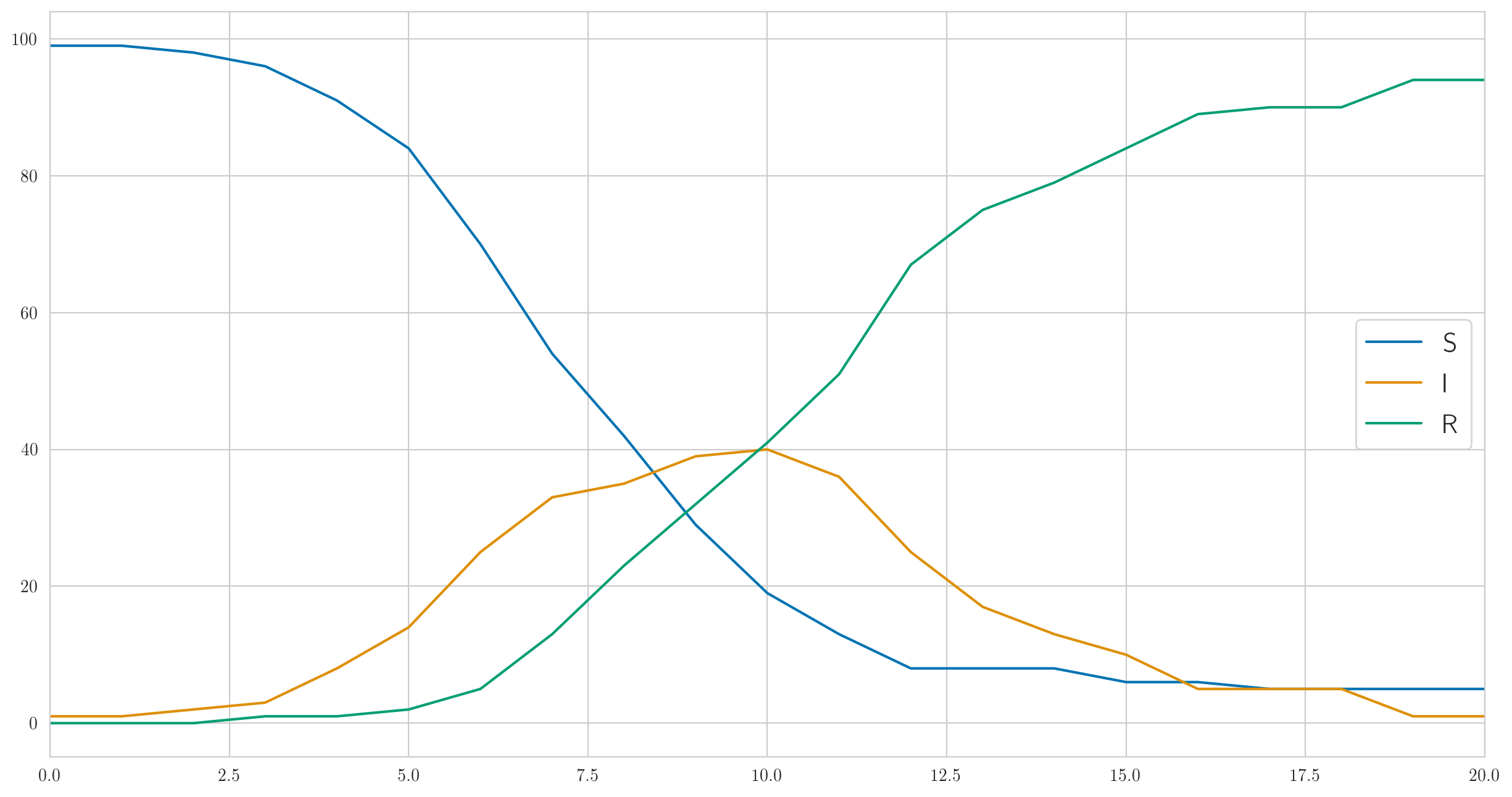
そして、検出されたケースの数も完全に異なります：

[1 0 0 0 0 1 2 2 3 1 1 9 3 1 3 1 0 1 0 0 0]

病気をさらに「絞める」ことは可能です。たとえば、去りましょう$$$\beta=0.01$しかし置く $$$\mu=0.5$つまり、各時間間隔で、各病気の人は0.5ずつ回復する可能性があります（最終的に、これは論理的です：彼が回復するかどうかのどちらかです）。そうすると、100人のうち50〜60人だけがひどいウイルスに病気になります。曲線は次のようになります。

[1 0 0 1 3 2 1 1 0 3 0 0 0 0 0 1 0 0 0 0 0]

しかし、もちろん、全体像はどのような場合でもほぼ同じように見えます。最初は指数関数的な成長、次に飽和状態への出口です。唯一の違いは、全員が再起動する前に最後のキャリアが回復する時間があるかどうかです。



さて、中間結果を要約する時が来ました。今日、私たちは最も単純な疫学的モデルの1つがどのように見えるかを見てきました。多くの単純化された仮定にもかかわらず、SIRモデルはこの形式でも非常に有用です。事実、その拡張のほとんどはかなり単純であり、問​​題の一般的な本質を変えることはありません。したがって、続行する場合は、次のシリーズでSIRモデルをトレーニングする方法について説明します。ただし、これには非常に多くの興味深いことが含まれるため、おそらく1つの投稿にも収まりません。次回まで！