
みなさん、こんにちは。今日はJPEG圧縮アルゴリズムを扱います。多くの人は、JPEGがアルゴリズムほどのフォーマットではないことを知りません。表示されるJPEG画像のほとんどはJFIF(JPEG File Interchange Format)であり、その中にJPEG圧縮アルゴリズムが適用されています。記事の終わりまでに、このアルゴリズムがデータを圧縮する方法と、Pythonで解凍コードを作成する方法についての理解が深まります。JPEG形式のすべてのニュアンス(たとえば、プログレッシブスキャン)については考慮しませんが、独自のデコーダーを作成している間は、形式の基本的な機能についてのみ説明します。
前書き
すでに何百もの記事が書かれているのに、なぜJPEGに別の記事を書くのですか?通常、そのような記事では、著者はフォーマットが何であるかについてのみ話します。開梱とデコードのコードは記述しません。そして、あなたが何かを書いたとしても、それはC / C ++になり、このコードは幅広い人々がアクセスできなくなります。この伝統を打ち破り、Python3で基本的なJPEGデコーダーがどのように機能するかを示したいと思います。MITが開発したこのコードに基づいていますが、読みやすさと明確さのために大幅に変更します。この記事の変更されたコードは、私のリポジトリにあります。
JPEGのさまざまな部分
アンジュ・アルベルティーニが 作った写真から始めましょう。単純なJPEGファイルのすべての部分が一覧表示されます。各セグメントを分析し、記事を読むと、この図に何度も戻ります。
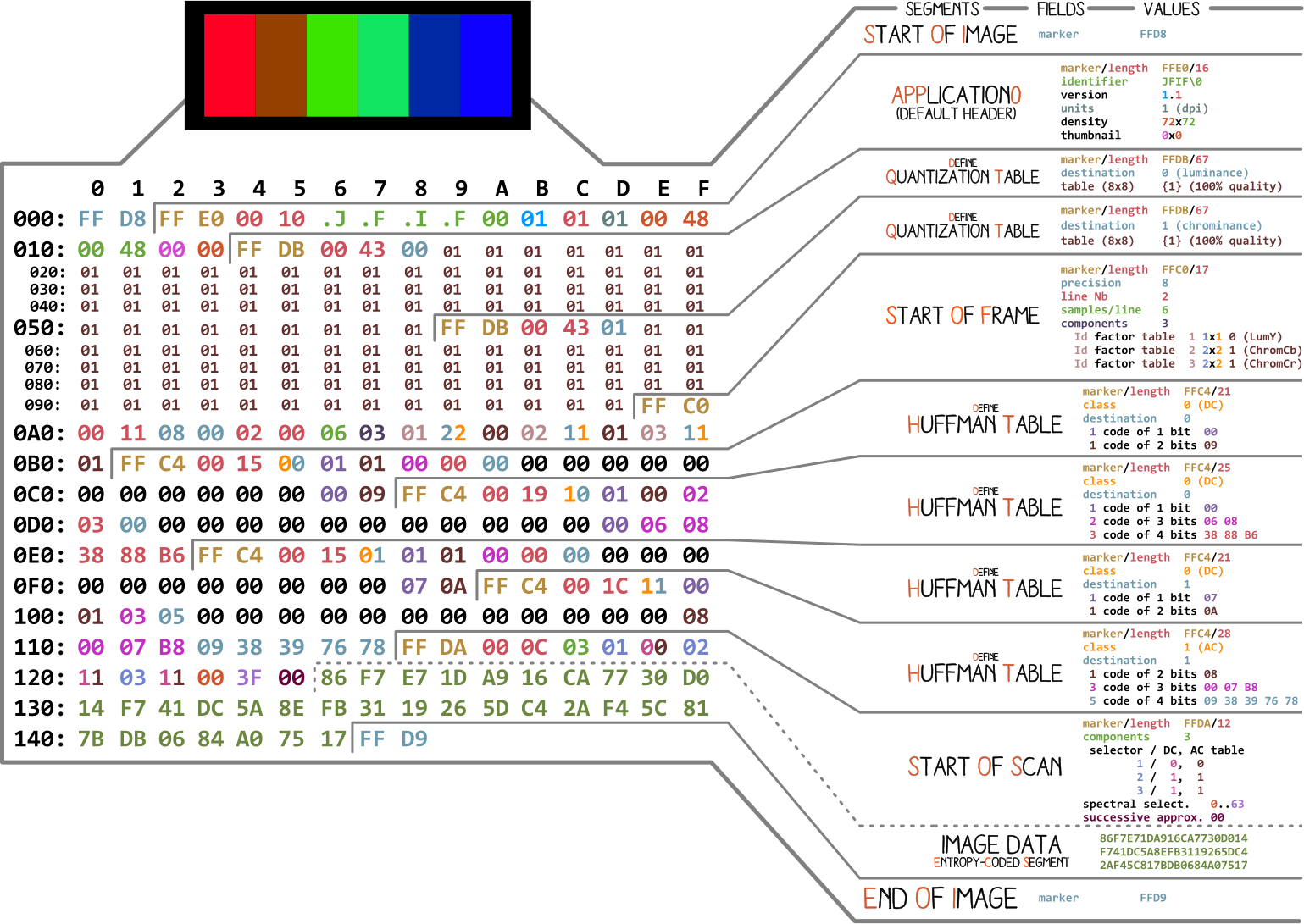
ほとんどすべてのバイナリファイルには、いくつかのマーカー(またはヘッダー)が含まれています。それらはある種のブックマークと考えることができます。これらはファイルの操作に不可欠であり、ファイル(MacおよびLinuxの場合)などのプログラムによって使用され、ファイルの詳細を確認できます。マーカーは、特定の情報がファイルのどこに保存されているかを正確に示します。ほとんどの場合、マーカーは
length特定のセグメントの長さ()に従って配置されます。
ファイルの開始と終了
私たちにとって重要な最初のマーカーは
FF D8です。画像の始まりを定義します。見つからない場合は、マーカーが他のファイルにあると見なすことができます。マーカーはそれほど重要ではありませんFF D9。画像ファイルの最後に到達したと表示されます。範囲FFD0-FFD9とFF01、を除いて、各マーカーの後に、このマーカーのセグメント長の値がすぐに表示されます。また、ファイルの最初と最後のマーカーは常に2バイトの長さです。
この画像を使用します。

開始マーカーと終了マーカーを見つけるためのコードを書いてみましょう。
from struct import unpack
marker_mapping = {
0xffd8: "Start of Image",
0xffe0: "Application Default Header",
0xffdb: "Quantization Table",
0xffc0: "Start of Frame",
0xffc4: "Define Huffman Table",
0xffda: "Start of Scan",
0xffd9: "End of Image"
}
class JPEG:
def __init__(self, image_file):
with open(image_file, 'rb') as f:
self.img_data = f.read()
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
elif marker == 0xffda:
data = data[-2:]
else:
lenchunk, = unpack(">H", data[2:4])
data = data[2+lenchunk:]
if len(data)==0:
break
if __name__ == "__main__":
img = JPEG('profile.jpg')
img.decode()
# OUTPUT:
# Start of Image
# Application Default Header
# Quantization Table
# Quantization Table
# Start of Frame
# Huffman Table
# Huffman Table
# Huffman Table
# Huffman Table
# Start of Scan
# End of Image
イメージのバイトを解凍するために、structを使用しました。
>H告げるstructデータ型読み取るためにそれをunsigned shortビッグエンディアン順に彼らと仕事を。 JPEGデータは、最高から最低の形式で保存されます。 EXIFデータのみをリトルエンディアン形式にすることができます(ただし、通常はそうではありません)。また、サイズshortは2なので、unpackから2バイトを転送しますimg_data。それが何であるかをどうやって知りましたかshort?マーカーがJPEGであることがわかっているので、4つの16進文字で示されますffd8。そのような1文字は4ビット(1/2バイト)に相当するため、4文字はshort。と同様に2バイトに相当します。
[スキャンの開始]セクションの直後に、特定の長さを持たないスキャンされた画像データが続きます。これらはファイルマーカーの終わりまで続くため、今のところ、スキャン開始マーカーが見つかったら手動で「検索」します。
それでは、残りの画像データを扱いましょう。これを行うには、最初に理論を研究し、次にプログラミングに移ります。
JPEGエンコーディング
まず、JPEGで使用される基本的な概念とコーディング手法について説明します。また、コーディングは逆の順序で行われます。私の経験では、デコードはそれなしでは理解するのが難しいでしょう。
以下の図はまだ明確ではありませんが、エンコードとデコードのプロセスを学習するときにヒントを提供します。JPEGエンコーディングの手順は次のとおりです(ソース)。
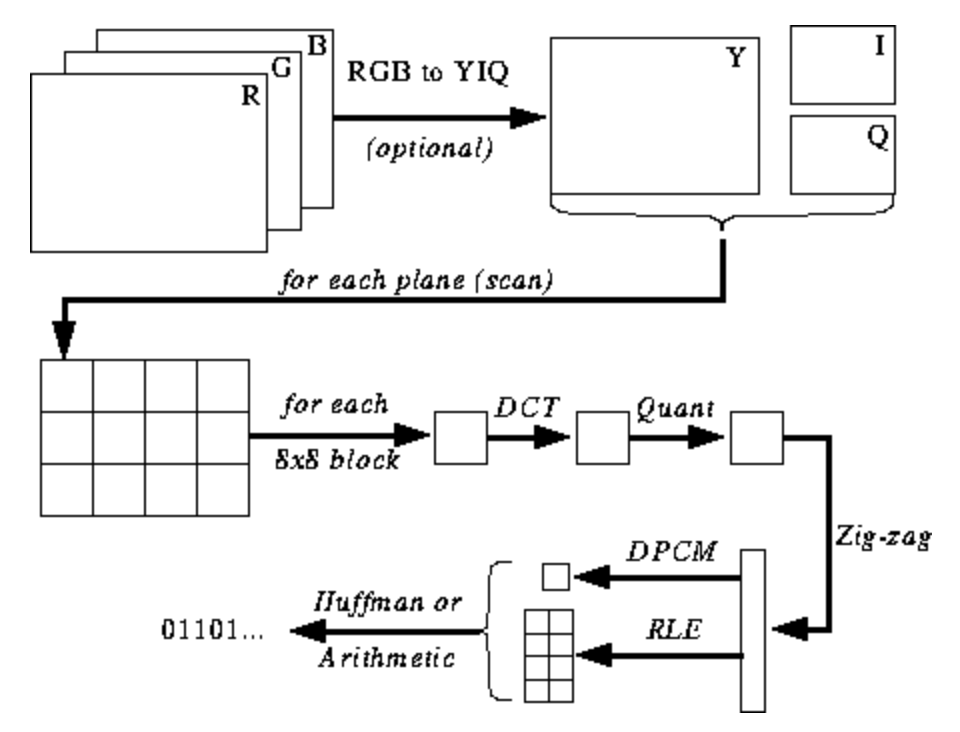
JPEGカラースペース
JPEG仕様(ISO / IEC 10918-6:2013(E)セクション6.1)によると:
- 1つのコンポーネントのみでエンコードされた画像は、グレースケールデータとして扱われます。ここで、0は黒、255は白です。
- 3つのコンポーネントでエンコードされた画像は、YCbCr空間でエンコードされたRGBデータと見なされます。セクション6.5.3で説明されているAPP14マーカーセグメントが画像に含まれている場合、APP14マーカーセグメントの情報に従って、色分けはRGBまたはYCbCrと見なされます。RGBとYCbCrの関係は、ITU-T T.871 |に従って定義されています。ISO / IEC10918-5。
- , , CMYK-, (0,0,0,0) . APP14, 6.5.3, CMYK YCCK APP14. CMYK YCCK 7.
JPEGアルゴリズムのほとんどの実装では、RGBの代わりに輝度とクロミナンス(YUVエンコーディング)を使用します。人間の目は小さな領域の明るさの高周波変化を区別するのが非常に苦手なので、これは非常に便利です。そのため、周波数を下げることができ、人は違いに気付かないでしょう。それは何をするためのものか?品質の低下がほとんど感じられない、高度に圧縮された画像。
RGBと同様に、各ピクセルは3バイトの色(赤、緑、青)でエンコードされるため、YUVでは3バイトが使用されますが、その意味は異なります。 Yコンポーネントは、色の明るさ(輝度、または輝度)を定義します。 UとVは色(彩度)を定義します。Uは青い部分を担当し、Vは赤い部分を担当します。
このフォーマットは、テレビがまだそれほど一般的ではなかった時代に開発されたもので、エンジニアはカラーと白黒のテレビ放送の両方に同じ画像エンコーディングフォーマットを使用したいと考えていました。これについて詳しくは、こちらをご覧ください。
離散コサイン変換と量子化
JPEGは、画像を8x8ブロックのピクセル(MCU、最小コーディングユニットと呼ばれます)に変換し、中心が0になるようにピクセル値の範囲を変更してから、各ブロックに離散余弦変換を適用し、量子化を使用して結果を圧縮します。これが何を意味するのか見てみましょう。
ディスクリートコサイン変換(DCT)は、ディスクリートデータをコサイン波の組み合わせに変換する方法です。写真をコサインのセットに変換することは、一見無駄な練習のように見えますが、次のステップについて学ぶとその理由がわかります。 DCTは8x8ピクセルのブロックを取り、8x8の余弦関数のマトリックスを使用してそのブロックを再現する方法を説明します。詳細はこちら。
マトリックスは次のようになります。

DCTは各ピクセルコンポーネントに個別に適用されます。その結果、係数の8x8マトリックスが得られます。これは、入力8x8マトリックス内の(64個すべての)コサイン関数の寄与を示しています。 DCT係数のマトリックスでは、最大値は通常左上隅にあり、最小値は右下隅にあります。左上が最低周波数の余弦関数で、右下が最高です。
これは、ほとんどの画像に大量の低周波情報があり、高周波情報の割合が少ないことを意味します。各DCTマトリックスの右下のコンポーネントに値0が割り当てられている場合、人は高周波の変化をうまく区別できないため、結果の画像は同じように見えます。これは、次のステップで行うことです。
このトピックに関するすばらしいビデオを見つけました。PrEPの意味がわからない場合は、次を確認してください。
JPEGが損失の多い圧縮アルゴリズムであることは誰もが知っています。しかし、これまでのところ、私たちは何も失っていません。情報を失うことなく、8x8コサイン関数のブロックに変換された8x8YUVコンポーネントのブロックのみがあります。データ損失の段階は量子化です。
量子化は、特定の範囲から2つの値を取得し、それらを個別の値に変換するプロセスです。私たちの場合、これは、結果のDCTマトリックスの最高周波数係数を0に減らすための単なる名前です。JPEGを使用して画像を保存する場合、ほとんどの画像エディタでは、設定する圧縮レベルを尋ねられます。これは、高周波情報の損失が発生する場所です。結果のJPEG画像から元の画像を再作成することはできなくなります。
圧縮率に応じて異なる量子化マトリックスが使用されます(面白い事実:ほとんどの開発者は量子化テーブルを作成するための特許を持っています)。係数のDCTマトリックスを要素ごとに量子化マトリックスで除算し、結果を整数に丸めて、量子化されたマトリックスを取得します。
例を見てみましょう。そのようなDCTマトリックスがあるとしましょう:

そして、これが通常の量子化マトリックスです。
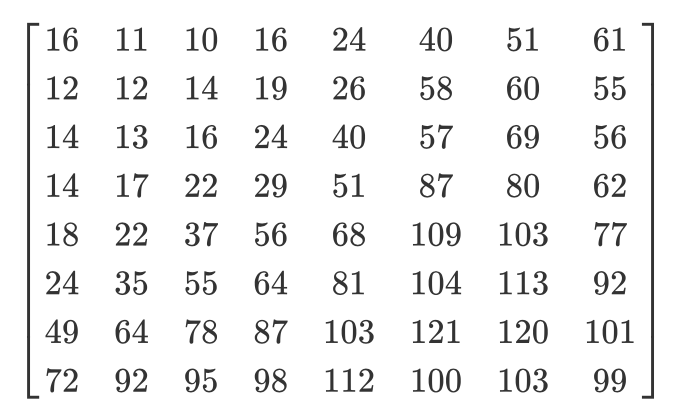
量子化されたマトリックスは次のようになります。

人間は高周波情報を見ることができませんが、8x8ピクセルのブロックから多くのデータを削除すると、画像が粗くなりすぎます。このような量子化されたマトリックスでは、最初の値はDC値と呼ばれ、他のすべての値はAC値と呼ばれます。すべての量子化されたマトリックスのDC値を取得して新しい画像を生成した場合、元の画像の8分の1の解像度でプレビューが表示されます。
また、量子化を使用したため、色が[0.255]の範囲内にあることを確認する必要があることにも注意してください。それらが飛び出す場合は、手動でこの範囲に移動する必要があります。
ジグザグ
量子化後、JPEGアルゴリズムはジグザグスキャンを使用してマトリックスを1次元形式に変換します。
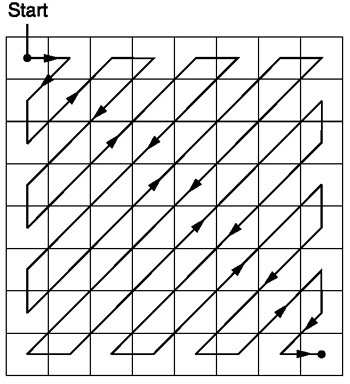
ソース。
このような量子化されたマトリックスを作成しましょう。
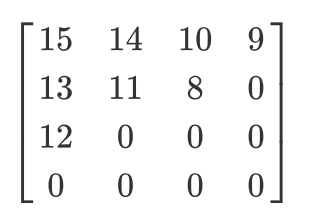
その場合、ジグザグスキャンの結果は次のようになります。
[15 14 13 12 11 10 9 8 0 ... 0]
量子化後、ほとんどの低周波(最も重要な)情報がマトリックスの先頭に配置され、ジグザグスキャンがこのデータを1次元マトリックスの先頭に格納するため、このコーディングが推奨されます。これは、次のステップである圧縮に役立ちます。
ランレングスコーディングとデルタコーディング
ランレングスエンコーディングは、反復データを圧縮するために使用されます。ジグザグスキャンの後、配列の最後にほとんどゼロがあることがわかります。長さのエンコードにより、この無駄なスペースを利用し、使用するバイト数を減らしてすべてのゼロを表すことができます。次のデータがあるとしましょう。
10 10 10 10 10 10 10
シリーズの長さをエンコードした後、次のようになります。
7 10
7バイトを2バイトに圧縮しました。
デルタエンコーディングは、その前のバイトを基準にしたバイトを表すために使用されます。例を挙げて説明する方が簡単です。次のデータを用意しましょう。
10 11 12 13 10 9
デルタコーディングを使用すると、次のように表すことができます。
10 1 2 3 0 -1
JPEGでは、DCTマトリックスの各DC値は、前のDC値に対してデルタエンコードされます。これは、画像の最初のDCT係数を変更することにより、全体像を破壊することを意味します。ただし、最後のDCTマトリックスの最初の値を変更すると、画像の非常に小さなフラグメントにのみ影響します。
通常、画像の最初のDC値が最も変化するため、このアプローチは便利です。デルタコーディングを使用して、残りのDC値を0に近づけ、ハフマンコーディングによる圧縮を改善します。
ハフマンコーディング
無損失の圧縮方法です。ある日、ハフマンは「フリーテキストを保存するために使用できるビットの最小数はいくつですか?」と疑問に思いました。その結果、エンコード形式が作成されました。テキストがあるとしましょう:
a b c d e
通常、各文字は1バイトのスペースを占有します。
a: 01100001
b: 01100010
c: 01100011
d: 01100100
e: 01100101
これがバイナリASCIIエンコーディングの原理です。マッピングを変更するとどうなりますか?
# Mapping
000: 01100001
001: 01100010
010: 01100011
100: 01100100
011: 01100101
同じテキストを保存するために必要なビット数が大幅に減りました。
a: 000
b: 001
c: 010
d: 100
e: 011
それはすべてうまくいっていますが、さらに多くのスペースを節約する必要がある場合はどうなりますか?たとえば、次のようになります。
# Mapping
0: 01100001
1: 01100010
00: 01100011
01: 01100100
10: 01100101
a: 0
b: 1
c: 00
d: 01
e: 10
ハフマンコーディングは、そのような可変長のマッチングを可能にします。入力データが取得され、最も一般的な文字はビットの小さな組み合わせと照合され、頻度の低い文字は大きな組み合わせと照合されます。そして、結果のマッピングはバイナリツリーに収集されます。 JPEGでは、ハフマンコーディングを使用してDCT情報を保存します。 DC値のデルタコーディングによりハフマンコーディングが容易になると述べたことを覚えていますか?その理由をご理解いただければ幸いです。デルタエンコーディングの後、一致する「文字」が少なくなり、ツリーサイズが小さくなります。
トムスコットは、ハフマンアルゴリズムがどのように機能するかを説明する素晴らしいビデオを持っています。読む前に見てください。
JPEGには、最大4つのハフマンテーブルが含まれ、これらは「ハフマンテーブルの定義」(で始まる
0xffc4)に格納されます。 DCT係数は、2つの異なるハフマンテーブルに格納されます。1つはジグザグテーブルのDC値、もう1つはジグザグテーブルのAC値です。これは、コーディング時に、2つのマトリックスからのDC値とAC値を組み合わせる必要があることを意味します。輝度チャネルと色度チャネルのDCT情報は別々に保存されるため、2セットのDC情報と2セットのAC情報、合計4つのハフマンテーブルがあります。
画像がグレースケールの場合、色は必要ないため、ハフマンテーブルは2つ(DC用とAC用)しかありません。ご存知かもしれませんが、2つの異なる画像は非常に異なるハフマンテーブルを持つ可能性があるため、各JPEG内に保存することが重要です。
これで、JPEG画像の主な内容がわかりました。デコードに移りましょう。
JPEGデコード
デコードは次の段階に分けることができます。
- ハフマンテーブルの抽出とビットのデコード。
- ランレングスおよびデルタコーディングのロールバックを使用してDCT係数を抽出します。
- DCT係数を使用して余弦波を組み合わせ、各8x8ブロックのピクセル値を再構築します。
- ピクセルごとにYCbCrをRGBに変換します。
- 結果のRGB画像を表示します。
JPEG標準は、次の4つの圧縮形式をサポートしています。
- ベース
- 拡張シリアル
- プログレッシブ
- 損失なし
基本的な圧縮を使用します。これには、互いに続く一連の8x8ブロックが含まれています。他の形式では、データテンプレートはわずかに異なります。明確にするために、画像の16進数のコンテンツのさまざまなセグメントに色を付けました。
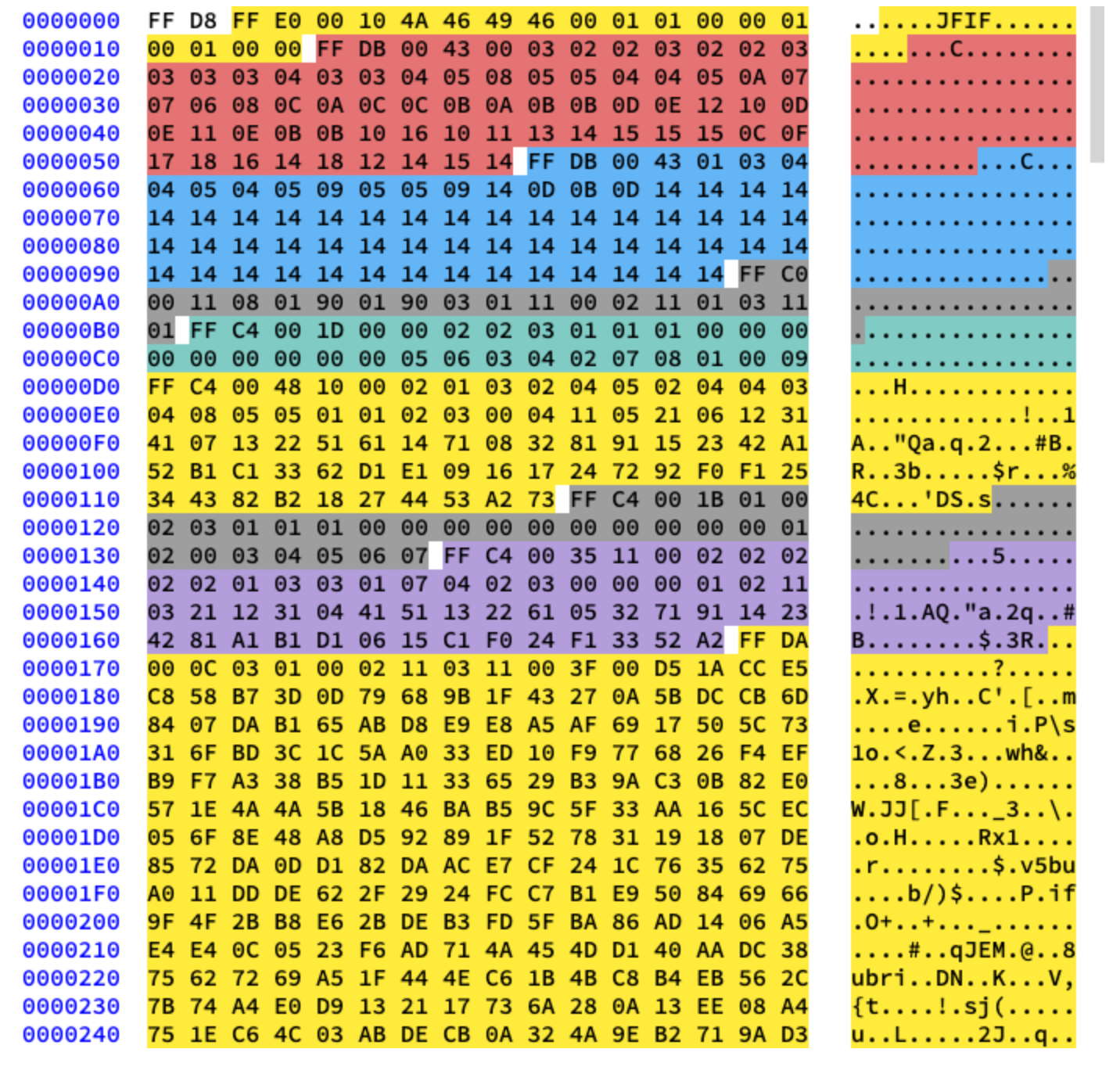
ハフマンテーブルの抽出
JPEGには4つのハフマンテーブルが含まれていることはすでにわかっています。これが最後のエンコーディングなので、それを使用してデコードを開始します。表の各セクションには、次の情報が含まれています。
| フィールド | サイズ | 説明 |
|---|---|---|
| マーカーID | 2バイト | 0xffおよび0xc4はDHTを識別します |
| 長さ | 2バイト | テーブルの長さ |
| ハフマンテーブル情報 | 1バイト | ビット0 ... 3:テーブルの数(0 ... 3、それ以外の場合はエラー)ビット4:テーブルのタイプ、0 = DCテーブル、1 = ACテーブルビット5 ... 7:使用しない、0である必要があります |
| キャラクター | 16バイト | コードの長さが1 ... 16の文字数、これらのバイトの合計(n)は、<= 256でなければならないコードの総数です。 |
| シンボル | nバイト | この表には、コード長の昇順で文字が含まれています(n =コードの総数)。 |
次のようなハフマンテーブルがあるとしましょう(ソース):
| シンボル | ハフマンコード | コードの長さ |
|---|---|---|
| a | 00 | 2 |
| b | 010 | 3 |
| c | 011 | 3 |
| d | 100 | 3 |
| e | 101 | 3 |
| f | 110 | 3 |
| g | 1110 | 4 |
| h | 11110 | 五 |
| 私 | 111110 | 6 |
| j | 1111110 | 7 |
| k | 11111110 | 8 |
| l | 111111110 | ナイン |
これは、次のようなJFIFファイルに保存されます(バイナリ形式。わかりやすくするためにASCIIを使用しています)。
0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0 a b c d e f g h i j k l
0は、長さ1のハフマンコードがないことを意味します。1は、長さ2のハフマンコードが1つあることを意味します。DHTセクションでは、クラスとIDの直後に、データは常に16バイトの長さです。DHTから長さと要素を抽出するコードを書いてみましょう。
class JPEG:
# ...
def decodeHuffman(self, data):
offset = 0
header, = unpack("B",data[offset:offset+1])
offset += 1
# Extract the 16 bytes containing length data
lengths = unpack("BBBBBBBBBBBBBBBB", data[offset:offset+16])
offset += 16
# Extract the elements after the initial 16 bytes
elements = []
for i in lengths:
elements += (unpack("B"*i, data[offset:offset+i]))
offset += i
print("Header: ",header)
print("lengths: ", lengths)
print("Elements: ", len(elements))
data = data[offset:]
def decode(self):
data = self.img_data
while(True):
# ---
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
data = data[len_chunk:]
if len(data)==0:
break
コードを実行すると、次のようになります。
Start of Image
Application Default Header
Quantization Table
Quantization Table
Start of Frame
Huffman Table
Header: 0
lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 10
Huffman Table
Header: 16
lengths: (0, 2, 1, 3, 2, 4, 5, 2, 4, 4, 3, 4, 8, 5, 5, 1)
Elements: 53
Huffman Table
Header: 1
lengths: (0, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 8
Huffman Table
Header: 17
lengths: (0, 2, 2, 2, 2, 2, 1, 3, 3, 1, 7, 4, 2, 3, 0, 0)
Elements: 34
Start of Scan
End of Image
優れた!長さと要素があります。次に、取得した長さと要素からバイナリツリーを再構築するために、独自のハフマンテーブルクラスを作成する必要があります。ここからコードをコピーします:
class HuffmanTable:
def __init__(self):
self.root=[]
self.elements = []
def BitsFromLengths(self, root, element, pos):
if isinstance(root,list):
if pos==0:
if len(root)<2:
root.append(element)
return True
return False
for i in [0,1]:
if len(root) == i:
root.append([])
if self.BitsFromLengths(root[i], element, pos-1) == True:
return True
return False
def GetHuffmanBits(self, lengths, elements):
self.elements = elements
ii = 0
for i in range(len(lengths)):
for j in range(lengths[i]):
self.BitsFromLengths(self.root, elements[ii], i)
ii+=1
def Find(self,st):
r = self.root
while isinstance(r, list):
r=r[st.GetBit()]
return r
def GetCode(self, st):
while(True):
res = self.Find(st)
if res == 0:
return 0
elif ( res != -1):
return res
class JPEG:
# -----
def decodeHuffman(self, data):
# ----
hf = HuffmanTable()
hf.GetHuffmanBits(lengths, elements)
data = data[offset:]
GetHuffmanBits長さと要素を受け取り、要素を繰り返し処理して、リストに入れますroot。これはバイナリツリーであり、ネストされたリストが含まれています。ハフマンツリーがどのように機能し、Pythonでそのようなデータ構造を作成する方法をインターネットで読むことができます。最初のDHT(記事の冒頭の写真から)には、次のデータ、長さ、要素があります。
Hex Data: 00 02 02 03 01 01 01 00 00 00 00 00 00 00 00 00
Lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: [5, 6, 3, 4, 2, 7, 8, 1, 0, 9]
呼び出し後、
GetHuffmanBitsリストrootには次のデータが含まれます。
[[5, 6], [[3, 4], [[2, 7], [8, [1, [0, [9]]]]]]]
HuffmanTableまたGetCode、ツリーをウォークスルーし、ハフマンテーブルを使用してデコードされたビットを返すメソッドも含まれています。このメソッドは、入力としてビットストリームを受け取ります。これは、データのバイナリ表現にすぎません。たとえば、のビットストリームはにabcなります011000010110001001100011。まず、各文字をASCIIコードに変換し、それをバイナリに変換します。文字列をビットに変換し、ビットを1つずつカウントするのに役立つクラスを作成しましょう。
class Stream:
def __init__(self, data):
self.data= data
self.pos = 0
def GetBit(self):
b = self.data[self.pos >> 3]
s = 7-(self.pos & 0x7)
self.pos+=1
return (b >> s) & 1
def GetBitN(self, l):
val = 0
for i in range(l):
val = val*2 + self.GetBit()
return val
初期化するとき、クラスにバイナリデータを与えてから、とを使用
GetBitしてそれを読み取りますGetBitN。
量子化テーブルのデコード
[量子化テーブルの定義]セクションには、次のデータが含まれています。
| フィールド | サイズ | 説明 |
|---|---|---|
| マーカーID | 2バイト | 0xffおよび0xdbはDQTセクションを識別します |
| 長さ | 2バイト | 量子化テーブルの長さ |
| 定量化情報 | 1バイト | ビット0 ... 3:量子化テーブルの数(0 ... 3、それ以外の場合はエラー)ビット4 ... 7:量子化テーブルの精度、0 = 8ビット、それ以外の場合は16ビット |
| バイト | nバイト | 量子化テーブルの値、n = 64 *(精度+ 1) |
JPEG規格によると、デフォルトのJPEG画像には、輝度と彩度の2つの量子化テーブルがあります。それらはマーカーで始まります
0xffdb。コードの結果には、すでに2つのそのようなマーカーが含まれています。量子化テーブルをデコードする機能を追加しましょう。
def GetArray(type,l, length):
s = ""
for i in range(length):
s =s+type
return list(unpack(s,l[:length]))
class JPEG:
# ------
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
with open(image_file, 'rb') as f:
self.img_data = f.read()
def DefineQuantizationTables(self, data):
hdr, = unpack("B",data[0:1])
self.quant[hdr] = GetArray("B", data[1:1+64],64)
data = data[65:]
def decodeHuffman(self, data):
# ------
for i in lengths:
elements += (GetArray("B", data[off:off+i], i))
offset += i
# ------
def decode(self):
# ------
while(True):
# ----
else:
# -----
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
data = data[len_chunk:]
if len(data)==0:
break
最初にメソッドを定義しました
GetArray。これは、バイナリデータから可変数のバイトをデコードするための便利な手法です。またdecodeHuffman、新しい関数を利用するために、メソッドの一部のコードを置き換えました。次に、メソッドが定義されましたDefineQuantizationTables。量子化テーブルを含むセクションのタイトルを読み取り、ヘッダーの値をキーとして使用して、量子化データを辞書に適用します。この値は、輝度の場合は0、色度の場合は1にすることができます。JFIFの量子化テーブルを持つ各セクションには、64バイトのデータが含まれています(8x8量子化マトリックスの場合)。
画像の量子化行列を出力すると、次のようになります。
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
3 2 2 3 2 2 3 3
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
フレームの開始をデコードする
[フレームの開始]セクションには、次の情報が含まれています(ソース)。
| フィールド | サイズ | 説明 |
|---|---|---|
| マーカーID | 2バイト | 0xff 0xc0 SOF |
| 2 | 8 + *3 | |
| 1 | , 8 (12 16 ). | |
| 2 | > 0 | |
| 2 | > 0 | |
| 1 | 1 = , 3 = YcbCr YIQ | |
| 3 | 3 . (1 ) (1 = Y, 2 = Cb, 3 = Cr, 4 = I, 5 = Q), (1 ) ( 0...3 , 4...7 ), (1 ). |
ここでは、すべてに関心があるわけではありません。画像の幅と高さ、および各コンポーネントの量子化テーブルの数を抽出します。幅と高さは、[スキャンの開始]セクションから画像の実際のスキャンのデコードを開始するために使用されます。主にYCbCrイメージを使用するため、3つのコンポーネントがあり、それらのタイプはそれぞれ1、2、および3であると想定できます。このデータをデコードするコードを書いてみましょう。
class JPEG:
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
self.quantMapping = []
with open(image_file, 'rb') as f:
self.img_data = f.read()
# ----
def BaselineDCT(self, data):
hdr, self.height, self.width, components = unpack(">BHHB",data[0:6])
print("size %ix%i" % (self.width, self.height))
for i in range(components):
id, samp, QtbId = unpack("BBB",data[6+i*3:9+i*3])
self.quantMapping.append(QtbId)
def decode(self):
# ----
while(True):
# -----
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
data = data[len_chunk:]
if len(data)==0:
break
JPEGクラスにlist属性を追加し、SOFセクションから必要なデータをデコードし、各コンポーネントの量子化テーブルの数をリストに入れる
quantMappingメソッドBaselineDCTを定義しましたquantMapping。「スキャンの開始」セクションを読み始めるときに、これを利用します。したがって、私たちの写真では、次のようになりますquantMapping。
Quant mapping: [0, 1, 1]
スキャン開始のデコード
これはJPEG画像の「肉」であり、画像自体のデータが含まれています。私たちは最も重要な段階に到達しました。以前にデコードしたものはすべて、画像自体をデコードするのに役立つカードと見なすことができます。このセクションには、画像自体(エンコードされたもの)が含まれています。セクションを読み、すでにデコードされたデータを使用して復号化します。
すべてのマーカーは
0xff。で始まります。この値はスキャンされた画像の一部にすることもできますが、このセクションに存在する場合は、常にとが続き0x00ます。 JPEGエンコーダーはそれを自動的に挿入します。これはバイトスタッフィングと呼ばれます。したがって、デコーダーはこれらを削除する必要があります0x00。そのような関数を含むSOSデコードメソッドから始めて、既存の関数を取り除きましょう0x00。スキャンしたセクションの写真にはありません0xffしかし、それでも便利な追加です。
def RemoveFF00(data):
datapro = []
i = 0
while(True):
b,bnext = unpack("BB",data[i:i+2])
if (b == 0xff):
if (bnext != 0):
break
datapro.append(data[i])
i+=2
else:
datapro.append(data[i])
i+=1
return datapro,i
class JPEG:
# ----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
return lenchunk+hdrlen
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
elif marker == 0xffda:
len_chunk = self.StartOfScan(data, len_chunk)
data = data[len_chunk:]
if len(data)==0:
break
以前は、マーカー
0xffdaが見つかったときにファイルの末尾を手動で検索していましたが、ファイル全体を体系的に表示できるツールができたので、マーカーの検索条件を演算子内に移動しますelse。関数RemoveFF00は、0x00後ではなく何か他のものを見つけると壊れ0xffます。関数がを見つける0xffd9とループが中断するため、予期せぬことを恐れずにファイルの終わりを検索できます。このコードを実行すると、ターミナルに新しいものは何も表示されません。
JPEGは画像を8x8のマトリックスに分割することを忘れないでください。次に、スキャンした画像データをビットストリームに変換し、8x8チャンクで処理する必要があります。クラスにコードを追加しましょう:
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk +hdrlen
データをビットストリームに変換することから始めましょう。前のDC要素と比較して、量子化マトリックスのDC要素(その最初の要素)にデルタコーディングが適用されていることを覚えていますか?したがって、我々は、初期化
oldlumdccoeff、oldCbdccoeffおよびoldCrdccoeffゼロ値で、彼らは私たちが以前のDC-要素の値を追跡するのに役立ちます、そして0は、我々が最初にDC-要素を見つけるデフォルトで設定されます。
ループ
forは奇妙に見えるかもしれません。self.height//8高さを88で割ることができる回数を示しますself.width//8。これは、幅と。と同じです。
BuildMatrix量子化テーブルを取得してパラメータを追加し、逆離散余弦変換行列を作成して、Y、Cr、およびCb行列を取得します。そして、関数はDrawMatrixそれらをRGBに変換します。
まず、クラスを作成しましょう
IDCT、次にメソッドの入力を開始しBuildMatrixます。
import math
class IDCT:
"""
An inverse Discrete Cosine Transformation Class
"""
def __init__(self):
self.base = [0] * 64
self.zigzag = [
[0, 1, 5, 6, 14, 15, 27, 28],
[2, 4, 7, 13, 16, 26, 29, 42],
[3, 8, 12, 17, 25, 30, 41, 43],
[9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
]
self.idct_precision = 8
self.idct_table = [
[
(self.NormCoeff(u) * math.cos(((2.0 * x + 1.0) * u * math.pi) / 16.0))
for x in range(self.idct_precision)
]
for u in range(self.idct_precision)
]
def NormCoeff(self, n):
if n == 0:
return 1.0 / math.sqrt(2.0)
else:
return 1.0
def rearrange_using_zigzag(self):
for x in range(8):
for y in range(8):
self.zigzag[x][y] = self.base[self.zigzag[x][y]]
return self.zigzag
def perform_IDCT(self):
out = [list(range(8)) for i in range(8)]
for x in range(8):
for y in range(8):
local_sum = 0
for u in range(self.idct_precision):
for v in range(self.idct_precision):
local_sum += (
self.zigzag[v][u]
* self.idct_table[u][x]
* self.idct_table[v][y]
)
out[y][x] = local_sum // 4
self.base = out
クラスを分析してみましょう
IDCT。 MCUを抽出すると、属性に格納されますbase。次に、メソッドを使用してジグザグスキャンをロールバックすることにより、MCUマトリックスを変換しますrearrange_using_zigzag。最後に、メソッドを呼び出して離散コサイン変換をロールバックしperform_IDCTます。
ご存知のように、DCテーブルは固定されています。 DCTがどのように機能するかについては考慮しません。これは、プログラミングよりも数学に関連しています。このテーブルをグローバル変数として保存し、値のペアを照会できます
x,y。IDCTテキストを読みやすくするために、テーブルとその計算をクラスに入れることにしました。変換されたMCUマトリックスの各要素に値が乗算されidc_variable、Y、Cr、およびCbの値が取得されます。
これは、メソッドを追加するとより明確になり
BuildMatrixます。
ジグザグテーブルを次のように変更すると、次のようになります。
[[ 0, 1, 5, 6, 14, 15, 27, 28],
[ 2, 4, 7, 13, 16, 26, 29, 42],
[ 3, 8, 12, 17, 25, 30, 41, 43],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
[ 9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54]]
この結果が得られます(小さなアーティファクトに注意してください):

そして、勇気があれば、ジグザグテーブルをさらに変更できます。
[[12, 19, 26, 33, 40, 48, 41, 34,],
[27, 20, 13, 6, 7, 14, 21, 28,],
[ 0, 1, 8, 16, 9, 2, 3, 10,],
[17, 24, 32, 25, 18, 11, 4, 5,],
[35, 42, 49, 56, 57, 50, 43, 36,],
[29, 22, 15, 23, 30, 37, 44, 51,],
[58, 59, 52, 45, 38, 31, 39, 46,],
[53, 60, 61, 54, 47, 55, 62, 63]]
その場合、結果は次のようになります。

私たちの方法を完成させましょう
BuildMatrix:
def DecodeNumber(code, bits):
l = 2**(code-1)
if bits>=l:
return bits
else:
return bits-(2*l-1)
class JPEG:
# -----
def BuildMatrix(self, st, idx, quant, olddccoeff):
i = IDCT()
code = self.huffman_tables[0 + idx].GetCode(st)
bits = st.GetBitN(code)
dccoeff = DecodeNumber(code, bits) + olddccoeff
i.base[0] = (dccoeff) * quant[0]
l = 1
while l < 64:
code = self.huffman_tables[16 + idx].GetCode(st)
if code == 0:
break
# The first part of the AC quantization table
# is the number of leading zeros
if code > 15:
l += code >> 4
code = code & 0x0F
bits = st.GetBitN(code)
if l < 64:
coeff = DecodeNumber(code, bits)
i.base[l] = coeff * quant[l]
l += 1
i.rearrange_using_zigzag()
i.perform_IDCT()
return i, dccoeff
まず、離散コサイン変換反転クラス(
IDCT())を作成します。次に、データをビットストリームに読み込み、ハフマンテーブルを使用してデコードします。
self.huffman_tables[0]そしてself.huffman_tables[1]、それぞれ、輝度及び彩度のためのDCテーブルを参照し、self.huffman_tables[16]そしてself.huffman_tables[17]それぞれ、luma及びchromaのためのACテーブルを参照します。
ビットストリームをデコードした後、関数を使用し
DecodeNumber て新しいデルタコード化されたDC係数を抽出し、それolddccoefficientに追加してデルタデコードされたDC係数を取得します。
次に、量子化マトリックスのAC値を使用して同じデコード手順を繰り返します。コードの意味
0ブロックの終わり(EOB)マーカーに到達し、停止する必要があることを示します。さらに、AC量子化テーブルの最初の部分は、先行ゼロがいくつあるかを示しています。それでは、シリーズの長さのコーディングについて覚えておきましょう。このプロセスを逆にして、それらの多くのビットをすべてスキップしましょう。クラスでは、IDCT明示的にゼロが割り当てられます。
MCUのDC値とAC値をデコードした後、MCUを変換し、を呼び出してジグザグスキャンを反転し
rearrange_using_zigzagます。次に、DCTを反転して、デコードされたMCUに適用します。
このメソッド
BuildMatrixは、反転されたDCTマトリックスとDC係数の値を返します。これは、1つの最小8x8エンコーディングユニットのみのマトリックスになることに注意してください。ファイル内の他のすべてのMCUに対してこれを実行しましょう。
画面に画像を表示する
それでは、メソッド内のコードで
StartOfScanTkinter Canvasを作成し、デコード後に各MCUを描画してみましょう。
def Clamp(col):
col = 255 if col>255 else col
col = 0 if col<0 else col
return int(col)
def ColorConversion(Y, Cr, Cb):
R = Cr*(2-2*.299) + Y
B = Cb*(2-2*.114) + Y
G = (Y - .114*B - .299*R)/.587
return (Clamp(R+128),Clamp(G+128),Clamp(B+128) )
def DrawMatrix(x, y, matL, matCb, matCr):
for yy in range(8):
for xx in range(8):
c = "#%02x%02x%02x" % ColorConversion(
matL[yy][xx], matCb[yy][xx], matCr[yy][xx]
)
x1, y1 = (x * 8 + xx) * 2, (y * 8 + yy) * 2
x2, y2 = (x * 8 + (xx + 1)) * 2, (y * 8 + (yy + 1)) * 2
w.create_rectangle(x1, y1, x2, y2, fill=c, outline=c)
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk+hdrlen
if __name__ == "__main__":
from tkinter import *
master = Tk()
w = Canvas(master, width=1600, height=600)
w.pack()
img = JPEG('profile.jpg')
img.decode()
mainloop()
関数
ColorConversionとから始めましょうClamp。ColorConversionY、Cr、Cbの値を取り、式でRGB成分に変換し、集計したRGB値を出力します。なぜそれらに128を追加するのですか?JPEGアルゴリズムの前に、DCTがMCUに適用され、カラー値から128を減算することを忘れないでください。色が元々[0.255]の範囲にあった場合、JPEGはそれらを[-128、+ 128]の範囲に配置します。デコード時にこのエフェクトをロールバックする必要があるため、RGBに128を追加します。Clamp開梱時に、結果の値は、範囲[0.255]の外に行くことが、私たちは[0.255]この範囲に保管してください。
方法で
DrawMatrixY、Cr、Cbのデコードされた各8x8マトリックスをループし、各マトリックス要素をRGB値に変換します。変換後canvas、メソッドを使用してTkinterでピクセルを描画しますcreate_rectangle。すべてのコードはGitHubにあります。実行すると、私の顔が画面に表示されます。
結論
私の顔を見せるためには、6,000語以上の説明を書かなければならないと誰が思ったでしょう。いくつかのアルゴリズムの作者がどれほど賢かったかは驚くべきことです!あなたが記事を楽しんだことを望みます。このデコーダーを書いている間、私は多くを学びました。単純なJPEG画像のエンコードにそれほど多くの計算が必要だとは思いませんでした。次回は、PNG(または別の形式)用のデコーダーを作成してみることができます。
追加資料
詳細に興味がある場合は、私が記事を書いたときに使用した資料と、いくつかの追加の作業を読んでください。