数学の観点から音楽とは何ですか? 「la」または「mi」とは何ですか?音がどのように正確に形成されるかは、ギターでよく理解されています。
サウンド「mi」(1弦のフリーサウンド)、サウンド「la」(5フレットでクランプされた1弦)。 「La」は440Hzです。 440 Hzとはどういう意味ですか?これは、ストリングが1秒間に振動する440倍です。 「mi」の音は「la」の音よりも5セミトーン低くなります(5フレットでクランプされます)。

さらに7セミトーン低くなると、再び「mi」が表示されます。オクターブ。最初の弦の自由な音と12番目のフレットでクランプされた弦の音の両方が同じ単語「mi」と呼ばれるのはなぜですか?

同じ音が鳴っているように思えます。事実、この時点までの弦の長さ(12フレットの「mi」)は正確に半分に分割されます。
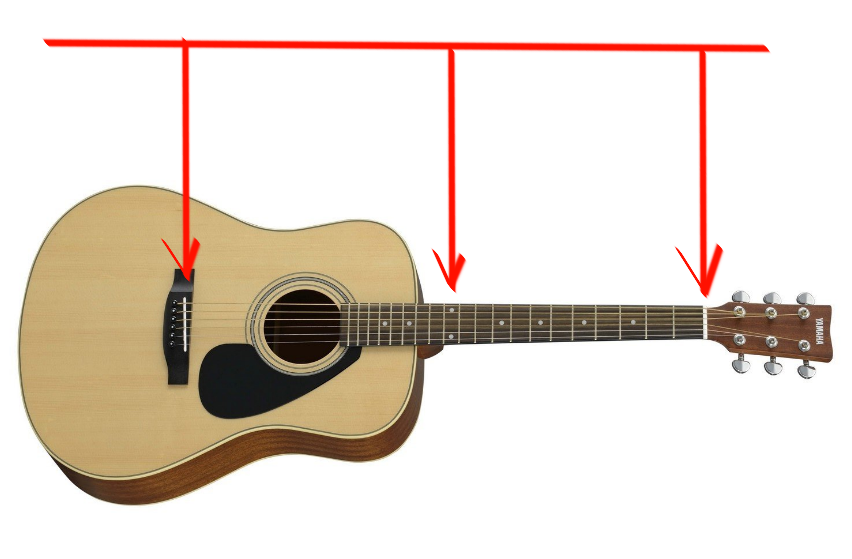
これは、物理法則によれば、弦のこの残りの部分の振動は、完全な弦の振動の2倍の頻度になることを意味します。ミュージシャンが言う
ように、弦を降りて次のフレット(フレットボードの垂直線で示される分割)でクランプするたびに、音は1セミトーン上がります。
フレットボードのフレットの幅が異なることに注意してください。周波数を1セミトーン上げるには、弦の長さを一定回数減らす必要があるため、徐々に細くなっていきます。
「オン」の何かが「イン」の何かに変換されるという事実に焦点を当てることによって、私は何を示唆していますか?数学者は、+がx(乗算)に移動する関数は(特定の条件下で)1つだけであると言うでしょう。そして、この関数は対数と呼ばれます。
これは、弦を短くして音を一定回数上げる耳は、1つのセミトーンを上げるように知覚されることを意味します。つまり、各フレットは同じ回数だけ弦を短くし、耳は1セミトーン上がって、音符「E」に到達し、オクターブを受け取ると言います。私たちの聴覚器官は対数です。
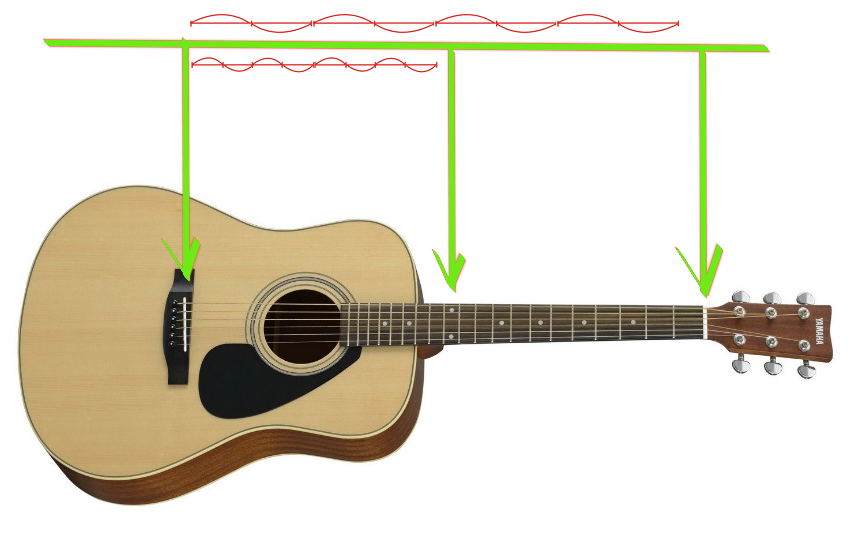
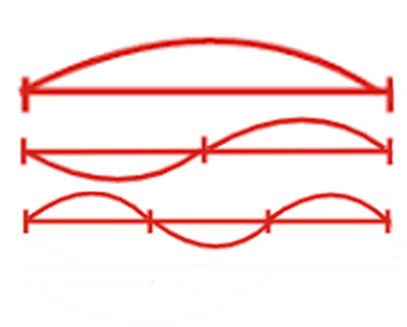
「mi」と「mi」は2倍違うと言いますが、これは音からも明らかです。上の弧はフルスイングです。真ん中にクランプすると、真ん中のグラフのように弦が振動し始めます。
なぜ音が似ているのですか?実際、弦の主な振動とともに、同じ弦の振動がすべての周波数で発生し、振動セクションの長さは周波数に反比例します。
したがって、長さを整数倍にすると、対応する倍音が聞こえます。対応する倍音は、指定された文字列によって実現されます。与えられた弦がこれらの2点で部分的に固定されて振動する場合(下のグラフ)、その音色は3倍高くなります。
周波数の2倍の増加は、同じ音として耳に知覚されます。数回分割するすべての倍音、つまりハーフセグメントの分割は、自動分割とラージセグメントの両方です。そして、大きなセグメントの一部の分割だけが、半分の分割スキームに適合しません。
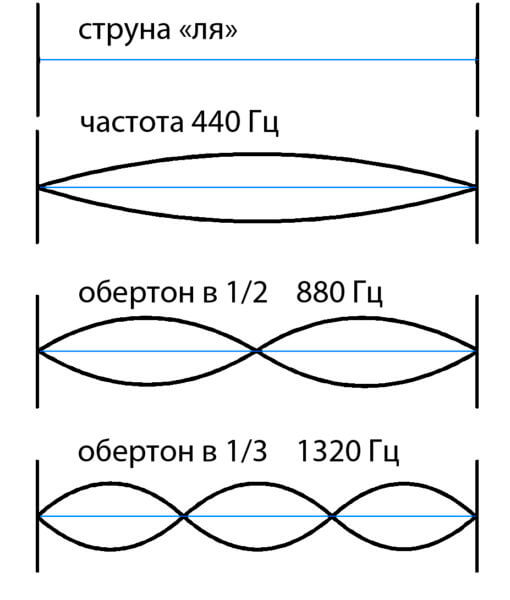
長い弦の場合は偶数の上の音をとると、半分短くなった弦の場合は上の音になります。そして、絶対に短い弦の短くなった音は長いものに聞こえます。したがって、私たちはこれらの点で私たちが聞くすべてが一致していると感じ、それを1つの音として認識します。
いくつかのセミトーンを経る音符があり、それらが私たちの耳を切るのではなく、調和、和音、耳に心地よいものとして知覚されることはさらに興味深いことです。これらのメモは何ですか?
7セミトーンを取る場合は、音符「A」を取り、次の「E」まで音を7セミトーン上げます。そうすると、これら2つの音符は良好に聞こえます。
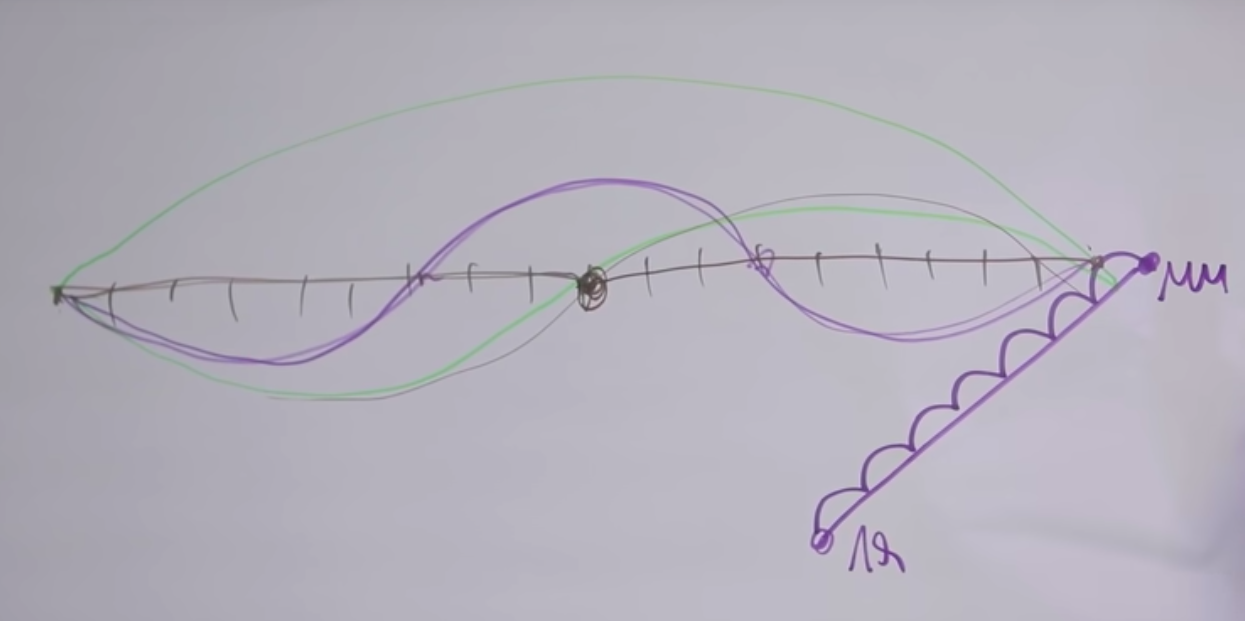
さらに5セミトーン戻ると、次のオクターブの「la」が高くなります。どういうわけか、この間隔も私たちにとって心地よいように聞こえます。それをすべて理解しましょう。
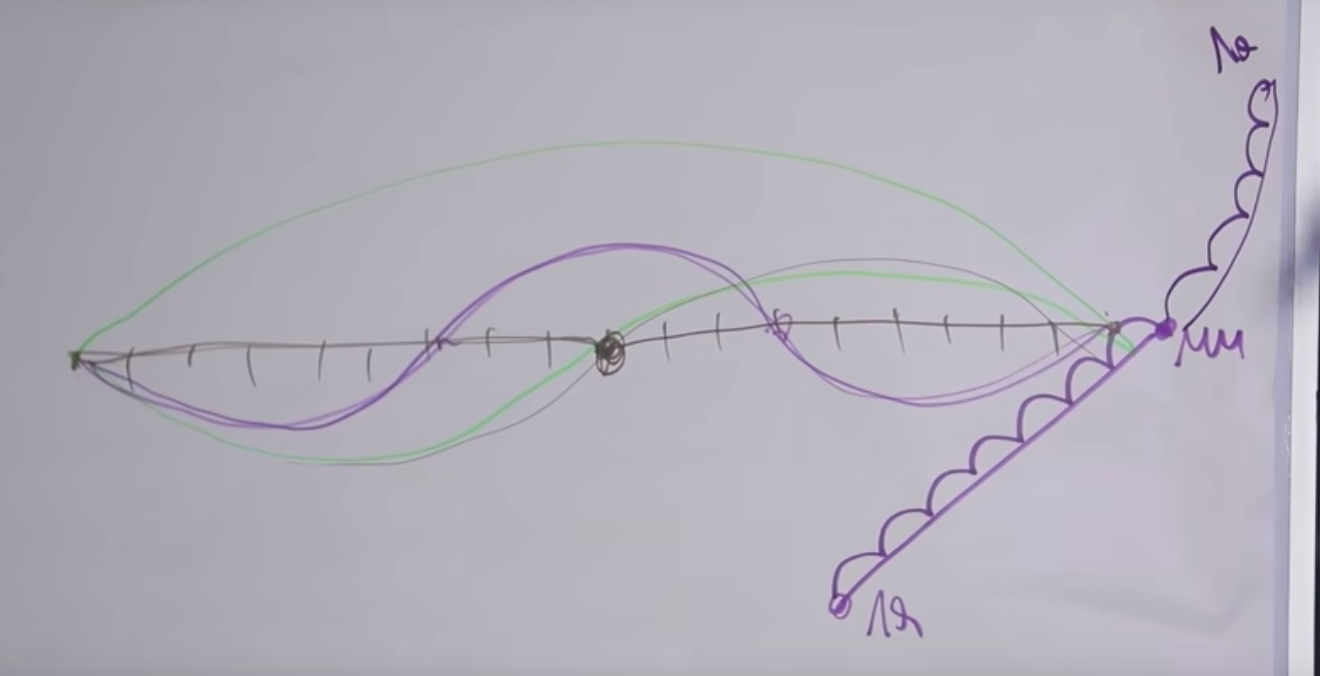
まず、1セミトーンの増加が振動の周波数の特定の回数の増加である場合、それをxと指定します。あなたが1つのより半音を調達する必要がある場合は、すでにX * Xがあるだろう、それは、xは2。私がそれを12セミトーン(x 12)上げた場合、それはちょうど2倍上げられるはずです。私たちは、方程式は、X得る12 = 2。
したがって、1セミトーンの増加は、x = 12でのストリングの収縮を意味します。音の周波数を上げ、同じである√2、または、12 √2。
そして、「la」と「mi」はそれと何の関係があるのでしょうか?7つのセミトーンがメロディックに聞こえるのはなぜですか?学位を上げましょう:
この数でとても楽しい、良いものは何ですか?
古くから、音楽の正確な録音である焼き戻しクラビエが発明されました。あなたはそれをギターで非常によく見ることができます、あなたはそれをピアノでも見つけることができます、それは中に隠されています、あなたが見るならば、あなたはひもを見ることができます。
現在、この数値は3/2に非常に近いです。計算機で計算すると、非常に正確になります。これは、「mi」が前の「la」の約1.5倍であることを意味します。それら。7トーンを上げることは、3/2倍上がることと同じです。つまり、多くの高音が一致しているということです。
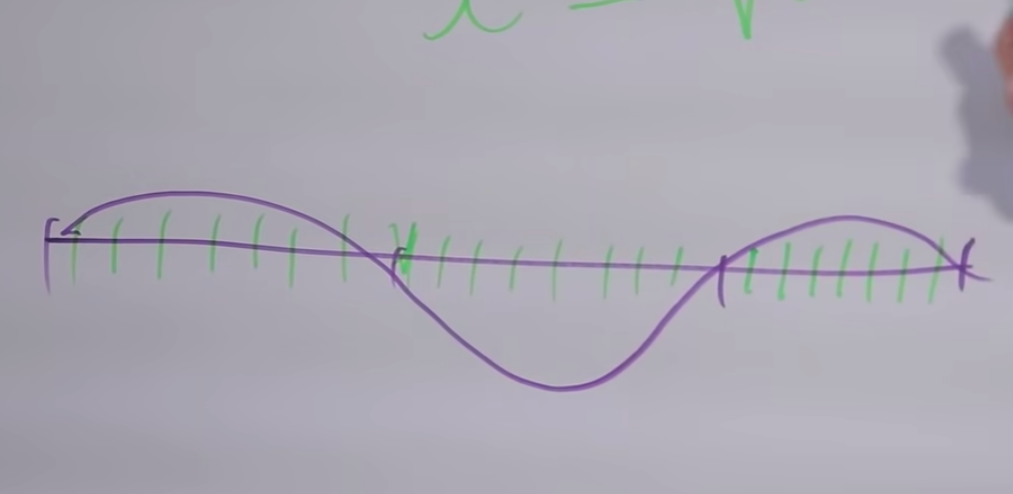
小さなセグメントの整数による除算は、セグメント全体の整数除算になるためです。そして、それに応じて、元のカットを3の倍数のピース数で割ると、小さなセグメント(1/3)と2/3の分割になります。長さから2/3を残したとき、つまり周波数を3/2に上げ、約7セミトーン上げました。多くの共通の倍音があり、心地よい調和になります。
残りの4/3は、残りの5つのセミトーン、3/2 x 4/3 = 2、ちょうど1オクターブです。これは式x71243に対応します。値は4/3に非常に近いですが、100%ではありません。この数は不合理であり、分数として書くことはできず、整数を整数で割ったものとして書くこともできません。
インドに楽器があると聞きました(シタール)、オクターブは19の部分に分割されます。セミトーン= 1/19オクターブ、19x2です。

そして、すでに非常に正確なx121932があります。つまり、このようなインドの楽器で19セグメントのうち12セグメントを後退させると、この調和でより多くの一致する倍音が発生し、この間隔は耳の香油のように聞こえます。
音楽と数学について言うべき興味深いことがたくさんあります。特に、最初の音符に4つのセミトーンが追加され、次に3つのセミトーンが追加された場合、メジャーコードが認識されます。 0-4-3。最初に3を追加し、次に4を追加した場合、マイナー。 0 --3 --4。コードの3つの音符の最初と最後は「同じ」で、7セミトーンだけ異なりますが、中間の音は私たちの調和の知覚を生み出し、マイナーモードまたはメジャーモードでチューニングします。
音楽と数学、何が共通しているのでしょうか?そして、数学者とミュージシャンはしばしばコミュニケーションをとるほど多くの共通点があり、さらに、数学者はミュージシャンを簡単に理解し、いわばセミトーンを把握します。
いくつかの便利なリンク: