🤗 🥉 📌 二次円曲線 🎴 🕛 🤴🏾

ご存知のように、ベジエ曲線は円弧や楕円を作成することはできません。この記事では、この欠点がない曲線について説明します。

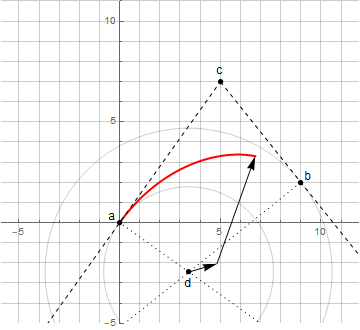
ベジエ曲線

Bezier曲線の作成の背後にあるロジックは、次のアニメーションからよく理解されています。

グラフィカル表現から直接式を取得するには、2点間の線形補間の補助関数を定義するだけで十分です。パラメーターtが0から1に変わると、aからbの中間値が返されます。

m i x (a, b, t) = a (1 - t) + b t

注意

- lerp, blend, mix - . .

その助けを借りて、あなたは一貫して必要なポイントを見つけることができます-最初に見つける

a c = m i x (a, c, t)

そして

c b = m i x (с, b, t)

そしてそれらを通して見つける

d = m i x (a c, c b, t)

必要に応じて、関数を相互に置き換えて縮小することができます。これにより計算が特に単純化されるわけではありませんが、曲線を任意の数の制御点に一般化できます（バーンスタイン多項式を使用）。私たちの場合、

d = a (1 - t)^{2} + b t^{2} + 2 c t (1 - t)

曲線の次数を増やすことは簡単に達成されます-ソースポイントは一定に設定されませんが、n +1の他のコントロールポイント間の補間の結果として：

注意

, . .

円形曲線

円弧

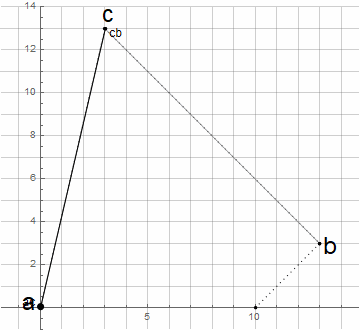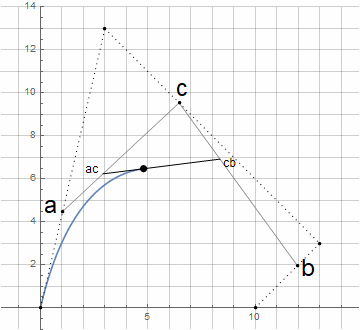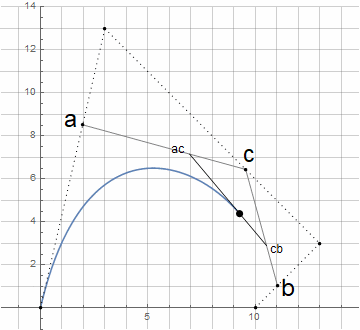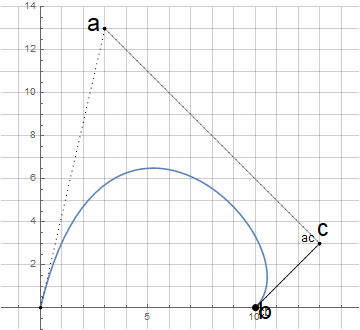
同様の方法で円弧を作成するには、コンパスで円を描くのと同様に、適切な構築ロジックを決定する必要があります。

最初は、円dの中心はわかりません。これは、点aとb（以下ノード）での接線の垂線の交点から見つかります。接線自体は、点c（以下ガイドラインと呼びます）を使用して指定されます。任意の円弧（180°未満）を作成するには、方向点から節点までの距離が同じであるだけで十分です。

楕円弧

楕円弧を作成することはすでにより困難です-異なる方向に回転する2つのベクトルが必要です（詳細はこちら）

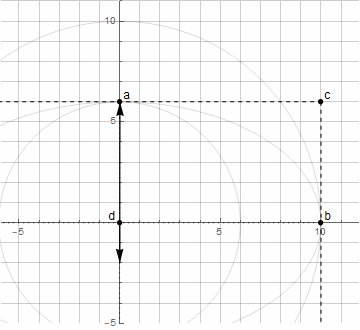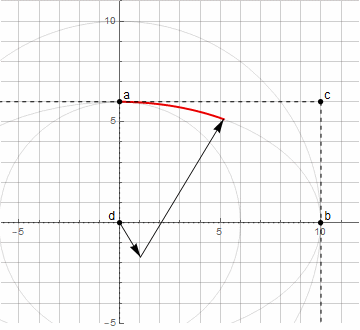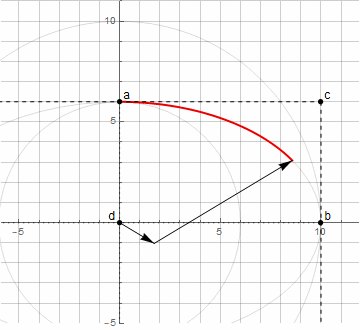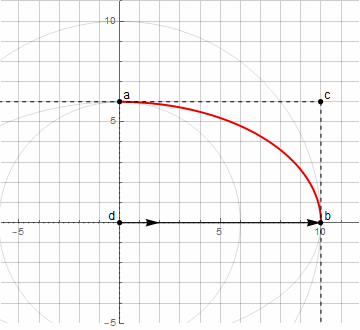
上記の点dを見つける方法を使用すると、楕円の任意の円弧を作成することはできなくなります。0°から90°まで（特定の角度で回転することを含む）のみです。

アークハイポトロコイド

描画の最初と最後でベクトルが1つの直線上になければならないという条件を設定すると、他のすべての場合にハイポトロコイドの弧が得られます。この状態は偶発的なものではなく、（曲線の一意の定義に加えて）節点での接線の一致を保証します。結果として、両方のベクトルが移動する角度パスは異なりますが、合計で180°になります。

次のアニメーションで、ガイドポイントの位置に応じて曲線の形状がどのように変化するかを確認できます。

アルゴリズム

ここでは2次元平面上で回転しているので、これらの曲線を作成する数学を複素数で説明すると便利です。

1）方向点から節点に引かれた接線の法線の交点を見つけます。

d = \frac{(2 a - c) (c - b) a^{*} + (2 b - c) (a - c) b^{*} - c (a - b) c^{*}}{(c - b) a^{*} + (a - c) b^{*} - (a - b) c^{*}}

（ここで、アスタリスクは複雑な結合を意味します）。

2）dを知ると、法線の長さがわかります

r_{ad} = | a - d |

r_{bd} = | b - d |

そしてそれらの合計と差

r_{m} = \frac{1}{2} (r_{ad} + r_{bd})

r_{s} = \frac{1}{2} (r_{ad} - r_{bd})

3）構築が始まる単位ベクトルを見つける

v = \frac{a - d}{| a - d |}

注意

sign(x).

4）各ベクトルが通過しなければならない角度パスを見つけます

ϕ_{m} = \arg (\frac{a - d}{b - d})

ϕ_{s} = \arg (- \frac{a - d}{b - d})

注意

, — . — , . . .

, — , - ; .

. ,

\arg (a - d) - \arg (b - d)

— - .

5）tを0から1に少しずつ変化させながら、次の式で曲線に属する点を求めます。

d + v (r_{m} e^{- i t ϕ_{m}} + r_{s} e^{- i t ϕ_{s}})

円形スプライン

ベジエ曲線と同様に、これらの曲線を組み合わせて、ピースごとの連続したスプラインを作成できます。アンカーポイント（ドッキング）の滑らかさを確保するには、アンカーポイントが2つの隣接する方向ポイントと一致している必要があります。これを行うには、アンカーポイントを明示的にではなく、方向ポイントの補間によって指定できます。また、完全に自動的に計算して、まったく指定することもできません。たとえば、ガイドポイント間の平均として

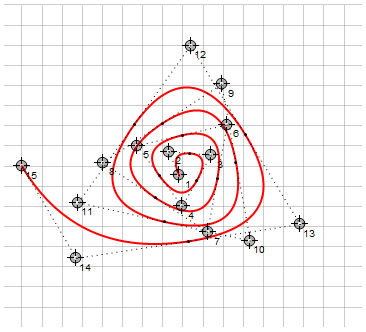
、右側では、比較のために、同じアプローチを2次ベジエ曲線で使用しました。

ノートとニュアンス

Bezier曲線とは異なり、ここでは、曲線は必ずしも制御点を結ぶ線の形状内にあるとは限りません。たとえば、

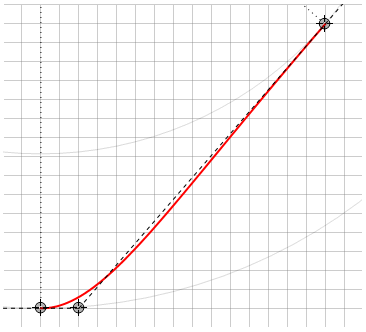
さらに、方向ポイントがアンカーポイントと同じ線上にある場合、個別に処理する必要がある縮退したケースがあります。この場合、曲線は直線に縮退し、点dを計算しようとすると、ゼロによる除算が発生します。

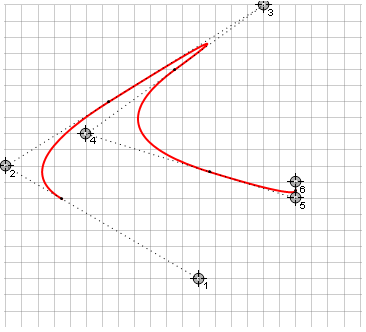
これらの曲線には、線の曲率にも制限があります。これは、アルゴリズムがたどる最小のパスを選択し、曲線が180°を超えて周回できないためです。これにより、ピースワイズ連続補間を使用すると、方向ポイントの特定の位置（右側-ベジエの同じポイント）で鋭いコーナーが発生する可能性があるという事実につながります。

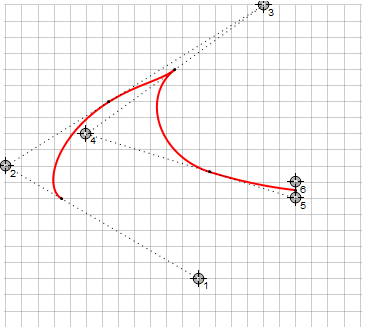
結論

カーブを構築するための考慮された方法のさらなる開発は、カーブの構築に関与するベクトルの数の増加であり、したがって、方向点の数の増加である。ただし、ベジエ曲線とは異なり、ここで次数を増やすことは明らかではなく、個別の思慮深い反射が必要です。それらをベジエ曲線と組み合わせるさまざまな方法も可能です。特に、描画ベクトルの円の中心の補間です。

考慮されている曲線の作成方法も1つだけではありません。その特定のケースは、円弧と楕円です。少なくとも、平行四辺形の直線の交点から楕円を作成できます。（ただし、このバージョンでは、作成者は失敗しました）。記事で説明されているオプションを含む他の解決策がある可能性があります-このトピックについて何か知っている場合はコメントに書き込んでください。

記事のソースコードはGitHubからダウンロードできます。

二次円曲線