🤧 👩‍🎤 🦃 オプション：プットコールホバー、ブラウニアンムーブ。オタクのための教育プログラム、パート7 🐙 🚃 ◽️

これは、オプションに関するストーリーの2番目の部分です。ここでは、プットコールの急上昇、市場の仲裁がない状態に対処し、ヘッジと複製のアイデアに精通し、ブラウンの動きとは何か、そしてそれが金融資産のレートの振る舞いのモデル化にどのように関連しているかについて話します。

詳細をよりよく理解するために少し数学があります。

この投稿は、Finmath for Fintechコースの一環として作成された、私のビデオ講義「プットコールホバーとアービトラージがないための条件」、「ブラウンモーション」のトランスクリプトです。

プットコールホバー。仲裁なし条件を使用して商品ポートフォリオの価格を分析する例

したがって、前の部分から、有効期限のプットアンドコールオプションの支払いがどのように見えるか（オプションによって提供される権利を行使できる瞬間）がわかりますが、他の期間のオプションを計算する方法も知りたいと思います。これを行うには、より複雑な数学的装置を使用して数学的モデルを構築する必要があります。ただし、その前に、put-to-callパリティ関係を見てみましょう。これは複雑ではなく、実際には非常に便利です。

ヨーロッパのオプションは、契約の購入者が、契約の将来の特定の時点で、事前に決定された価格で基礎となる資産を売買する権利を受け取るが、義務ではない契約であることを思い出してください。

基礎となる資産は、株式または通貨レートにすることができます。基礎となる資産の市場レートはスポットと呼ばれ、式では、その時点でのスポットの価値

t

$t$ として示される

S_{t}

$S_t$ ..。

基礎となる資産を購入する権利を与えるオプションは、コールオプションと呼ばれます。販売する権利はプットオプションです。オプションが将来取引を締結する権利を与える価格はストライキと呼ばれ、

K

$K$ ..。

オプションを使用できる契約で事前に合意された時間は、オプションの有効期限（有効期限）です-

T

$T$ ..。満了時の基礎となる資産レートの値は、

S_{T}

$S_T$ ..。

有効期限の支払いスケジュールを作成しましょう。特定の基礎となる資産があります-その有効期限：

S_{T}

$S_T$ 支払いだけでなく

P

$P$ 受け取ります。支払いスケジュールはこれらの調整になります

S_{T}, P

$S_T, P$ ..。設定しましょう

K

$K$ -軸のストライクレベル

S_{T}

$S_T$ ..。

最初に描画するオプションは、呼び出しオプションです。通話オプションを購入しました。

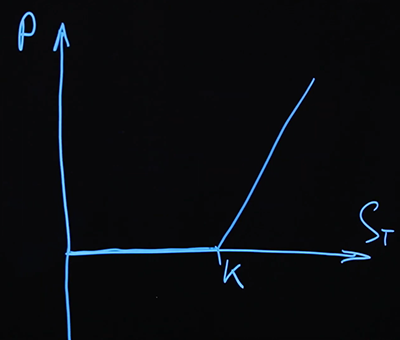
これは「ロング」コールオプションとも呼ばれ、そのオプションのプラス記号の位置です。しかし、オプションを販売することもできます。これはショートと呼ばれます。

私たちが描く2番目のオプションはショートプットです。

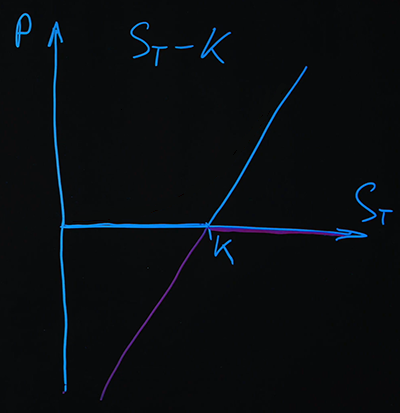
グラフでは、2つの支払いを追加すると、次のように定義される単純な線形関数が得られたことがわかります。

S_{T} - K

$S_T-K$ ）。同じ結果を分析的に得ることができます。プラス記号の付いたコールオプションの位置とマイナス記号の付いたプットオプションがあります。

C - P

$C-P$

すでに知っている分析式を使用してみましょう。

m a x (0, S_{T} - K) - m a x (0, K - S_{T})

$max(0, S_T-K)-max(0, K-S_T)$ ..。

括弧を拡張するには、2つの別々のケースを考慮する必要があります。

S_{T} > K

$S_T>K$ そして

S_{T} < K

$S_T<K$ ..。

次のシステムがあります。

{\begin{cases} S_{T} - K - 0, S_{T} > K \\ 0 - K + S_{T}, S_{T} \leq K \end{cases}

$\begin{cases} S_T-K-0, S_T>K \\ 0-K+S_T, S_T≤K \end{cases}$

どちらの場合も、同じ単純な式が得られます。

S_{T} - K

$S_T-K$ ..。

したがって、支払いは、満了時に実現された基礎となる資産の価格に関係なく、いずれの場合も同じ式で記述されます。繰り返しになりますが、私たちが引き出した支払いは、有効期限が切れた時点でのオプションの支払い（したがってコスト）であることを思い出してください。他の時点でのオプション価格の場合、それらは他のより複雑な関数によって記述されます。とりあえず条件付きで描きます。

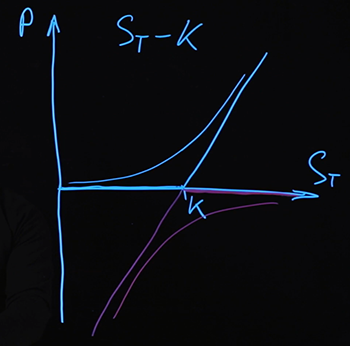
有効期限が切れる時点でのこの組み合わせの場合、支払いは次の式で決定されます。

S_{T} - K

$S_T-K$ 、任意の値

S_{T}

$S_T$ ..。有効期限時に同じ支払いを行う他の楽器の組み合わせを見つけた場合、そのような楽器の組み合わせと組み合わせのコストは言うことができます

C - P

$C-P$ 同じである必要があります。

そうでない場合は、今日、これらの楽器の組み合わせのうち、より安価なものを購入し、より高価なものを販売することで、利益を上げることができます。また、これら2つの組み合わせは有効期限で同じ支払いを行い、反対の符号でそれらを取得したため、合計支払いはゼロであることが保証されます。単に市場の商品の価格の不均衡のためにリスクなしで保証された収入を与えるそのような取引は、仲裁と呼ばれます。..。楽器の価格を計算するための数学的理論には、通常、市場に仲裁がないという仮定が含まれています。この仮定は現実と十分に一致しています。市場での仲裁の機会が発生したとしても、長くは続かない。それらを見つけて使用するのは簡単ではありません。したがって、通常、この仮定はうまく機能します。

市場に仲裁がないという条件から、

C - P

$C-P$ いつでも

t \leq T

$t≤T$ （だけでなく

T

$T$ ）機器の任意の組み合わせと同じコストで、その時点での支払い

T

$T$ 等しくなります

S_{T} - K

$S_T-K$ ..。この組み合わせは、基礎となる資産を購入することで簡単に作成できます

S

$S$ 満了時に以下の金額を返還する必要があるような金額の借金

K

$K$ ..。金融商品を扱う場合、そのような負債は、支払いを行うゼロクーポン債（債券）を販売することに相当します

K

$K$ 現時点では

T

$T$ ..。このシリーズの以前の投稿で債券と利息の詳細を読むことができます（お金の価値、利息の種類、割引と先物レート。オタクのための教育プログラム、パート1と債券：クーポンとゼロクーポン、利回り計算。オタクのための教育プログラム、パート2） ..。

したがって、コールオプションからのポートフォリオとプットオプションからのポートフォリオは、基礎となる資産のロングとショートボンドの組み合わせに等しく、有効期限ごとに1回の支払いが行われます。

K

$K$ ..。

C_{t} - P_{t} = S_{t} - B_{T} K

$C_t-P_t=S_t-B_TK$

この比率は、基礎となる資産レートに対して構築できるモデルとは無関係です。それは私たちがどのように割引を検討するかにさえ依存しません、そしてこれは市場に仲裁がないことに起因します。1つのポートフォリオをまとめ、考えられるすべてのオプションを考慮し、有効期限が切れるまでの費用を検討しました。将来のすべてのオプションで、まったく同じ費用がかかることがわかりました。したがって、別のポートフォリオの有効期限の支払いがまったく同じである場合、それらの価格は同じである必要があります。

したがって、コールオプションとプットオプションのポートフォリオの比率を取得しました。ポートフォリオを作成し、有効期限が切れたときにどのような支払いが行われるかを調べたところ、支払いは1つの線形方程式で記述されていることがわかりました。コールオプションとプットオプションの支払い機能とは異なり、それぞれに2つのセクションがあります。

S_{T}

$S_T$ ..。これにより、どのような状況でも満了時に同じ支払いを行う、よりシンプルな商品のポートフォリオを構築できます。これら2つのポートフォリオの価格は、有効期限が切れたときだけでなく、いつでも同じになります。これは、市場に仲裁がないという条件によって保証されています。市場に仲裁があり、この平等が満たされない場合、それに応じて、これらのポートフォリオの1つを購入し、別のポートフォリオを販売して、保証された勝利を得ることができます。この比率は、たとえば、基礎となる資産の価格について構築できる数学モデルには依存しません。この比率は、どのモデルでも満たす必要があります。

この比率もこのように見ることができます。同じリスクを持ついくつかの資産のポートフォリオをまとめました。公式は、一方では基礎となる資産に関連するリスクを伴う資産を収集するように書き直すことができます。つまり、これらの機器に固有のすべてのリスクを排除できます。そのようなパッケージがどれだけの価値があるかを正確に知っている、基礎となる資産の将来の価格に関連する不確実性。

C_{t} - P_{t} - S_{t} = - B_{t} K

$C_t-P_t-S_t=-B_tK$

リスクを取り除くこの方法は、ヘッジと呼ばれます。私たちは、同じリスクのいくつかが埋め込まれているいくつかの手段のポートフォリオを構成しますが、これらのリスクが相互にバランスを取り、それを取り除くような比率でそれらを選択します。このアイデアは、他のより複雑なヘッジ戦略で使用されます。検討中のケースは非常に単純であり、特定のオプションの組み合わせでのみ作業できます。

このアイデアを反対側から見ると、これらのツールの1つを他のツールで表現できます。たとえば、市場に1つ、プットオプションがある場合、自動的にコールオプションを受け取ります。この場合、それは複製になります-ある製品の支払いを他の製品を通じて複製しました。ヘッジと複製は、数学的には互いに密接に関連しており、非常によく似た計算です。

この場合、非常に単純な状況であり、リスクを完全にヘッジするか、支払いを複製するために、ポートフォリオを1回作成するだけで済み、有効期限が切れるまで待って、支払いはすでに保証されています。これは静的レプリケーション（静的ヘッジ）と呼ばれます）。これはまれなケースであり、通常は機能しません。この効果をより一般的に達成するためには、動的なヘッジ戦略に頼る必要があります。つまり、一度ポートフォリオを作成しますが、満了時の支払いが希望どおりになるように、常に何かを追加したり、変更したりする必要があります。

これは、プットコールの急上昇の興味深い比率です。計算が非常に単純であるという事実にもかかわらず、彼の例では、より複雑なケースに適用されるいくつかの非常に重要なアイデアを見ることができます-仲裁なしの条件の適用、支払いの複製、リスクのヘッジ。ここで、この単純な関係を終了し、より複雑なモデルの構築に進むことができます。

コールオプションとプットオプションの比率だけでなく、市場で観察された値の関数としてのオプション価格も提供するモデルを構築したいと思います。これには、より複雑な数学的理論が必要になります。

ブラウン運動とは何ですか、そしてロバート・ブラウンは誰ですか。コンピューターでブラウンの動きをシミュレートする方法。幾何学的なブラウン運動とは

私たちがこれまで考えてきたことは、非常に単純な数学的装置、実際には学校の数学でうまくいくことを可能にしました。先に進んでより複雑な数学モデルを構築するには、これだけでは不十分であり、「大人の」数学の要素が必要です。したがって、さらなるプレゼンテーションへの一般的なアプローチは次のようになります。単純なケースで数学装置がどのように機能するかを明確にする実例を示し、使用する定式化と定理も示します。私はこれらの定理を証明しません。数学の部分に興味がある人は、対応する教科書やビデオコースを参照することができます。

私たちが必要とする最初の概念はブラウン運動です..。この用語が物理学で何を意味するかを覚えておきましょう。これは、このプロセスが正式な数学モデルでどのように配置されるかを示す一種の明確な例になります。

多くの人が「ブラウンモーション」という言葉を使っていると思います学校の物理学カリキュラムに関連付けられています。多くの人が、この概念を科学的流通に導入したのはブラウンという名前の物理学者であり、彼の姓から判断すると、英国人であると信じています。興味深いことに、これらの仮定はすべて間違っています。まず、この科学者の名前はロバートブラウンでした。これは、ロシア語では「ロバートブラウン」と読む必要があります。これは18〜19世紀の教育を受けた人にとっては明らかではないかもしれませんが、その最初の外国語はフランス語で、2番目はドイツ語でした。第二に、彼はイギリス人ではありませんでした-彼はスコットランド人でした、それは私たちが理解しているように、まったく同じことではありません。しかし、最も興味深いのは、彼が物理学者ではなく、植物学者だったことです。彼が彼の有名な実験を行って説明したとき、彼は顕微鏡下で花粉粒子を研究していました。スライド上の標本は、一滴の液体の形で準備され、その中に花粉粒子が置かれ、花粉がすべてのドラフトから飛び散らないようにし、静かに見ることができます。

ブラウンの注意は、彼が顕微鏡のアイピースで見るものが静止画ではないという事実に引き付けられました。彼は、比較的言えば、混沌とした動きをする丸い粒子を観察しました。今日、この現象には簡単な説明があることがわかっています。この粒子の周りの溶液には多くの分子があり、それらは非常に頻繁にランダムな方向に相互作用し、その結果、粒子はある種の複雑な動きをします。

その動きを描くと、ランダムな軌跡になります。

これは私たちの主題分野と何の関係がありますか？実際、類推は簡単です。時間の経過に伴う金融資産の割合を考慮します。多くのランダムな要因が、その粒子だけでなく、あらゆる瞬間に作用します。ロバート・ブラウンが顕微鏡を通して個々の分子を見なかったように、私たちはそれらを見ません。

これらのランダムな要因の累積的な影響は、資産の過程の変化につながります-分子の累積的な影響が花粉粒子の変位につながるのと同じように。これらのプロセスは時間内に継続的に発生します。したがって、金融資産のレートが実現されます。コースの時間依存性はランダムに得られるため、このような軌跡はブラウンモーションと呼ばれます。私たちの場合、ランダムな偏差は1つの軸の周りでのみ発生するため、これは1次元のブラウン運動です。

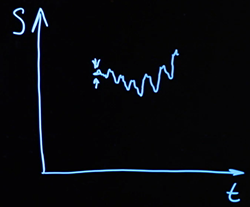
私たちが使用するプロセスの正式な数学的モデルは、別の科学者、アメリカの数学者NorbertWienerの名前に関連付けられています。こんな感じです。連続時間関数を検討しています。なぜなら

t

$t$ が連続している場合、関数

W (t)

$W(t)$ 継続的。

これにはランダムなコンポーネントが含まれており、数学的に次のように決定されます。

△ W_{△ t}

$\triangle W_{\triangle t}$ -時間増分が交差しない場合は独立。

時点からの関数の増分

t

$t$ その瞬間まで

t + s

$t+s$ 通常、パラメータ0および

s

$s$ （時間間隔の長さ）。

W_{t + s} - W_{t} \sim N (0, s)

$W_{t+s}-W_t∼N(0,s)$

以下では、コンピュータ上でそのようなパスを生成できることが非常に重要であることがわかります。これは、多くの計算方法で必要です。どうすればこれを行うことができますか？時間は理論的な数学モデルでは連続的であり、コンピューター上でいくつかの増分に分割します。通常は固定ステップです。プロセスが開始する特定の開始点を座標で作成します

W_{0}; t_{0}

$W_0;t_0$ ..。次に、後続のタイムステップごとに、そのような分布を持つランダム変数を生成し、それを1ステップ移動します。私たちはあらゆる点でこれを行います。結果は破線です。

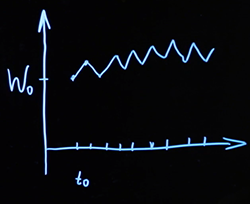
どこかで増分がプラス記号で、どこかでマイナス記号で判明しました。その結果、特定の各ポイントで、プロセス全体の値は、これらすべてのランダム変数の累積合計によって決定されます。単位時間あたりの平均変位をスケーリングできるようにするために、通常は文字で示される追加のパラメーターを導入することもできます。

σ

$\sigma$ （正規分布に関して）。機能を考えることができます

σ W_{t}

$\sigma W_t$ どこ

W_{t}

$W_t$ 標準的なブラウン運動であり、

W_{t}

$W_t$ 必要なものに応じて、変動が広くなるか狭くなります。

このようなプロセスが整ったら、オプションの価格を計算するのに役立つ数学モデルを構築したいと思います。連続時間での割引に関心を持って行ったのと同じ原理に従って方程式を作成しましょう。これはある種の微分方程式になります。

一定額の利息計算の問題を解決していたとしたら

P

$P$ 連続時間では、小さな時間ステップで正しい関係が得られます

△ P = r P △ t

$\triangle P=rP\triangle t$ または

\frac{△ P}{P} = r △ t

$\frac{\triangle P}{P}=r\triangle t$ 、

ここで

r

$r$ リスク中立の金利です。そして限界に行く

Δ t \to d_{t}

$Δt →d_t$ 、微分方程式を取得します

\frac{d P}{P} = r d t

$\frac{dP}{P}=rdt$ ..。

それから、継続的な時間で割引するためのすでにおなじみの式を取得します

P = P_{0} e^{r t}

$P=P_0e^{rt}$ どこ

P_{0}

$P_0$ 初期値です。

この推論の論理を、将来の価格がランダムな要因に依存する資産の数学モデルに適合させたいと思います。私たちの資産の価格の相対的な変化は、リスク中立率の類似物である特定のパラメーターによって特徴付けられます（この場合、パラメーターは私たちの基礎となる資産を特徴づけ、リスク中立率ではありません）。この式に、ブラウン運動によって記述される確率的要素を追加しましょう。

\frac{Δ S}{S} = μ Δ t + σ Δ W

$\frac{ΔS}{S}=μΔt+σΔW$

実際に結果が出ました。限界に移動して、連続時間割引で簡単に解いた式と非常によく似た式を取得しましょう。

\frac{d S}{S} = μ d t + σ d W

$\frac{dS}{S}=μdt+σdW$

しかし、技術的な問題があります。重要なのは、ブラウン運動（ウィーナープロセス）は、私たちが定義したように、時間の連続関数ですが、古典的な数学的分析の意味では区別できないということです。これは正式に証明できます（証明は省略します）。

このようなモデルを数学的に厳密に構築するには、式にどのような意味を入れるかを決定する必要があります。

d W

$dW$ ..。このためには、確率的微分を使用する必要があります。その名前は、別の数学者の名前である伊藤微分に関連付けられています。これは、従来の計算で使用されているルールとは異なるルールに従います。

参考までに、この数学的装置に関して必要な結果を書きます。伊藤ディファレンシャルはこれらのルールに従います。

場合

d x = a (x, t) d t + b (x, t) d W_{t}

$dx=a(x,t)dt+b(x,t)dW_t$ 、

その後

f (x, t)

$f(x,t)$ ：

d f = \frac{\partial f}{\partial t} d t + \frac{\partial f}{\partial x} d x + \frac{1}{2} \frac{\partial^{2} f}{\partial x^{2}} d x^{2}

$df=\frac{∂f}{∂t}dt+\frac{∂f}{∂x}dx+\frac{1}{2}\frac{∂^2f}{∂x^2}dx^2$ ..。

この規則は、従来の計算で2つの変数の関数を区別する方法とは異なります。2つの独立した変数がある場合、通常の計算では、部分的な導関数を取り、展開の最初の2つの項で停止します。伊藤式の関数の微分の展開の3番目の要素は、通常の関数ではなく、ランダムで確率的なプロセスで作業しているために正確に表示されます。この結果は、証明することなく、既成のものと見なします。

言うべきことがもっとあります

d x^{2}

$dx^2$ 最後の式で。条件別

d x = a (x, t) d t + b (x, t) d W_{t}

$dx=a(x,t)dt+b(x,t)dW_t$ 、それを二乗すると、要因を持つ用語があります

d t d W_{t}

$dt dW_t$ 、

d t^{2}

$dt^2$ 、

d W_{t}^{2}

$dW^2_t$ ..。伊藤式を適用するには、次のことを行う必要があります。

d t d W_{t} = 0

$dt dW_t=0$ ;

d t^{2} = 0

$dt^2=0$ ;

d W_{t}^{2} = d t

$dW^2_t=dt$ ..。

伊藤積分が何であるかを理解すれば、これらの規則はすべて自然になりますが、私たちの目的では、伊藤式を正しく適用する方法を知っていれば十分です。

そして今、私たちはオブジェクトを操作する方法を知っているので、技術的な複雑さを克服することができます

σ d W

$σdW$ ..。

変数として

x

$x$ 基礎となる資産レートがあります

S

$S$ 、私たちはそれを表現することができます：

d S = S μ d t + σ S d W_{t}

$dS=Sμdt+σSdW_t$ ..。

次に、関数の微分を書く方法を知っています。

S

$S$ そして

t

$t$ ..。関数の微分は何であるか見てみましょう

f (S, t) = l n (S)

$f(S, t)=ln⁡(S)$ ..。

d l n S = d f = \frac{\partial f}{\partial t} d t + \frac{\partial f}{\partial S} d S + \frac{1}{2} \frac{d^{2} f}{d S^{2}} d S^{2} =

$dln S = df = \frac{∂f}{∂t}dt+\frac{∂f}{∂S}dS+\frac{1}{2}\frac{d^2f}{dS^2}dS^2=$

= 0 d t + \frac{1}{S} (S μ d t + σ S d W_{t}) - \frac{1}{2} \frac{1}{S^{2}} σ^{2} S^{2} d t

$=0 dt+\frac{1}{S}(Sμdt+σSdW_t)-\frac{1}{2}\frac{1}{S^2}\sigma^2 S^2 dt$

ここで、用語を収集すると、対数の式が得られます。

S

$S$ ..。

d ㏑ S = (μ - \frac{σ^{2}}{2}) d t + σ d W

$d㏑S=(μ-\frac{\sigma^2}{2})dt+σdW$

今、私たちは何が等しいかを知っています

㏑ S

$㏑S$ （通常の分布であることに注意してください）。の表現に直接興味があります

S

$S$ ..。

S = S_{0} e^{μ t} e x p (σ W_{t} - \frac{σ^{2}}{2} t)

$S=S_0 e^{μt}exp(σW_t-\frac{\sigma^2}{2}t)$

上記の式は、幾何学的なブラウン運動を表しています。これは、パラメータを使用して指数関数的な成長を表します

μ

$\mu$ 最初はポイントから始まります

S_{0}

$S_0$ 、および式に従って、この指数の周りにノイズが重ね合わされます

e x p (σ W_{t} - \frac{σ^{2}}{2} t)

$exp(\sigma W_t-\frac{\sigma^2}{2}t)$ ..。これはすでにコンピューターで読み取ることができ、ブラウン運動のパスを生成できます。基礎となる資産レートのパスのいくつかの可能な実現を取得します。この式には2つのパラメーターがあります。

σ

$\sigma$ -分散と

μ

$\mu$ -ドリフト。それらは、正規分布の分散と正規分布のバイアスに対応します。

㏑ S

$㏑S$ ..。私が言ったように、今ではコンピューターでシミュレートすることが可能ですが、このプロセスを使用してオプションの価格を計算できるようにするために導入する必要があるもう1つの理論的コンポーネントがあります。次に、リスク中立対策について説明します。

このシリーズのすべての記事

オプション：プットコールホバー、ブラウニアンムーブ。オタクのための教育プログラム、パート7

プットコールホバー。仲裁なし条件を使用して商品ポートフォリオの価格を分析する例

ブラウン運動とは何ですか、そしてロバート・ブラウンは誰ですか。コンピューターでブラウンの動きをシミュレートする方法。幾何学的なブラウン運動とは

More articles: