記事を理解するには、学校の数学コースで十分です。
シュヴァルツシルト計量の因子の形は、その絶妙な重複で長い間私を悩ませてきました、そして私はそれを変換する方法を見つけることに時間を割くことに決めました。シュヴァルツシルトメトリック自体は、真空の場合の一般的な相対性を解いた結果として取得されます(エネルギー-運動量テンソルはゼロです)。
これは、任意のコンパクトで巨大なオブジェクトの近くにある時空間の連続体を表します。コンパクト。これは、形状の偏差が質量に対して重要でないことを意味します。簡単に言えば、丸くてきつい。通常、ここでは例としてブラックホールが使用されます。何らかの理由で、コンパクトでないオブジェクトの例を示す人は誰もいません。非コンパクトオブジェクトなどの巨大なオブジェクトから無限の距離にあるオープンスペースの気密フォームスティック。遠くにある立方体の馬から、彼の目にも悲しみが見えます。
3球のボリュームを通して
交換します:
次に、メトリックは次のようになります。
式のすべての数値が重要であるため、交換は光の速度の4度に注意を引くためにのみ必要でした。これは、物理学の歴史全体によって証明されています-時間の経過とともに経験的に得られた式は、それに含まれるすべての数学形式の意味を説明する理論的基礎を受け取ります。
通常、このメトリックの表現では、物理定数に関連付けられた部分とフィールドを作成する体の質量は、シュヴァルツシルト半径で表されます。
この時点でメトリックに特異性があるためです。ここで、時間は文字通り止まります。
メトリック全体は次のようになります。
しかし、現象の物理的本質についての推論の続きで、この2つ:
また、理解する必要があります。したがって、次のように表します。
重力半径の半分です 、およびその寸法は同じです。我々が得る:
それはそれ自体を示唆しています:
すでに悪くはない。描きましょう。想像してみてください エンドセグメント、 -下の図に示すように、その一部。それは明らかです..。

ちなみに、どれが不思議です その結果、ポイント エネルギーオブジェクトのイベントホライズンの後ろ(下)にあります ..。見つけるのはとても簡単ですが、見つけることはできません。
ここで、フォームの関係を示します に垂直に幾何学的な場所を持つすべてのポイントに対して実行されます その時点で :
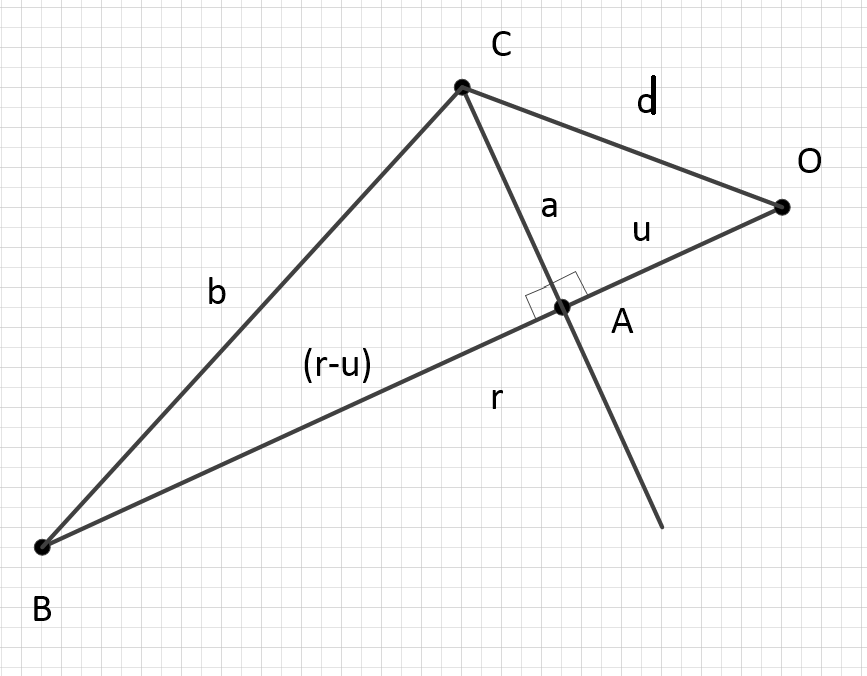
のために そして ..。
簡単に言えば、正方形の違い に投影される量の差に相当します です そして それぞれ、ポイントが それらには共通点があります。
さらに、 そして 逆に、予測 一部の軸、つまり、元の形式で互いに垂直な2つの量のピタゴリアンの合計。これを要件に変換し、ケースを検討しますそれが真実である:

確定します 最初の反復と同様:
これが4度です。3球の体積の公式:
つまり、乗算と除算を行うと オン :
次に、シュヴァルツシルトメトリックの係数は、フィールドの中心を基準にしたポイントの2つの放射状投影の周りに構築された2つの3球の体積の差になり、ポイントとフィールドの中心の間の合計距離によって形成される3球の体積と相関します。
全半径が投影によって与えられるという事実を考慮に入れると、この構造全体は2つのパラメーターによって非常に簡潔に設定されます。1つはエネルギーに関連し、もう1つはそうではありません。正確に2つの座標があります。
結論
このような表現の注目すべき結果は次のとおり
です。1。乗数の形式から、光子の動作が5次元時空間の可視ゾーンを制限していることがわかります。それの外では、あなたは重力のあるものを隠すことができますが、見えません。
2. 2番目の隠れた座標の存在は、ゼロ時間のパラドックスを排除します。
3.巨大な物体の周りの空間の曲率は、常に2つの成分に分解できます。一方は物体のエネルギーに関連付けられ、もう一方は空間のみに関連付けられます。次のステップは、5次元時空間の真空の場合の一般的な相対性の方程式を解くことです。これについては次の記事で詳しく説明します。
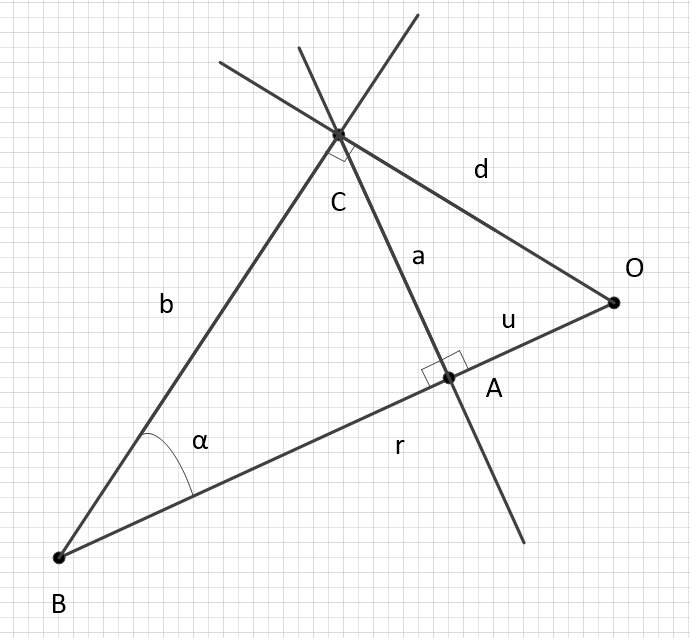
ボーナス。角を曲がった
明らかに、平坦な角度を通る点での磁場の重要性を表すことができます。これは、平坦な空間からの運動の軌道の偏差を表します(重力場がない場合)。
量を表現しましょう そして 角を曲がった : ..。それを軌道の曲がり角と呼びましょう。次に、係数は非常に異なる方法で表すことができます。
私は特にタンジェントバージョンが好きです。
元の間隔で置き換えます:
当然のことながら、すべてがフラットなミンコウスキーメトリックになります。 ..。
間違いなく5番目があるはずです...
続く。