🗜️ 🤪 👩🏿‍🤝‍👩🏾 極座標で星（およびそれ以上）を描く方法 💔 🤧 🌱

極座標のポリゴンの公式の問題は、主題のリソースで定期的に発生します-そして、明確な答えがないまま定期的に残ります。最良の場合、分割の残りの部分の関数を介して解決策に出くわします。これは、関数に対して分析変換を実行できないため、数学的な観点からは「クリーン」ではありません。どうやら、本当の数学者は千年紀の問題を解決するのに忙しくて、そのような平凡な問題に注意を払うにはフェルマットの定理の簡単な証拠を探しています。幸いなことに、この問題では、想像力が知識よりも重要であり、この問題を解決するには、トポロジー科学の教授である必要はありません。学校レベルの知識で十分です。

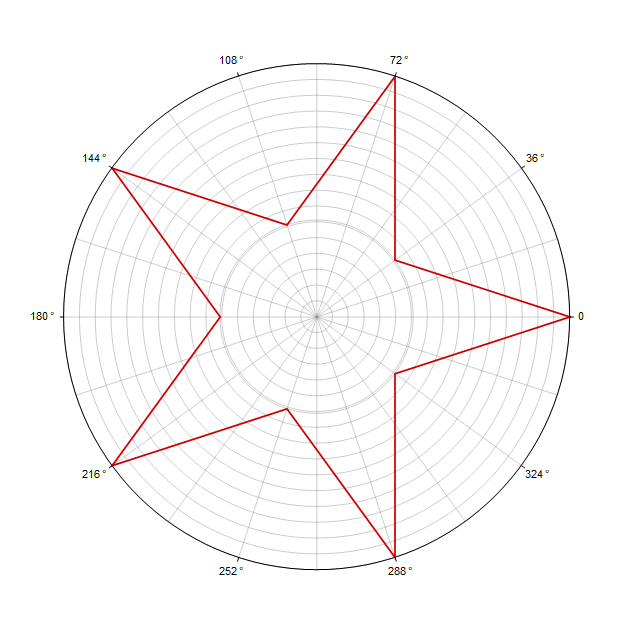
極座標での等辺ポリゴンの式は非常に単純に見えます

ρ = \frac{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k \cos (n ϕ)) + π m}{2 n})}

$\rho = \frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k \cos (n \phi ))+\pi m}{2 n}\right)}$

次のパラメータがあります。

ϕ

$\phi$ -角度;

n

$n$ -凸状の頂点の数。

m

$m$ -側面が1つの直線上にある頂点の数を決定します。負の値も許容されます-記号は星が曲がる方向を決定します;

k

$k$ -剛性-で

k = 0

$k=0$ 他のパラメータに関係なく、円を取得します。

k = 1

$k=1$ -からの中間値での直線を持つポリゴン

0

$0$ 前

1

$1$ -円とポリゴンの中間の図形。

この式を使用すると、2つの方法で星を描くことができます：

1）

n = 5, m = 3

$n=5, m=3$

2）

n = 5 / 4, m = 0

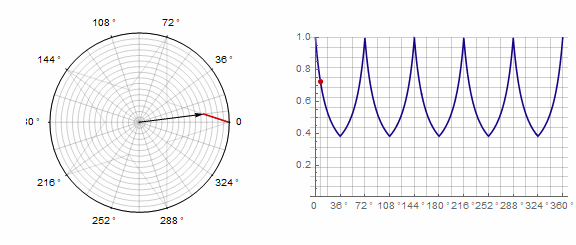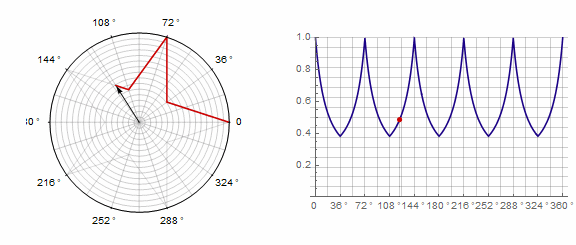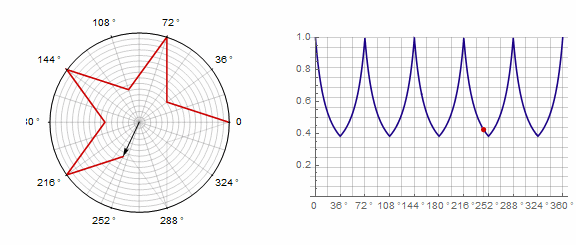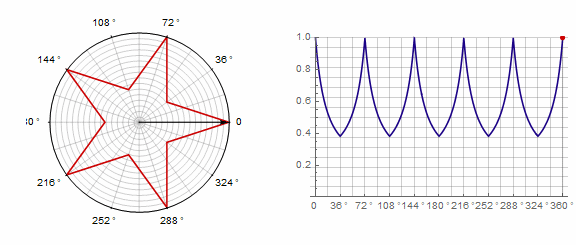
$n=5/4,m=0$ ..。この場合、1ターンではなく2ターンする必要があります。

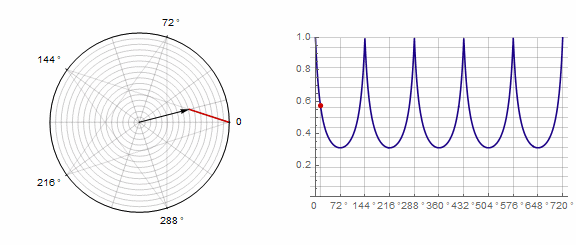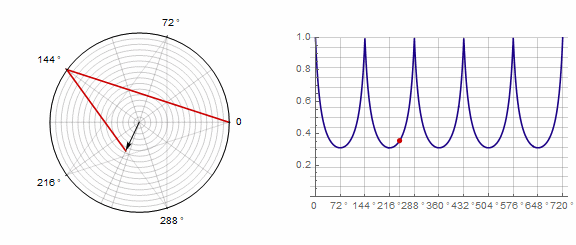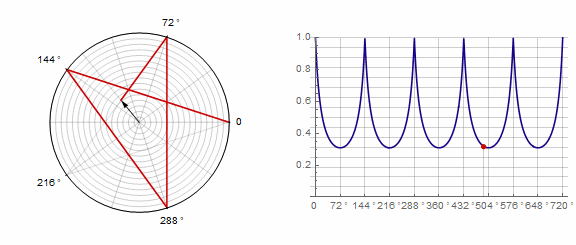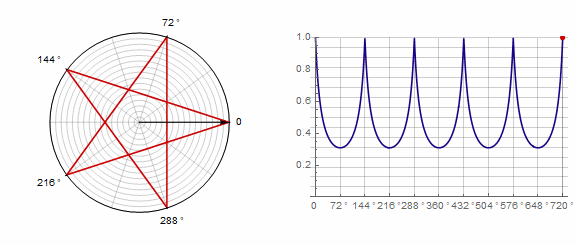
パラメータ

m

$m$ ポリゴンに次のように影響します（ここでは-1から5に変更されます）。

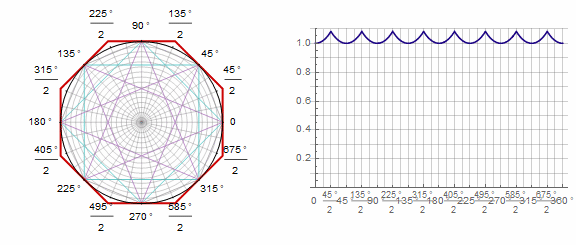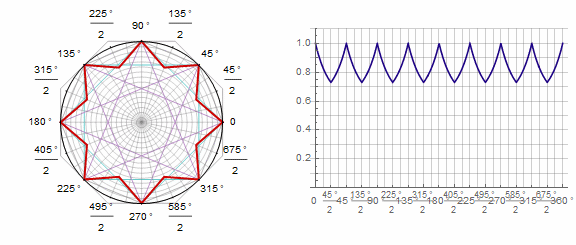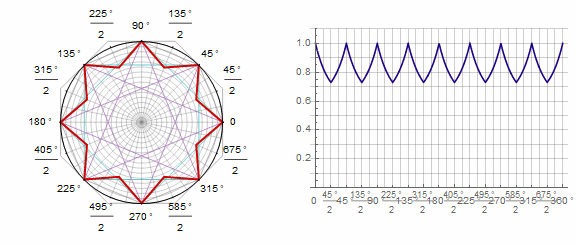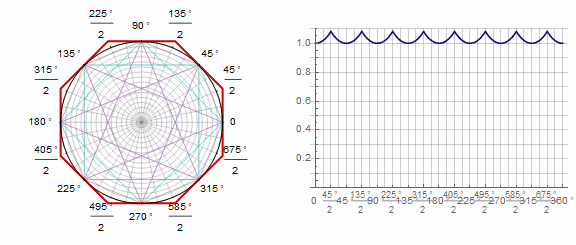
パラメータ

k

$k$ アニメーションで：

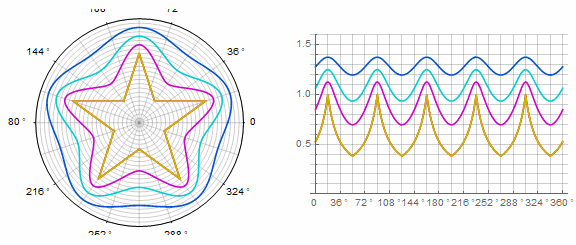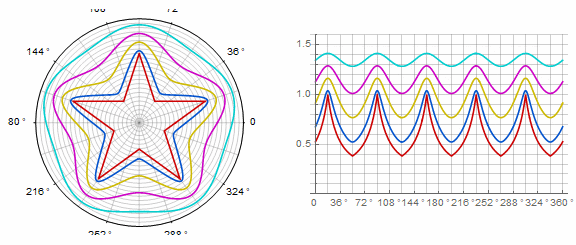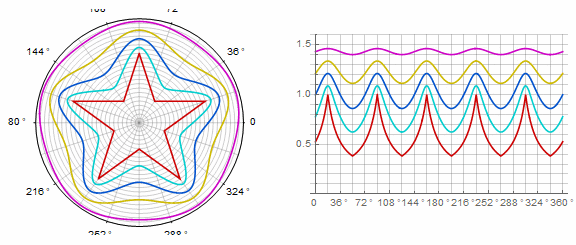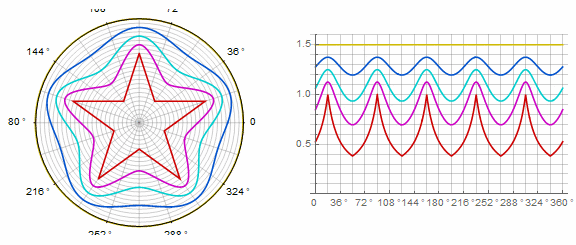
複雑なフォームと変更

元の式を複雑な形式で書き直すことができます。仮想単位が含まれていても、半径の値は引き続き有効です。

ρ = \frac{4^{1 / n} {(\sqrt{1 - k^{2}} + i k)}^{- 1 / n} (1 + {(\sqrt{1 - k^{2}} + i k)}^{2 / n} e^{\frac{i π m}{n}}) {(\sqrt{1 - k^{2} \cos^{2} (n ϕ)} + i k \cos (n ϕ))}^{1 / n}}{4^{1 / n} + e^{\frac{i π m}{n}} {(2 \sqrt{1 - k^{2} \cos^{2} (n ϕ)} + 2 i k \cos (n ϕ))}^{2 / n}}

$\small\rho = \frac{4^{1/n} \left(\sqrt{1-k^2}+i k\right)^{-1/n} \left(1+\left(\sqrt{1-k^2}+i k\right)^{2/n} e^{\frac{i \pi m}{n}}\right) \left(\sqrt{1-k^2 \cos ^2(n \phi )}+i k \cos (n \phi )\right)^{1/n}}{4^{1/n}+e^{\frac{i \pi m}{n}} \left(2 \sqrt{1-k^2 \cos ^2(n \phi )}+2 i k \cos (n \phi )\right)^{2/n}}$

公式がもう少し面倒になっているので、一見、これは無意味に思えるかもしれませんが、結論にジャンプしないでください。まず、アークサインが含まれていません。これにより、式の数学的な意味が完全に変わり、星型ポリゴンの構築を別の方法で見ることができます。第二に、それはまた、例えば、特別な場合のためのコンパクトな式を得るために使用することができます

\frac{i^{t} {(i^{n t})}^{1 / n}}{1 + {(i^{n t})}^{2 / n}}

$\frac{i^t \left(i^{n t}\right)^{1/n}}{1+\left(i^{n t}\right)^{2/n}}$ ..。第三に（そして最も興味深いことに）、それは創造的に修正され、他の予期しない形を得ることができます。半径内の可能な虚数成分の出現が計算のあいまいさを引き起こさないようにするために、を掛けることによってそれをすぐにカルテシアン座標に減らすことができます。

e^{i ϕ}

$e^{i \phi }$ ..。いくつかの変更の例を次に示します。

\frac{(- 1)^{2 / 3} e^{i ϕ} {(i \cos (3 ϕ) + \sqrt{\sin^{2} (3 ϕ)})}^{1 / 3}}{(- 1)^{2 / 3} + 2^{2 / 3} {(i \cos (3 ϕ) + \sqrt{\sin^{2} (3 ϕ)})}^{2 / 3}}

$\frac{(-1)^{2/3} e^{i \phi } \left(i \cos (3 \phi )+\sqrt{\sin ^2(3 \phi )}\right)^{1/3}} {(-1)^{2/3}+2^{2/3} \left(i \cos (3 \phi )+\sqrt{\sin ^2(3 \phi )}\right)^{2/3}}$

\frac{e^{i ϕ} \sqrt{i \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)}}}{e^{i / 2} + \sqrt{2} {(i \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)})}^{3 / 2}}

$\frac{e^{i \phi } \sqrt{i \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}}}{e^{i/2}+\sqrt{2} \left(i \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}\right)^{3/2}}$

\frac{e^{\frac{1}{4} i (4 ϕ + π)}}{2 \sqrt{(- 1)^{1 / 4} \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)}} - 1 - i}

$\frac{e^{\frac{1}{4} i (4 \phi +\pi )}}{2 \sqrt{(-1)^{1/4} \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}}-1-i}$

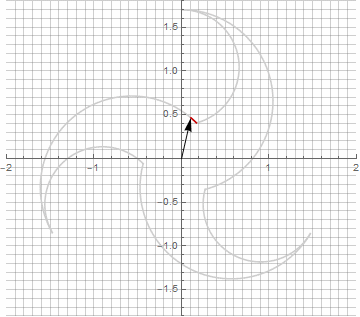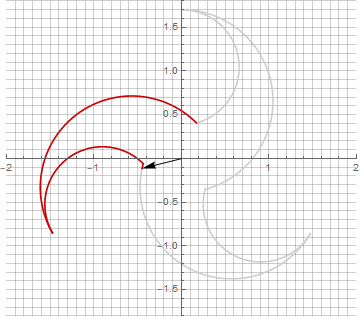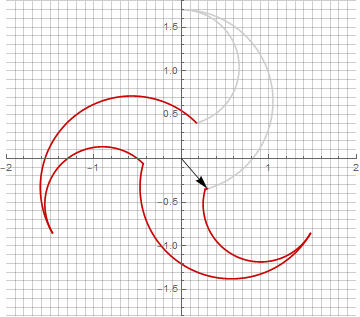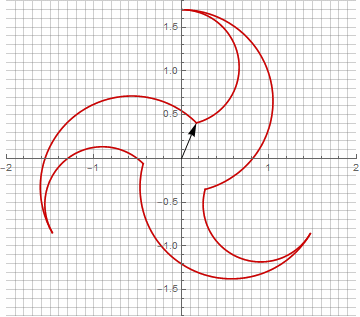
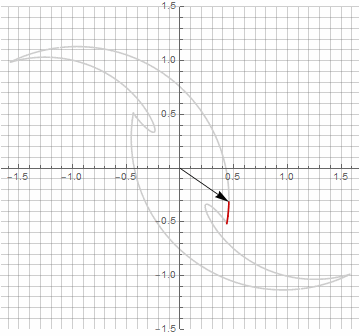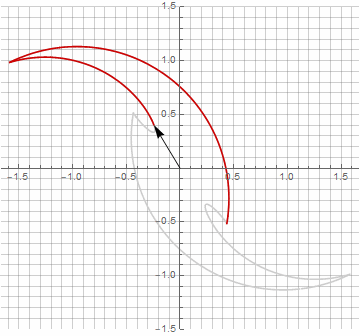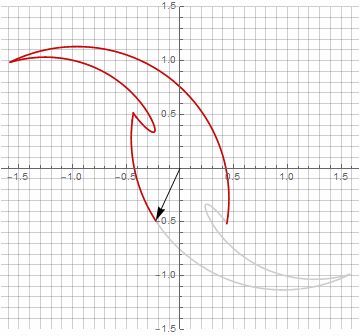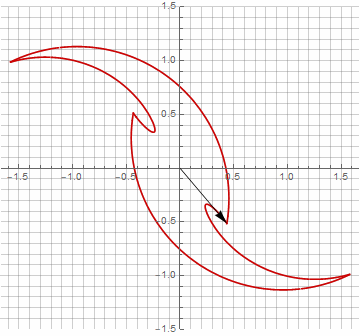
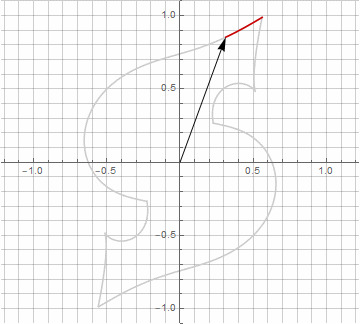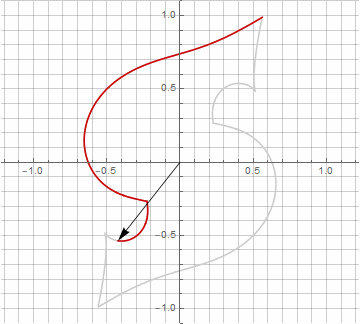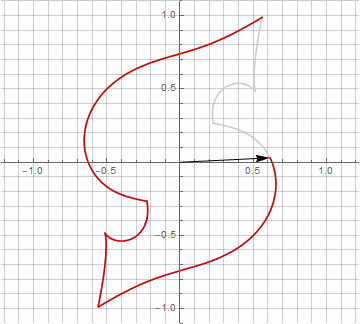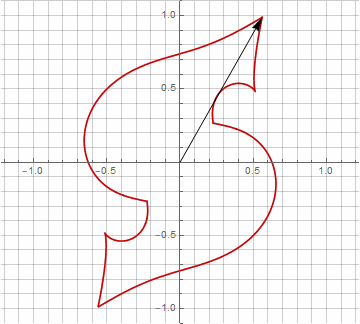
お気づきかもしれませんが、ベクトルの回転は均一ではなくなりました。これは、半径に虚数成分が出現したためです。

クワッドなど

私たちの式には素晴らしい特別なケースがあります-正方形、その式は次のように書くことができます

ρ = \frac{2}{\sqrt{2 + \sqrt{2 + 2 \cos (4 ϕ)}}}

$\rho = \frac{2}{\sqrt{2+\sqrt{2+2 \cos (4 \phi )}}}$

または

ρ = \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 ϕ)}}}

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 \phi )}}}$

（あなたが一番好きなものを選んでください）。

もう少し発展したケースでは、点を通る円と正方形の中間の図形を定義できます

(k, k)

$(k,k)$ 表面に

ρ = \sqrt{\frac{2}{1 + \sqrt{1 - \frac{(2 k^{2} - 1) \sin^{2} (2 ϕ)}{k^{4}}}}}

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\frac{\left(2 k^2-1\right) \sin ^2(2 \phi )}{k^4}}}}$

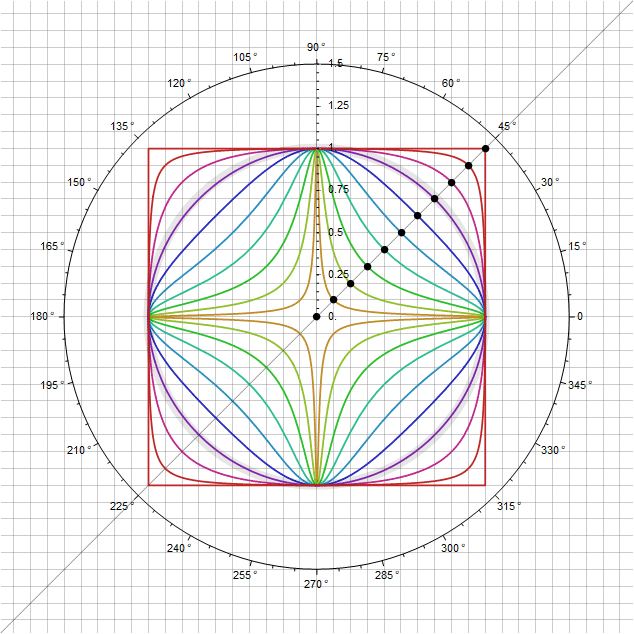
ポイントを通過する状態を維持しながら、これらの形状にバリエーションを追加することもできます

(k, k)

$(k,k)$ -パラメータ自体を直接変調する

k

$k$ 角度に応じて、対角線を通過するときにその乗数が1に等しくなります。たとえば、代わりに

k

$k$ 関数

\frac{k}{1 - z \cos^{2} (2 ϕ)}

$\frac{k}{1-z \cos ^2(2 \phi )}$ 、追加のパラメータを取得します

z

$z$ 追加の曲げを調整できます。特に、

z = 1 / 4

$z=1/4$ 次のようになります。

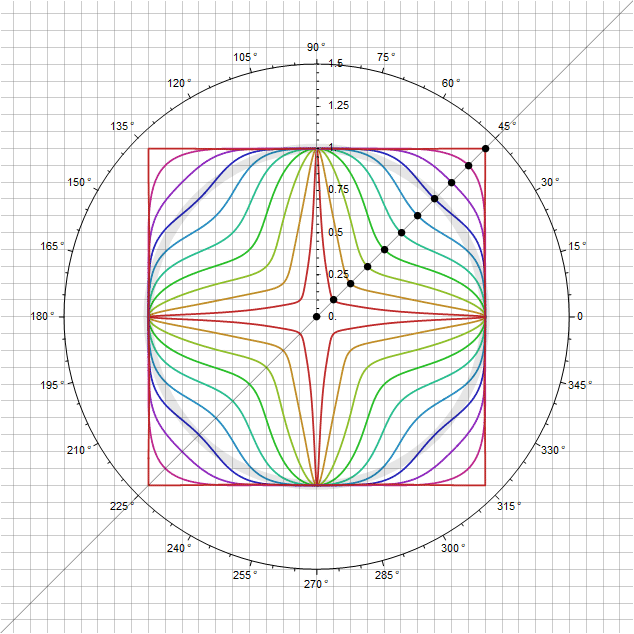
さらに拡張されたケースでは、正方形だけでなく長方形を定義しても、極座標で定義できます。

ρ = \sqrt{\frac{4 a^{2} b^{2}}{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2}) (\sqrt{1 - \frac{4 a^{2} b^{2} k \sin^{2} (2 ϕ)}{{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2})}^{2}}} + 1)}}

$\rho = \sqrt{\frac{4 a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(\sqrt{1-\frac{4 a^2 b^2 k \sin ^2(2 \phi )}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}+1\right)}}$

そして、その面積を（楕円積分を介して）計算することさえできます：

S = 4 a b \frac{(k - 1) K (k) + E (k)}{k}

$S=4 a b\frac{(k-1) K(k)+E(k)}{k}$

注意

k

$k$ (

0

$0$

1

$1$ ) ,

π a b

$\pi a b$

4 a b

$4 a b$ .

これにより、断面積が制御された円から長方形に遷移するプロファイルを作成できます。ここで、面積は一定です。

そしてここで、領域は指数関数的に拡大します。

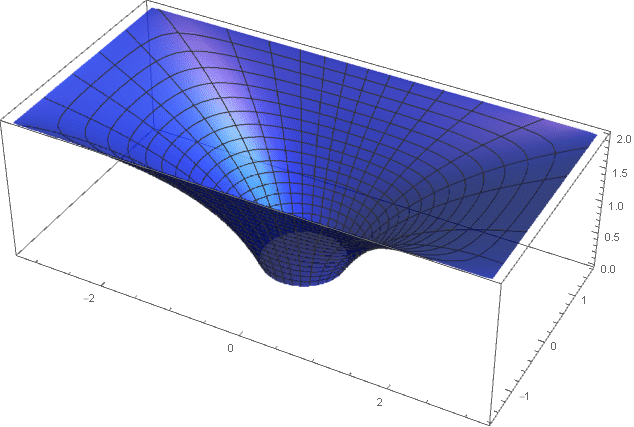
カルテシアン座標に移動

極座標の式は、カルテシアン座標の式を介して、少なくとも2つの方法で表すことができます。図の境界の勾配の形式がどのように変化するかに応じて異なります。これを行うには、座標のアークタンジェントを通る角度を計算し、減算することによって半径ベクトルを介して式を定数にするだけで十分です。

0 = \sqrt{x^{2} + y^{2}} - \frac{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k \cos (n \tan^{- 1} (x, y))) + π m}{2 n})}

$0=\sqrt{x^2+y^2}-\frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}$

または分割

1 = \frac{\sqrt{x^{2} + y^{2}} \cos (\frac{2 \sin^{- 1} (k \cos (n \tan^{- 1} (x, y))) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}

$1=\frac{\sqrt{x^2+y^2} \cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}$

2番目のオプションは、ポリゴンの側面に沿って直線のグラデーションを与えるため、推奨されます。

注意

, (0,0) - — , , (

- \cos (\frac{2 \sin^{- 1} (k) + π m}{2 n}) \sec (\frac{2 \sin^{- 1} (k \cos (\frac{π n}{2})) + π m}{2 n})

$-\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right) \sec \left(\frac{2 \sin ^{-1}\left(k \cos \left(\frac{\pi n}{2}\right)\right)+\pi m}{2 n}\right)$ ).

\cos (n \tan^{- 1} (x, y))

$\cos \left(n \tan ^{-1}(x,y)\right)$

\frac{(x + i y)^{n} + (x - i y)^{n}}{2 {(x^{2} + y^{2})}^{n / 2}}

$\frac{(x+i y)^n+(x-i y)^n}{2 \left(x^2+y^2\right)^{n/2}}$ , A034839.

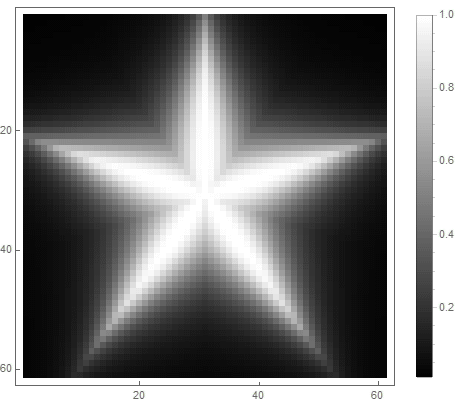
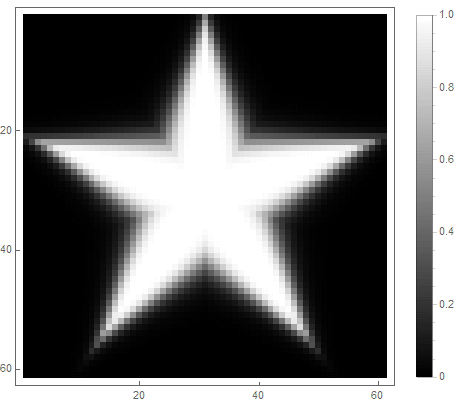
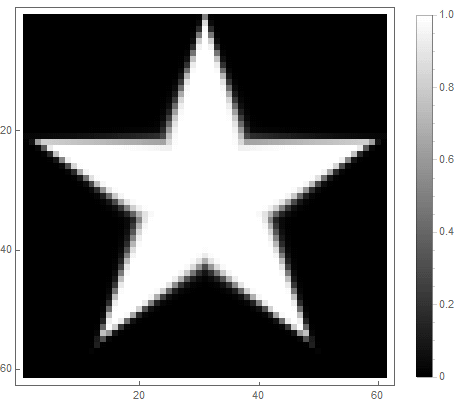
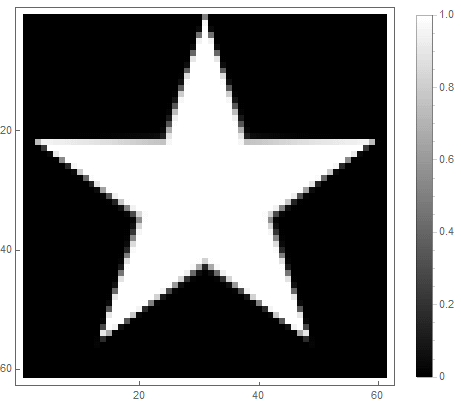
式の右辺からの式の値（2番目の場合）は、

0

$0$ 前

1

$1$ ポイントの場合

(x, y)

$(x,y)$ 図の中に入り、から

1

$1$ adinfinitum-そうでない場合。さまざまな関数を選択して明るさに変換することで、さまざまなラスター化オプションを取得できます。指数の場合（

e^{- x - 1}

$e^{-x-1}$ 最初と

e^{- x}

$e^{-x}$ 2番目のオプションの場合）

または、飽和している場合

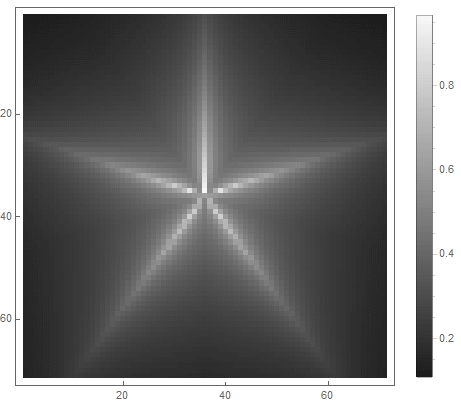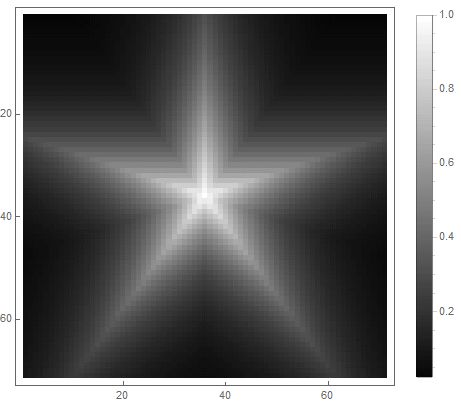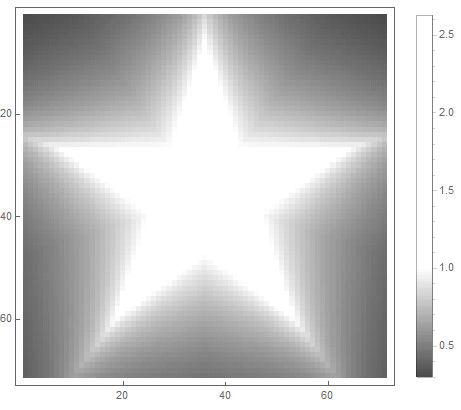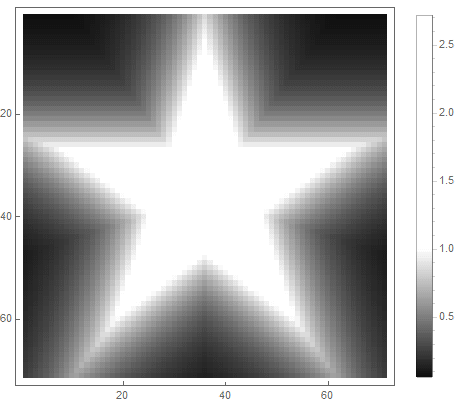クラシックなローパスフィルターを使用できます

\frac{1}{1 + x^{p}}

$\frac{1}{1+x^p}$ 、その中で

p

$p$ -減衰の程度を決定するフィルターの次数。

最初のオプションの場合：

そして2番目に：

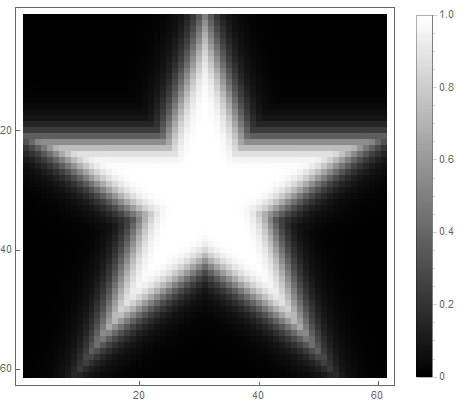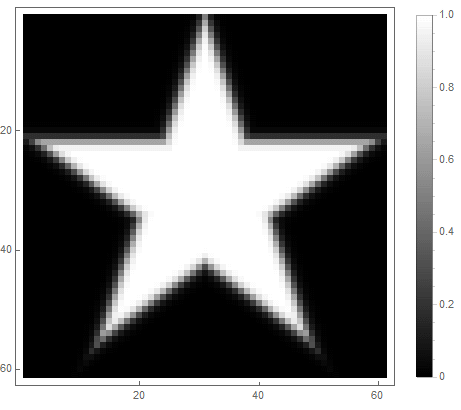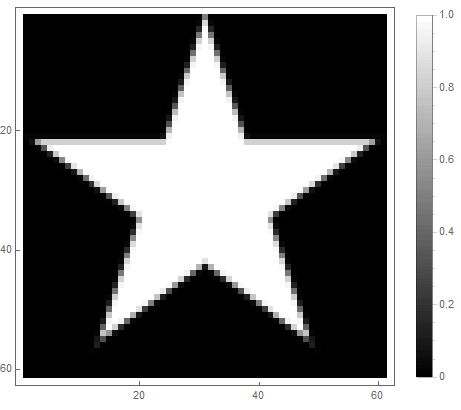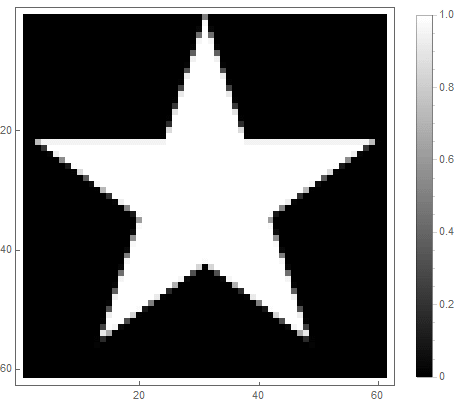補間境界を明示的に設定することにより、ピースワイズ連続関数を使用することもできます。

ラスター化自体に加えて、変形を設定することもできます。たとえば、チェッカーボードを円に押し込みます。

または、球の上に引っ張ることもできます。

式

x = \frac{u}{\sqrt{\frac{2}{1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |}}}

$x=\frac{u}{\sqrt{\frac{2}{1+ \left| \frac{u^2-v^2}{u^2+v^2} \right|}}}$

y = \frac{v}{\sqrt{1 + \frac{2}{| \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |}}}

$y=\frac{v}{\sqrt{1+\frac{2}{\left| \frac{u^2-v^2}{u^2+v^2}\right| }}}$

z = \sqrt{1 - \frac{1}{2} u^{2} (1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |) - \frac{1}{2} v^{2} (1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |)}

$z=\sqrt{1-\frac{1}{2} u^2 \left(1+\left| \frac{u^2-v^2}{u^2+v^2}\right|\right)-\frac{1}{2} v^2 \left(1+\left| \frac{u^2-v^2}{u^2+v^2}\right|\right)}$

付録：式がどのように導き出されたか

数学的なテキストでの物語の古典的なスタイルは、レンマ/定理とその証明の交代で構成されています-証明可能なステートメントが上からの啓示によって著者の頭に現れたかのように。そして、これにはいくつかの真実がありますが、多くの場合、式の出現の前にいくつかの研究が行われ、その説明は正式な証明よりもその意味をより深く理解することができます。そして、ステートメントの忠実度は、ステートメントにつながったステップの忠実度を通じて追跡できます。

したがって、ここでも-記事が複雑な形式の式で始まっている場合、その外観は自明ではなく直感に反し、宣言されたプロパティには追加の証拠が必要になります。しかし、三角測量形式の記録では、その出現の履歴を追跡することは非常に可能です。

1）最も単純なケース、つまり極座標で直線を描くタスクから始めます。これを行うには、方程式を解く必要があります

r \cos (ϕ) = 1

$r \cos (\phi )=1$ その解決策は明らかです

r \to \sec (ϕ)

$r\to \sec (\phi )$ ..。

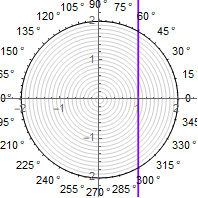
2）さらに、直線でねじれを提供するには、secant引数を「ループ」する必要があります。他のソリューションが分割残余の形で「ダーティハック」を使用するのはこの段階です。また、直接および逆正弦関数の順次取得も使用します-

\sin^{- 1} (\sin (ϕ))

$\sin ^{-1}(\sin (\phi ))$

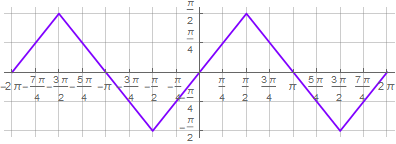
このアプローチにより、結果の式に対して標準的な数学演算を実行できます。

例えば

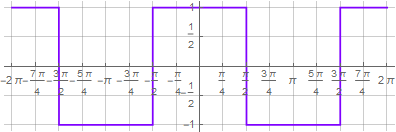
\frac{\partial \sin^{- 1} (\sin (ϕ))}{\partial ϕ} = \frac{\cos (ϕ)}{\sqrt{1 - \sin^{2} (ϕ)}}

$\frac{\partial \sin ^{-1}(\sin (\phi ))}{\partial \phi }=\frac{\cos (\phi )}{\sqrt{1-\sin ^2(\phi )}}$

同じ表記法のおかげで、三角関数の複雑な表現を使用して、極座標の二乗関数をより美的な外観に単純化することができます。Wolfram Mathematicaでは、これはTrigToExp関数とExpToTrig関数を使用して実行できます。

コード

Sec[1/2 ArcSin[k Sin[2 \[Phi]]]]^2//TrigToExp//ExpToTrig//Sqrt[#]&//FullSimplify

↓

\frac{2}{\sqrt{2 + 2 \sqrt{1 - k^{2} \sin^{2} (2 ϕ)}}}

$\frac{2}{\sqrt{2+2 \sqrt{1-k^2 \sin ^2(2 \phi )}}}$

同じ記録のおかげで、追加の乗数を使用して、円と正方形の間の滑らかな中間図を取得できます

k

$k$ そのため、アークサインの議論は1つに満たない-

\sin^{- 1} (k \sin (ϕ))

$\sin ^{-1}(k \sin (\phi ))$ ：

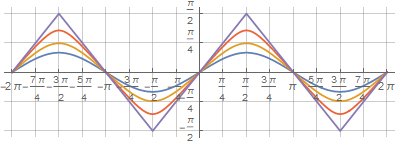
そして、関数が特定のポイントと交差するためには、方程式を作成して再計算する必要があります

k

$k$ ：

\sqrt{\frac{2}{1 + \sqrt{1 - k^{'} \sin^{2} (\frac{π}{2})}}} = k

$\sqrt{\frac{2}{1+\sqrt{1-k' \sin ^2( \frac{\pi}{2} )}}}=k$

コード

Solve[(Sqrt[2/(1+Sqrt[1-k Sin[2 \[Phi]]^2])] /. \[Phi]->Pi/4)==x, k] /. x->k

↓

k^{'} \to \frac{4 (k^{2} - 1)}{k^{4}}

$k'\to \frac{4 \left(k^2-1\right)}{k^4}$

3）パラメータ

n

$n$ そして

m

$m$ 創造的な方法で追加されたばかりで、実際、それらの効果は実験的に調査されました。

4）パラメトリックビューに移動し、軸を「ストレッチ」することで、長方形を簡単に取得できます。

x = a \cos (t) \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 t)}}}

$x=a \cos (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

y = b \sin (t) \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 t)}}}

$y=b \sin (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

しかしその後

t

$t$ 角度を意味しなくなりました

t

$t$ 座標軸への投影を通じてベクトルを記述する単なるパラメータです。極座標に戻るには、ベクトルの長さ（二乗和の根を通る）、角度（比率の逆正接を通る）を見つけ、この角度を次のように表す必要があります。

ϕ

$\phi$ 代わりに、結果の式を置き換えます

t

$t$ ..。

コード

With[{r = Sqrt[2/(1 + Sqrt[
      

        
        
        
      

    
 1 - Sin[2 t]^2])]}, {Sqrt[(a r Cos[t])^2 + (b r Sin[t])^2], 
      

        
        
        
      

    
 ArcTan[(b r Sin[t])/(a r Cos[t])]}] // Simplify

↓

{\sqrt{2} \sqrt{\frac{a^{2} \cos^{2} (t) + b^{2} \sin^{2} (t)}{\sqrt{\cos^{2} (2 t)} + 1}}, \tan^{- 1} (\frac{b \tan (t)}{a})}

$\left\{\sqrt{2} \sqrt{\frac{a^2 \cos ^2(t)+b^2 \sin ^2(t)}{\sqrt{\cos ^2(2 t)}+1}},\tan ^{-1}\left(\frac{b \tan (t)}{a}\right)\right\}$

Solve[ArcTan[(b Tan[t])/a]==\[Phi], t]

↓

t \to \tan^{- 1} (\frac{a \tan (ϕ)}{b})

$t\to \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)$

Sqrt[2] Sqrt[(a^2 Cos[t]^2 + b^2 Sin[t]^2)/(1 + Sqrt[Cos[2 t]^2])]
      

        
        
        
      

    
/. t -> ArcTan[(a Tan[\[Phi]])/b] // Simplify

↓

\sqrt{2} \sqrt{\frac{a^{2} b^{2} \sec^{2} (ϕ)}{(a^{2} \tan^{2} (ϕ) + b^{2}) (\sqrt{\cos^{2} (2 \tan^{- 1} (\frac{a \tan (ϕ)}{b}))} + 1)}}

$\sqrt{2} \sqrt{\frac{a^2 b^2 \sec ^2(\phi )}{\left(a^2 \tan ^2(\phi )+b^2\right) \left(\sqrt{\cos ^2\left(2 \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)\right)}+1\right)}}$

このような式を単純化することはすでにより困難であり、これにはいくつかの段階が必要になります。

置き換えてカルテシアン座標に移動します $\phi \to \tan ^{-1}(x,y)$ ;
指数形式に移動します。
簡素化する;
逆の交換をする $x\to \cos (\phi )$ そして $y\to \sin (\phi )$ ;
指数形式に戻ります。
簡素化する。

その結果、次の式が得られます。

コード

Sqrt[2] Sqrt[(a^2 b^2 Sec[\[Phi]]^2) /
      

        
        
        
      

    
((1 + Sqrt[Cos[2 ArcTan[(a Tan[\[Phi]])/b]]^2])
      

        
        
        
      

    
(b^2 + a^2 Tan[\[Phi]]^2))] /. \[Phi] -> ArcTan[x, y] 
      

        
        
        
      

    
// TrigToExp // Simplify 
      

        
        
        
      

    
// # /. {x -> Cos[\[Phi]], y -> Sin[\[Phi]]} & 
      

        
        
        
      

    
// TrigToExp // Simplify // FullSimplify

↓

2 \sqrt{\frac{a^{2} b^{2}}{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2}) (1 + \sqrt{\frac{{((a^{2} + b^{2}) \cos (2 ϕ) - a^{2} + b^{2})}^{2}}{{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2})}^{2}}})}}

$2 \sqrt{\frac{a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(1+\sqrt{\frac{\left(\left(a^2+b^2\right) \cos (2 \phi )-a^2+b^2\right)^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}\right)}}$

結論

ご覧のとおり、ポリゴンのような単純でありふれたものでも、何か新しいものを見つけて思いつくことができます。そして、話はそれだけではありません。一般的な場合の面積式は不明のままであり、通常のポリゴンだけでなく任意のポリゴンの式も不明のままであり、パワーおよび三角測量系列への拡張は考慮せずに残されました。3次元の場合にも同様の式が存在する可能性があります。

したがって、数学のすべてがすでに発明されており、普通の人の理解を超えた問題しかないという場合は、信じないでください。実際の数学者が気付いていない、純粋に実用的な問題がたくさんあります。または、周囲に十分な誇大宣伝がないため、または解決のためにそれらを達成する方法の大まかな考えをすでに持っているため、解決に興味がありません。ウィキペディアで解決策が入手できない問題に取り組むことを恐れないでください。解決策を公開することを恐れないでください。また、すべての役に立たないことについての記事の下にあるコメントを読むことを恐れないでください。

PSは、Mathematicaの元のドキュメントをここからダウンロードします。

極座標で星（およびそれ以上）を描く方法

複雑なフォームと変更

クワッドなど

カルテシアン座標に移動

付録：式がどのように導き出されたか

結論

More articles: