数学者は、原則としていくつかの問題を解決できないという事実に長い間慣れようとしてきました。

私たちは何でも可能だと言いたいです。ジャスターノートンの本「Cuteandthe Magic Booth」では、「不可能だと知らなければ多くのことが可能になる」という理由で、王はミロに彼の目標が達成できないことを知らせることを拒否しています。transl。]。しかし、現実の世界では、本当に不可能なことがいくつかあり、数学でそれを証明することができます。
人々は「不可能」という用語をさまざまな方法で使用します。彼は、シャッフルされたカードの2つの同一のデッキを見つけるなど、ありそうもないことを説明することができます。議会の図書館全体を手作業で書き直すなど、時間、スペース、またはリソースの不足のためにほぼ不可能なタスクを説明できます。パーペチュアルモーションマシンなどのデバイスは、その存在が私たちの物理学の理解と矛盾するため、物理的に不可能です。
数学的不可能性は異なります。明確な仮定から始め、数学的な推論と論理を使用して、いくつかの結果は不可能であると結論付けます。運、粘り強さ、時間、またはスキルの量がタスクを実行可能にすることはありません。数学の歴史は不可能の証拠でいっぱいです。これらの多くは、数学の最も注目すべき結果であると考えられています。しかし、必ずしもそうではありませんでした。
おそらく最初の不可能の証拠に対する罰は厳しかった。歴史家は紀元前5世紀にそれを信じています。メタポンのヒッパサスピタゴラスの信奉者である、は、通常の五角形の辺の長さと対角線の長さの両方を測定できる線セグメントを見つけることが不可能であることを発見しました。今日、一辺の長さが1の通常の五角形の対角線の長さは黄金の比率であり、ϕ = 1/2(1 +√5)-は不合理な数であると言います。ヒッパの発見は、「すべてが数である」というピタゴリアンの信条への挑戦でした。そのため、伝説によれば、ヒッパサスは海で溺死したか、単にピタゴリアンの仲間から追放されました。
1世紀以上後、ユークリッドは線と円を幾何学の基本曲線として高めました。その後、多くの世代の幾何学者は、コンパスと定規の助けを借りてのみ、角度の分割、垂直線の描画など、あらゆる種類のものを描画しました。しかし、単純で困惑したギリシャの幾何学模様のように見えた特定の構造は、結果として神話上の地位を獲得し、2000年以上にわたって数学者を悩ませてきました。これらは、任意の角度を3つの部分に分割し、その体積が指定されたものの2倍の体積である立方体の側面を構築し、すべての通常のポリゴンを構築し、また、与えられた円の面積に等しい面積の正方形を構築するという問題です。
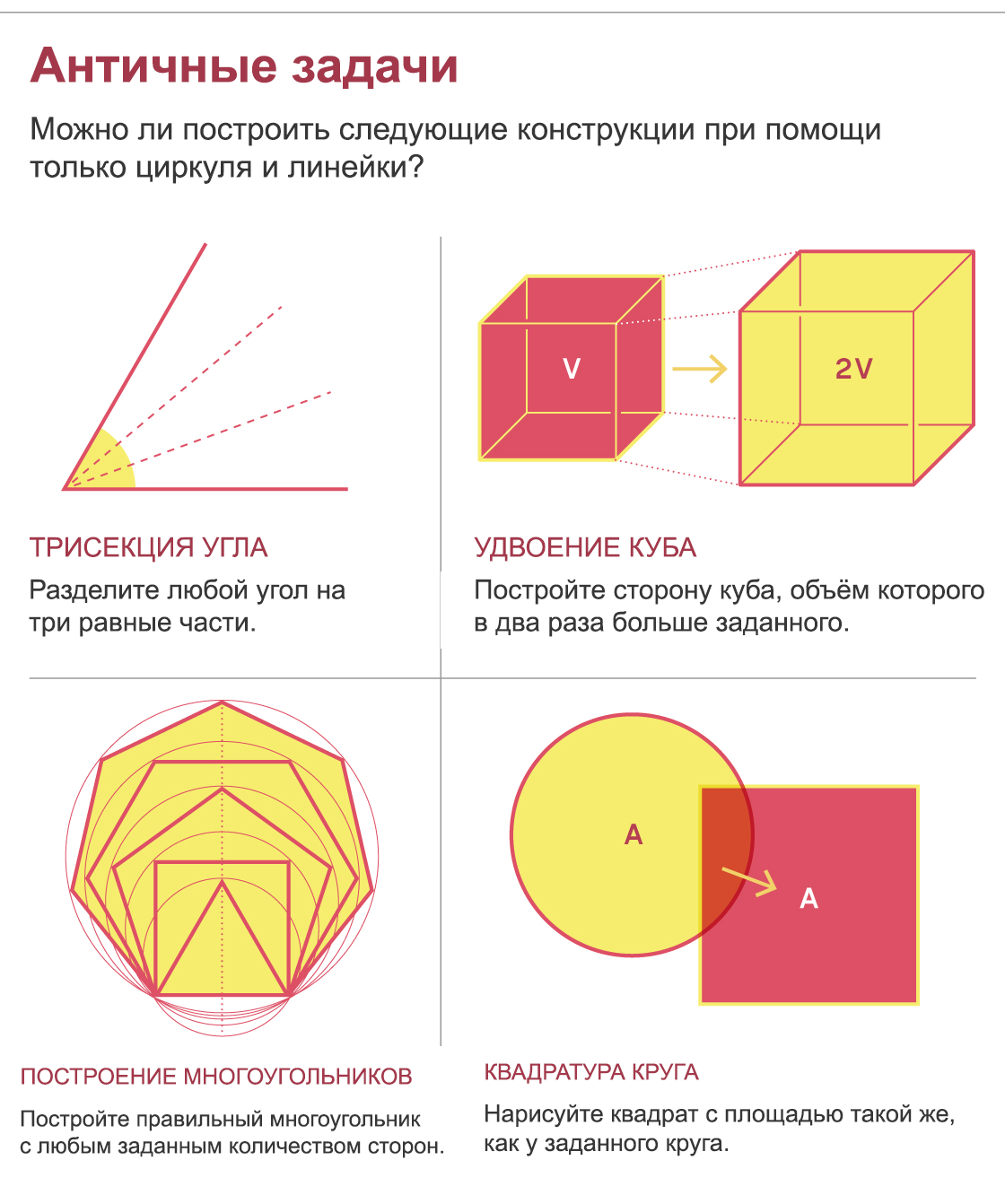
これらの問題は本質的に幾何学的ですが、解決できないという証拠はそうではありません。それらを解決することが不可能であることを実証するために、新しい数学が必要でした。
17世紀、ルネ・デスカルテスは根本的な発見をしました。コンパスと支配者だけに限定すると、どのような長さのセグメントも描くことができなくなります。長さ1の行から始める場合、整数、加算、減算、乗算、除算、および平方根(ゴールデンレシオなど)を使用して長さを表すことができる行のみを作成できます。
したがって、幾何学的問題を解決できないという証拠、つまり特定のオブジェクトを構築できないという証拠を見つけるための戦略の1つは、最終的な図の特定のセグメントの長さをこのように表現できないことを示すことです。しかし、これを厳密に示すためには、当時出現した代数が必要でした。
2世紀後、Descartesの同胞であるPierre Laurent Vanzelは、多項式(係数と変数の累乗の合計)とその根(多項式をゼロに等しくする変数)を使用して、これらの古典的な問題を攻撃しました。たとえば、キューブを2倍にする問題では、ユニットキューブの2倍のボリュームを持つキューブの側面は次のように等しくなければなりません。..。これは、多項式xの根である3 -2ため..。
1837年、Wanzelは、コンパスとルーラーを使用してセグメントを構築するには、その長さが因数分解できない多項式のルートである必要があり、その次数(変数の最高次数)が2の累乗であることを証明しました。たとえば、ゴールデンレシオは2次多項式x 2 -x-1のルートです。ただし、x 3 -2は3次多項式なので、構築することはできません。そのため、Wanzelは、キューブを2倍にすることは不可能であると結論付けました。
同様の方法で、彼は、古典的なツールを使用して任意の角度を3分割したり、特定の規則的なポリゴン(たとえば、7面のポリゴン)を構築したりすることは不可能であることを証明しました。興味深いことに、不可能性の3つの証拠すべてが同じページに投稿されました。アイザック・ニュートンやアインシュタインが自分の持っていたとしてannusミラビリス奇跡のページ- (奇跡の年)に、この状況はpaginaミラビリス呼び出すことができます。
残りの問題の不可能性を証明し、円を二乗するには、何か新しいことが必要でした。 1882年にフェルディナンドフォンリンデマンその超越性、つまりそれがどの多項式の根でもないことを証明することによって、重要なポイント(数πを構築できないこと)を証明しました。
これらの古典的な問題は、評判が悪いことに起因する可能性があり、数学者を不可能の鋭い岩に衝突させるサイレンであると見なすことができます。しかし、彼らは何世代にもわたる創造的な思想家にインスピレーションを与えてきたミューズだと思います。
同じことが、橋を渡るなどの単純な行為から生じる新しい不可能なタスクにも当てはまります。私の多くの学生のように、あなたが「橋の街」であるピッツバーグに住んでいると想像してみてください。冒険好きなサイクリストなら誰でも、家から乗車を始めると、ピッツバーグの主要な川を渡る22の橋のそれぞれを一度だけ渡って、家に帰れるのではないかと思うかもしれません。
1735年、プロシアの市長はレナードオイラーに同様の任務を設定しましたが、ケーニヒスベルク(現在のカリニングラード)にのみ適用されました。この都市の7つの橋は、川と島の3つの土手を接続しています。当初、オイラーはこの問題を数学的な問題ではないと却下しました。「この種の解決策は数学とはほとんど関係がなく、数学者が他の誰かではなくあなたにそれを与えることを期待する理由がわかりません。」
しかし、すぐにオイラーはこの問題を解決することが不可能であることを証明し、その過程で彼は配置の幾何学と呼ばれる数学の新しい領域を作成しました-今日私たちがトポロジーと呼んでいます。彼は、橋の正確な位置、土地の区画の形状など、特定の詳細に気づきました。 -重要ではありませんでした。彼らのつながりだけが重要でした。その後、数学者は、今日グラフと呼ばれるものを使用してオイラーの定式化を改良しました。接続性の概念は、ソーシャルメディア、インターネット、疫学、言語学、ルート計画などについて学ぶことの中核です。
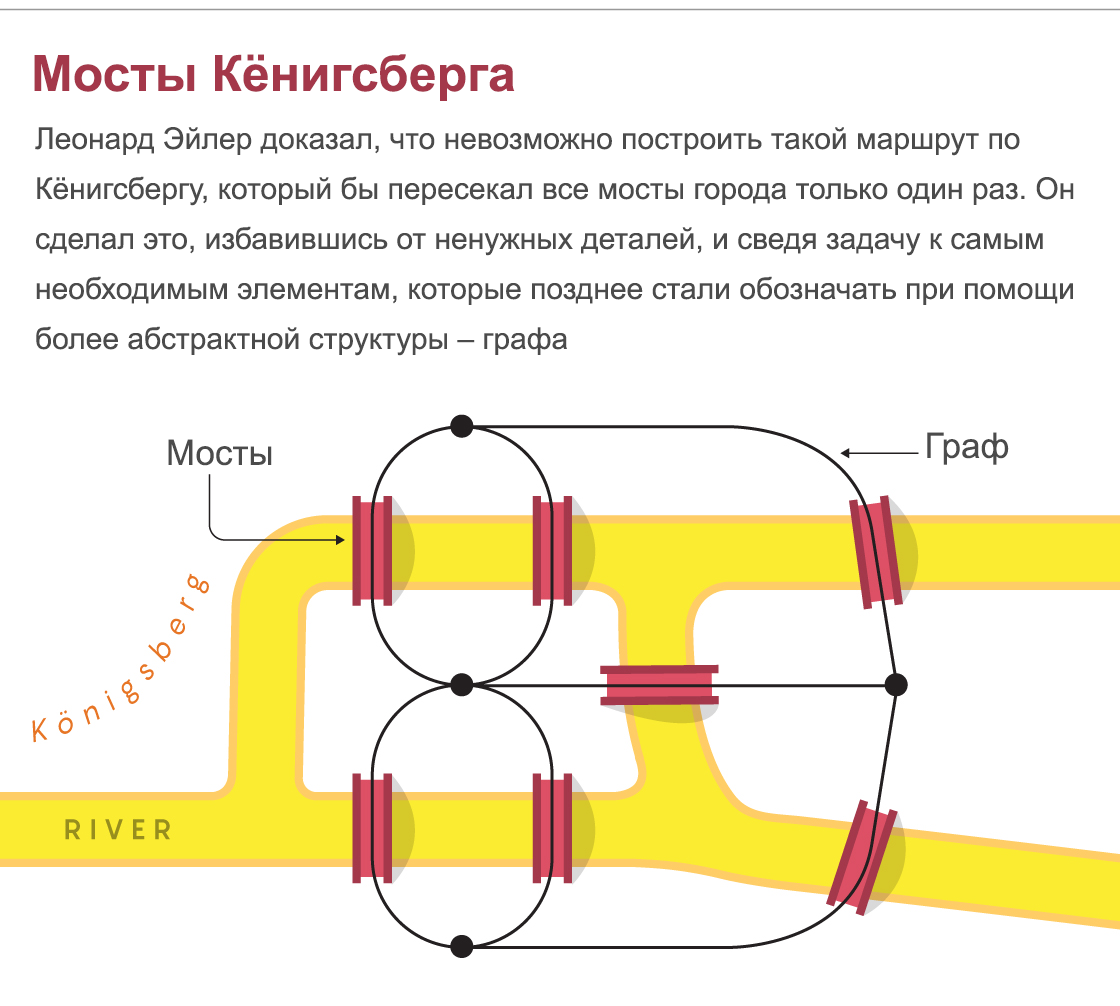
ケーニヒスベルク橋:レナード・オイラーは、ケーニヒスベルクに沿って、市内のすべての橋を一度だけ横断するルートを構築することは不可能であることを証明しました。彼はこれを不必要な詳細を取り除き、問題を最も必要な要素に減らし、後でより抽象的な構造、つまりグラフを使用して指定されるようになりました。
オイラーの証明は驚くほど単純でした。彼は、私たちが特定の土地に出入りするたびに、2つの橋をなくさなければならないと推論しました。したがって、各土地に偶数の橋を接続する必要があります。しかし、奇数の橋がケーニヒスベルクの各セクションにつながっていたため、そのようなルートを構築することは不可能でした。同様に、ピッツバーグのアレゲニー川にあるゲルス島につながる3つの橋は、目的のサイクルルートを構築することを不可能にします。
この問題が示すように、不可能性は抽象的な数学に限定されません。それらは現実世界の結果をもたらす可能性があります-時には政治的な結果さえも。
最近、数学者はゲリーメンダリングの概念に目を向けています。米国では、各国勢調査の後に、州は構成員をやり直す必要があります。しかし、時には与党は彼らの政治力を最大化するためにばかげた方法で彼らの境界を書き直します。
多くの州では、厳密な数学的定義がない「コンパクトな」地区が必要です。 1991年にダニエルPaulsbyとロバート・ポッパーは、提案4πA/ Pを2エリアAと周囲Pのコンパクトさを測定する方法として。これらの値は、丸い小教区の1から、周囲が長い変形した郡のほぼゼロまでの範囲です。
一方、ニコラス・ステファノプロスとエリック・マギーは、地区変更計画の政治的完全性の尺度として、2014年に「パフォーマンスギャップ」を導入しました。 2つの異なるゲリーマンダリング戦略は、構成員の反対派が投票の50%未満、または約100%を獲得することです。これらの戦術のそれぞれは、適切な候補者を失うか、そうでない人に投票を無駄にすることによって、反対派に投票を失います。効率のギャップは、失われた投票の相対的な数を表します。
これらの測定値は両方とも、ゲリーマンダリングを認識するのに役立ちます。しかし、2018年にはBorisAlekseevとDustinMixon「奇妙な形の郡では、小さな効率のギャップが達成されることがある」ことが証明されました。つまり、Paulsby-Popperの要件と、効率のギャップに関する正直さの両方を満たすような方法で郡を描くことは数学的に不可能です。
しかし、不正なジェリーマンダリング技術の検出と防止は急速に成長している分野であり、多くの才能ある研究努力を引き付けています。古代の問題やケーニヒスベルク橋の問題と同様に、ゲリーマンダリングの問題は創造性を刺激し、数学の発展に貢献すると確信しています。