4つの一般的なニューラルネットワークトレーニングオプティマイザを実装して比較します。インパルスオプティマイザ、rms伝搬、ミニバッチ勾配降下、および適応トルク推定です。リポジトリ、多くのPythonコードとその出力、視覚化、および式はすべてカットされています。

---

前書き

モデルは、いくつかのデータで実行されている機械学習アルゴリズムの結果です。モデルは、アルゴリズムによって学習されたものを表します。これは、トレーニングデータに対してアルゴリズムを実行した後も存続する「もの」であり、ルール、数値、およびアルゴリズムに固有で予測に必要なその他のデータ構造を表します。

オプティマイザーとは何ですか？

これに進む前に、損失関数が何であるかを知る必要があります。損失関数は、予測モデルが期待される結果（または値）をどれだけ適切に予測するかの尺度です。損失関数はコスト関数とも呼ばれます（詳細はこちら）。



トレーニング中は、機能の損失を最小限に抑え、パラメーターを更新して精度を向上させます。ニューラルネットワークのパラメータは通常、リンクの重みです。この場合、パラメータはトレーニング段階で調査されます。したがって、アルゴリズム自体（および入力データ）がこれらのパラメーターを調整します。詳細については、こちらをご覧ください。



したがって、オプティマイザーは、より良い結果を達成するための方法であり、学習のスピードアップに役立ちます。つまり、モデルを正しく迅速に実行し続けるために、重みや学習率などのパラメーターを微調整するために使用されるアルゴリズムです。これは、ディープラーニングで使用されるさまざまなオプティマイザーの基本的な概要と、そのモデルの実装を理解するための簡単なモデルです。このリポジトリのクローンを作成し、動作パターンを観察して変更を加えることを強くお勧めします。

いくつかの一般的に使用される用語：

• 誤差逆伝播法

バックプロパゲーションの目標は単純です。全体的なエラーの原因に応じて、ネットワーク内の各重みを調整します。各重みの誤差を繰り返し減らすと、適切な予測を行う一連の重みが得られます。損失関数の各パラメーターの勾配を見つけ、勾配を差し引くことによってパラメーターを更新します（詳細はこちら）。

• 勾配降下

勾配降下は、負の勾配値によって定義される最も急な降下に向かって繰り返し移動することによって関数を最小化するために使用される最適化アルゴリズムです。深層学習では、勾配降下を使用してモデルパラメータを更新します（詳細はこちら）。

• ハイパーパラメータ

モデルハイパーパラメータはモデルの外部の構成であり、その値をデータから推定することはできません。たとえば、隠れたニューロンの数、学習率などです。データから学習率を推定することはできません（詳細はこちら）。

• 学習率

学習率（α）は、損失関数の最小値に向かって移動しながら、各反復でのステップサイズを決定する最適化アルゴリズムの調整パラメーターです（詳細はこちら）。

人気のオプティマイザー

以下は、最も人気のあるSEOの一部です。

1. 確率的勾配降下（SGD）。
2. モメンタムオプティマイザー。
3. ルート平均二乗伝搬（RMSProp）。
4. 適応トルク推定（アダム）。

それぞれについて詳しく考えてみましょう。

1.確率的勾配降下（特にミニバッチ）

モデルを（純粋なSGDで）トレーニングし、パラメーターを更新するときに、一度に1つの例を使用します。ただし、ループには別のものを使用する必要があります。時間がかかります。したがって、ミニバッチSGDを使用します。



ミニバッチ勾配降下は、確率的勾配降下の堅牢性とバッチ勾配降下の効率のバランスをとろうとします。これは、深層学習で使用される勾配降下の最も一般的な実装です。ミニバッチSGDでは、モデルをトレーニングするときに、例のグループを取ります（たとえば、32、64の例など）。このアプローチは、すべての例ではなく、ミニバッチに対して1つのループしか必要としないため、より適切に機能します。ミニパッケージは反復ごとにランダムに選択されますが、なぜですか？ミニパケットがランダムに選択された場合、ローカルの最小値でスタックすると、ノイズの多いステップによってこれらの最小値が終了する可能性があります。なぜこのオプティマイザが必要なのですか？

• パラメータの更新レートは、単純なバッチ勾配降下よりも高く、局所的な最小値を回避することで、より信頼性の高い収束が可能になります。
• バッチ更新は、確率的勾配降下よりも計算効率の高いプロセスを提供します。
• RAMが少ない場合は、ミニパッケージが最適なオプションです。メモリとアルゴリズムの実装にすべてのトレーニングデータがないため、バッチ処理は効率的です。

ランダムなミニパケットを生成するにはどうすればよいですか？

def RandomMiniBatches(X, Y, MiniBatchSize):

    m = X.shape[0]  
    miniBatches = [] 
   
    permutation = list(np.random.permutation(m))
    shuffled_X = X[permutation, :]
    shuffled_Y = Y[permutation, :].reshape((m,1))   #sure for uptpur shape

    num_minibatches = m // MiniBatchSize 
    for k in range(0, num_minibatches):
        miniBatch_X = shuffled_X[k * MiniBatchSize:(k + 1) * MiniBatchSize,:]
        miniBatch_Y = shuffled_Y[k * MiniBatchSize:(k + 1) * MiniBatchSize,:]
        miniBatch = (miniBatch_X, miniBatch_Y)
        miniBatches.append(miniBatch)
    
    #handeling last batch
    if m % MiniBatchSize != 0:
        # end = m - MiniBatchSize * m // MiniBatchSize
        miniBatch_X = shuffled_X[num_minibatches * MiniBatchSize:, :]
        miniBatch_Y = shuffled_Y[num_minibatches * MiniBatchSize:, :]

        miniBatch = (miniBatch_X, miniBatch_Y)
        miniBatches.append(miniBatch)
    
    return miniBatches 

モデルのフォーマットはどうなりますか？



深層学習に不慣れな方のために、モデルの概要を説明します。これは次のようになります。

def model(X,Y,learning_rate,num_iter,hidden_size,keep_prob,optimizer):
    L = len(hidden_size)
    params = initilization(X.shape[1], hidden_size)
    for i in range(1,num_iter):
        MiniBatches = RandomMiniBatches(X, Y, 64)   # GET RAMDOMLY MINIBATCHES
        p , q = MiniBatches[2]
        for MiniBatch in MiniBatches:               #LOOP FOR MINIBATCHES

            (MiniBatch_X, MiniBatch_Y) = MiniBatch

            cache, A = model_forward(MiniBatch_X, params, L,keep_prob)             #FORWARD PROPOGATIONS
            cost = cost_f(A, MiniBatch_Y)                                          #COST FUNCTION
            grad = backward(MiniBatch_X, MiniBatch_Y, params, cache, L,keep_prob)  #BACKWARD PROPAGATION 
            params = update_params(params, grad, beta=0.9,learning_rate=learning_rate)
    return params

次の図では、SGDに大きな変動があることがわかります。垂直方向の動きは必要ありません：水平方向の動きだけが必要です。垂直方向の動きを減らし、水平方向の動きを増やすと、モデルの学習が速くなりますね。







不要な振動を最小限に抑える方法は？次のオプティマイザはそれらを最小化し、学習をスピードアップするのに役立ちます。

2.インパルスオプティマイザ

SGDや勾配降下には多くの躊躇があります。上下ではなく、前進する必要があります。モデルの学習率を正しい方向に上げる必要があり、それをモメンタムオプティマイザーで行います。







上の写真でわかるように、パルスオプティマイザーのグリーンラインは他のラインよりも高速です。大規模なデータセットと多くの反復がある場合、すばやく学習することの重要性がわかります。このオプティマイザーを実装する方法は？





βの通常の値は約0.9です。逆伝播パラメーターから



2つのパラメーター（vdWとvdb）を作成したことがわかります。値β= 0.9を考えると、方程式は次の形式になります。

vdw= 0.9 * vdw + 0.1 * dw
vdb = 0.9 * vdb + 0.1 * db

ご覧のとおり、vdwは、dwではなくvdwの以前の値に依存しています。レンダリングがグラフの場合、MomentumOptimizerが過去の勾配を考慮して更新をスムーズにしていることがわかります。これが変動を最小限に抑えることができる理由です。SGDを使用した場合、ミニバッチ勾配降下がたどる経路は収束に向かって振動しました。Momentum Optimizerは、これらの変動を減らすのに役立ちます。

def update_params_with_momentum(params, grads, v, beta, learning_rate):
    
    # grads has the dw and db parameters from backprop
    # params  has the W and b parameters which we have to update 
    for l in range(len(params) // 2 ):

        # HERE WE COMPUTING THE VELOCITIES 
        v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * grads['dW' + str(l + 1)]
        v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads['db' + str(l + 1)]
        
        #updating parameters W and b
        params["W" + str(l + 1)] = params["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]
        params["b" + str(l + 1)] = params["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]
    return params

リポジトリはこちら

3.ルート平均二乗スプレッド

ルートルート平均二乗（RMSprop）は、指数関数的に減衰する平均です。RMSpropの本質的な特性は、過去の勾配の合計だけに制限されるのではなく、最後のタイムステップの勾配にさらに制限されることです。RMSpropは、過去の「二乗則勾配」の指数関数的に減衰する平均に寄与します。RMSPropでは、平均を使用して垂直方向の動きを減らしようとしています。これは、平均をとると、合計が約0になるためです。RMSpropは、更新の平均を提供します。





ソース







以下のコードを見てください。これにより、このオプティマイザーを実装する方法の基本を理解できます。すべてSGDと同じで、更新機能を変更する必要があります。

def initilization_RMS(params):
    s = {}
    for i in range(len(params)//2 ):
        s["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
        s["db" + str(i)] = np.zeros(params["b" + str(i)].shape)
    return s

def update_params_with_RMS(params, grads,s, beta, learning_rate):
    
    # grads has the dw and db parameters from backprop
    # params  has the W and b parameters which we have to update 
    for l in range(len(params) // 2 ):
        # HERE WE COMPUTING THE VELOCITIES 
        s["dW" + str(l)]= beta * s["dW" + str(l)] + (1 - beta) * np.square(grads['dW' + str(l)])
        s["db" + str(l)] = beta * s["db" + str(l)] + (1 - beta) * np.square(grads['db' + str(l)])
        
        #updating parameters W and b
        params["W" + str(l)] = params["W" + str(l)] - learning_rate * grads['dW' + str(l)] / (np.sqrt( s["dW" + str(l)] )+ pow(10,-4))
        params["b" + str(l)] = params["b" + str(l)] - learning_rate * grads['db' + str(l)] / (np.sqrt( s["db" + str(l)]) + pow(10,-4))

    return params

4.アダムオプティマイザー

Adamは、ニューラルネットワークトレーニングで最も効率的な最適化アルゴリズムの1つです。これは、RMSPropとPulseOptimizerのアイデアを組み合わせたものです。Adamは、RMSPropのように、最初のモーメントの平均（平均）に基づいてパラメーターの学習率を適応させる代わりに、勾配の2番目のモーメントの平均も使用します。特に、アルゴリズムは、勾配と2次勾配の指数移動平均を計算し、パラメーターbeta1を計算してbeta2、これらの移動平均の減衰率を制御します。どうやって？

def initilization_Adam(params):
    s = {}
    v = {}
    for i in range(len(params)//2 ):

        v["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
        v["db" + str(i)] = np.zeros(params["b" + str(i)].shape)

        s["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
        s["db" + str(i)] = np.zeros(params["b" + str(i)].shape)
    return v, s
    
def update_params_with_Adam(params, grads,v, s, beta1,beta2, learning_rate,t):
    epsilon = pow(10,-8)
    v_corrected = {}                         
    s_corrected = {} 
    # grads has the dw and db parameters from backprop
    # params  has the W and b parameters which we have to update 
    for l in range(len(params) // 2 ):
        # HERE WE COMPUTING THE VELOCITIES 

        v["dW" + str(l)] = beta1 * v["dW" + str(l)] + (1 - beta1) * grads['dW' + str(l)]
        v["db" + str(l)] = beta1 * v["db" + str(l)] + (1 - beta1) * grads['db' + str(l)]

        v_corrected["dW" + str(l)] = v["dW" + str(l)] / (1 - np.power(beta1, t))
        v_corrected["db" + str(l)] = v["db" + str(l)] / (1 - np.power(beta1, t))


        s["dW" + str(l)] = beta2 * s["dW" + str(l)] + (1 - beta2) * np.power(grads['dW' + str(l)], 2)
        s["db" + str(l)] = beta2 * s["db" + str(l)] + (1 - beta2) * np.power(grads['db' + str(l)], 2)

        s_corrected["dW" + str(l)] = s["dW" + str(l)] / (1 - np.power(beta2, t))
        s_corrected["db" + str(l)] = s["db" + str(l)] / (1 - np.power(beta2, t))

        params["W" + str(l)] = params["W" + str(l)] - learning_rate * v_corrected["dW" + str(l)] / np.sqrt(s_corrected["dW" + str(l)] + epsilon)
        params["b" + str(l)] = params["b" + str(l)] - learning_rate * v_corrected["db" + str(l)] / np.sqrt(s_corrected["db" + str(l)] + epsilon)
    return params

ハイパーパラメータ

• β1（beta1）値はほぼ0.9
• β2（beta2）-ほぼ0.999
• ε-ゼロによる除算を防ぎます（10 ^ -8）（学習にあまり影響しません）

なぜこのオプティマイザー？



その利点：

• 簡単な実装。
• 計算効率。
• 低メモリ要件。
• 勾配の対角スケーリングに対して不変。
• データとパラメータの点で大規模なタスクに最適です。
• 非定常目的に適しています。
• 非常にノイズの多い、またはまばらな勾配のタスクに適しています。
• ハイパーパラメータは単純で、通常はほとんど調整する必要がありません。

モデルを作成して、ハイパーパラメータが学習をどのようにスピードアップするかを見てみましょう

学習を加速する方法の実践的なデモンストレーションをしましょう。この記事では、我々は他のものを（初期化、上映、説明できないだろうforward_prop、back_prop、勾配降下、およびように。D.）。トレーニングに必要な機能はすでにNumPyに組み込まれています。あなたがそれを見たいならば、ここにリンクがあります！

はじめましょう！

ここで説明するすべてのオプティマイザーで機能する汎用モデル関数を作成しています。



1.初期化：（



このfeatures_size 場合は12288）などの入力とサイズの非表示配列（[100,1]を使用）を受け取る初期化関数を使用してパラメーターを初期化し、この出力を初期化パラメーターとして使用します。別の初期化方法があります。この記事を読むことをお勧めします。

def initilization(input_size,layer_size):
    params = {}
    np.random.seed(0) 
    params['W' + str(0)] = np.random.randn(layer_size[0], input_size) * np.sqrt(2 / input_size)
    params['b' + str(0)] = np.zeros((layer_size[0], 1))
    for l in range(1,len(layer_size)):
        params['W' + str(l)] = np.random.randn(layer_size[l],layer_size[l-1]) * np.sqrt(2/layer_size[l])
        params['b' + str(l)] = np.zeros((layer_size[l],1))
    return params

2.順方向伝搬：



この関数では、入力はXであり、パラメーター、非表示レイヤーの範囲、およびドロップアウトは、ドロップアウト手法で使用されます。



ワークアウトで効果が見られないように、値を1に設定しました。モデルがオーバーフィットしている場合は、別の値を設定できます。ドロップアウトは偶数レイヤーにのみ適用します。



関数を使用して、各レイヤーのアクティベーション値を計算しますforward_activation。

#activations-----------------------------------------------
def forward_activation(A_prev, w, b, activation):
    z = np.dot(A_prev, w.T) + b.T
    if activation == 'relu':
        A = np.maximum(0, z)
    elif activation == 'sigmoid':
        A = 1/(1+np.exp(-z))
    else:
        A = np.tanh(z)
    return A


#________model forward ____________________________________________________________________________________________________________
def model_forward(X,params, L,keep_prob):
    cache = {}
    A =X

    for l in range(L-1):
        w = params['W' + str(l)]
        b = params['b' + str(l)]
        A = forward_activation(A, w, b, 'relu')
        if l%2 == 0:
            cache['D' + str(l)] = np.random.randn(A.shape[0],A.shape[1]) < keep_prob
            A = A * cache['D' + str(l)] / keep_prob
        cache['A' + str(l)] = A
    w = params['W' + str(L-1)]
    b = params['b' + str(L-1)]
    A = forward_activation(A, w, b, 'sigmoid')
    cache['A' + str(L-1)] = A
    return cache, A

3.逆伝播：



ここでは、逆伝播関数を記述します。grad（slope）を返します。gradパラメータを更新するときに使用します（それについて知らない場合）。この記事を読むことをお勧めします。

def backward(X, Y, params, cach,L,keep_prob):
    grad ={}
    m = Y.shape[0]

    cach['A' + str(-1)] = X
    grad['dz' + str(L-1)] = cach['A' + str(L-1)] - Y
    cach['D' + str(- 1)] = 0
    for l in reversed(range(L)):
        grad['dW' + str(l)] = (1 / m) * np.dot(grad['dz' + str(l)].T, cach['A' + str(l-1)])
        grad['db' + str(l)] = 1 / m * np.sum(grad['dz' + str(l)].T, axis=1, keepdims=True)
        if l%2 != 0:
            grad['dz' + str(l-1)] = ((np.dot(grad['dz' + str(l)], params['W' + str(l)]) * cach['D' + str(l-1)] / keep_prob) *
                                 np.int64(cach['A' + str(l-1)] > 0))
        else :
            grad['dz' + str(l - 1)] = (np.dot(grad['dz' + str(l)], params['W' + str(l)]) *
                                       np.int64(cach['A' + str(l - 1)] > 0))

    return grad

オプティマイザの更新機能はすでに見てきたので、ここで使用します。SGDの説明から、モデル関数にいくつかの小さな変更を加えましょう。

def model(X,Y,learning_rate,num_iter,hidden_size,keep_prob,optimizer):
    L = len(hidden_size)
    params = initilization(X.shape[1], hidden_size)
    costs = []
    itr  = []

    if optimizer == 'momentum':
        v = initilization_moment(params)

    elif optimizer == 'rmsprop':
        s = initilization_RMS(params)

    elif optimizer == 'adam' :
        v,s = initilization_Adam(params)

    for i in range(1,num_iter):
        MiniBatches = RandomMiniBatches(X, Y, 32)   # GET RAMDOMLY MINIBATCHES
        p , q = MiniBatches[2]
        for MiniBatch in MiniBatches:               #LOOP FOR MINIBATCHES

            (MiniBatch_X, MiniBatch_Y) = MiniBatch

            cache, A = model_forward(MiniBatch_X, params, L,keep_prob)     #FORWARD PROPOGATIONS
            cost = cost_f(A, MiniBatch_Y)                                  #COST FUNCTION
            grad = backward(MiniBatch_X, MiniBatch_Y, params, cache, L,keep_prob) #BACKWARD PROPAGATION 

            if optimizer == 'momentum':
                params = update_params_with_momentum(params, grad, v, beta=0.9,learning_rate=learning_rate)

            elif optimizer == 'rmsprop':
               params = update_params_with_RMS(params, grad, s, beta=0.9,learning_rate=learning_rate)

            elif optimizer == 'adam' :
                params = update_params_with_Adam(params, grad,v, s, beta1=0.9,beta2=0.999,  learning_rate=learning_rate,t=i)                                         #UPDATE PARAMETERS
            elif optimizer == "minibatch":
                params = update_params(params, grad,learning_rate=learning_rate) 

           
        
        if i%5 == 0:
            costs.append(cost)
            itr.append(i)
            if i % 100 == 0 :
                print('cost of iteration______{}______{}'.format(i,cost))
    return params,costs,itr

ミニパックでのトレーニング

params, cost_sgd,itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='minibatch')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

ミニパッケージでアプローチするときの結論：

cost of iteration______100______0.35302967575683797 
cost of iteration______200______0.472914548745098 
cost of iteration______300______0.4884728238471557 
cost of iteration______400______0.21551100063345618
 
train_accuracy------------ 0.8494208494208494

パルスオプティマイザートレーニング

params,cost_momentum, itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='momentum')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

パルスオプティマイザ出力：

cost of iteration______100______0.36278494129038086 
cost of iteration______200______0.4681552335189021 
cost of iteration______300______0.382226159384529 
cost of iteration______400______0.18219310793752702 train_accuracy------------ 0.8725868725868726

RMSpropを使用したトレーニング

params,cost_rms,itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='rmsprop')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

RMSprop出力：

cost of iteration______100______0.2983858963793841 
cost of iteration______200______0.004245700579927428 
cost of iteration______300______0.2629426607580565 
cost of iteration______400______0.31944824707807556 train_accuracy------------ 0.9613899613899614

アダムとのトレーニング

params,cost_adam, itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='adam')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

アダムの結論：

cost of iteration______100______0.3266223660473619 
cost of iteration______200______0.08214547683157716 
cost of iteration______300______0.0025645257286439583 
cost of iteration______400______0.058015188756586206 train_accuracy------------ 0.9845559845559846

2つの精度の違いを見たことがありますか？同じ初期化パラメーター、同じ学習率、同じ反復回数を使用しました。オプティマイザーだけが異なりますが、結果を見てください！

Mini-batch accuracy : 0.8494208494208494
momemtum accuracy   : 0.8725868725868726
Rms accuracy        : 0.9613899613899614
adam accuracy       : 0.9845559845559846

モデルのグラフィック視覚化





コードに疑問 がある場合は、リポジトリを確認できます。

概要

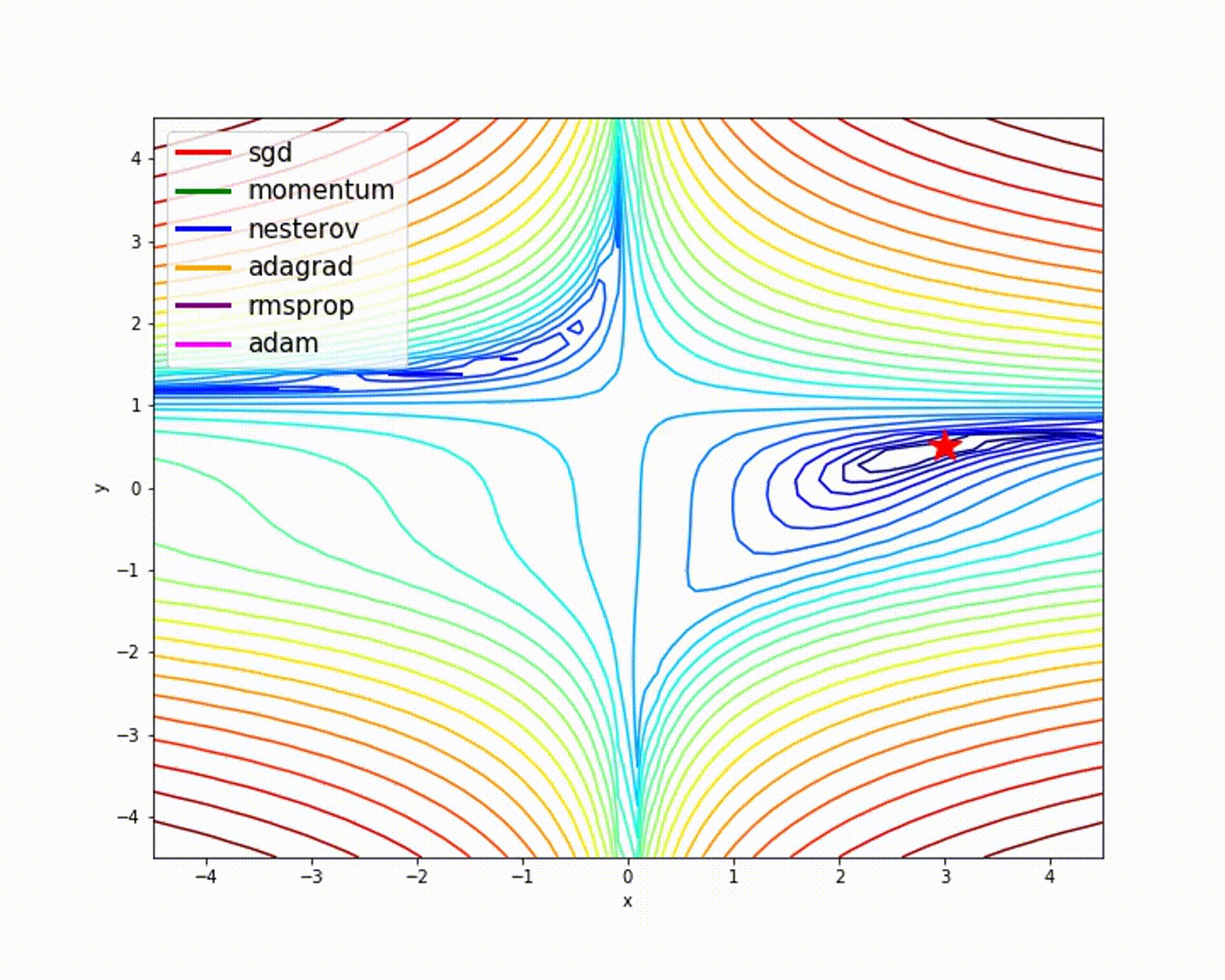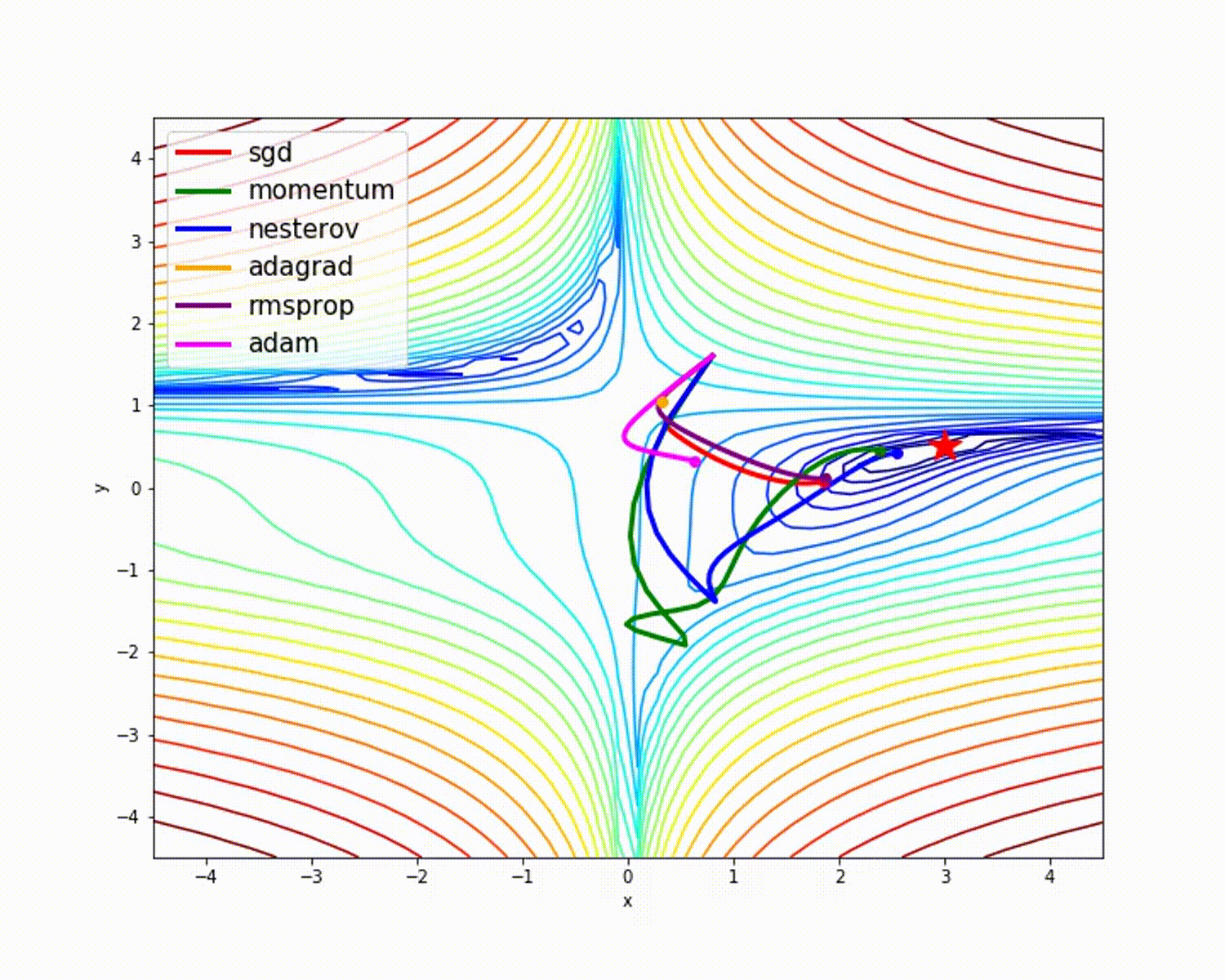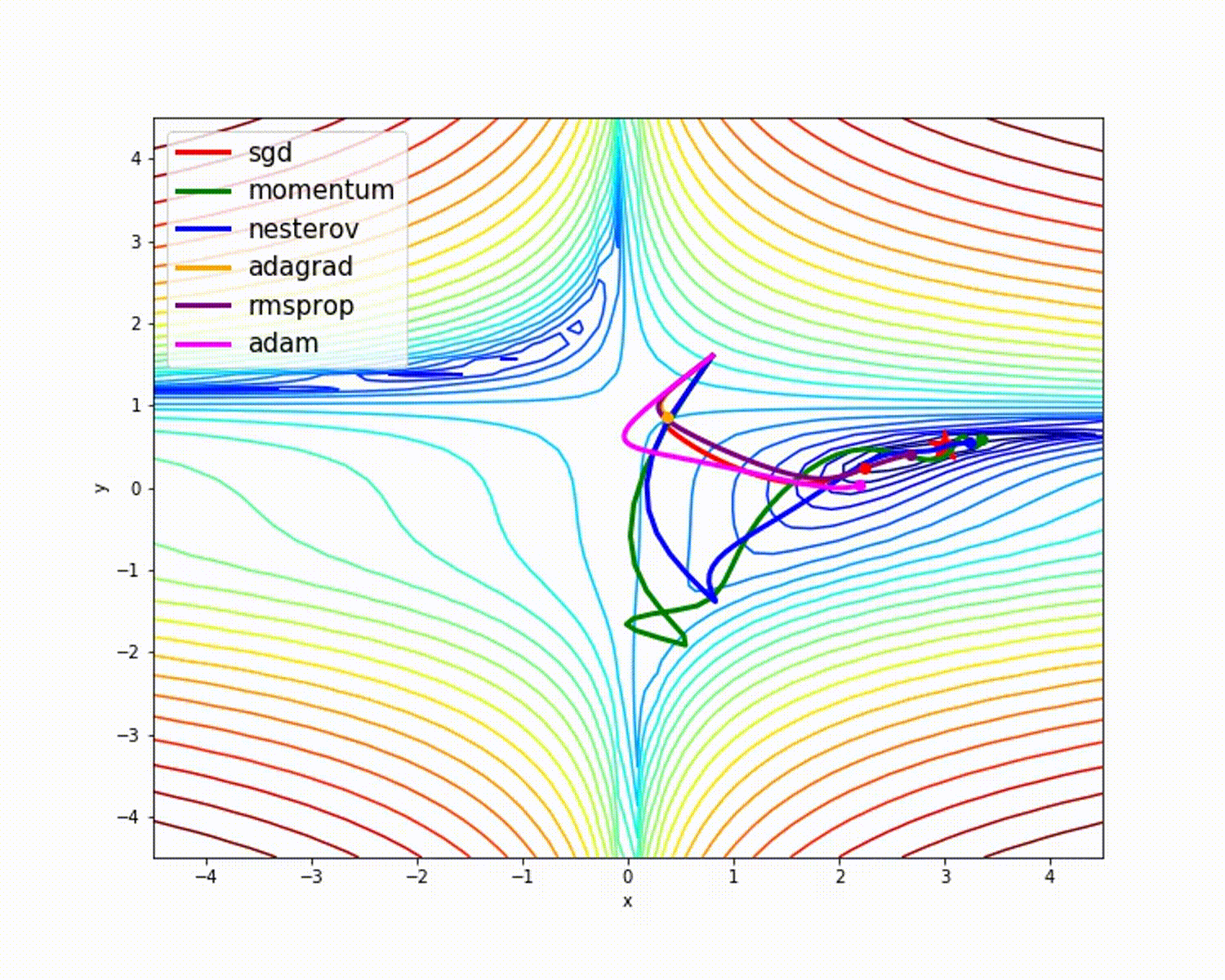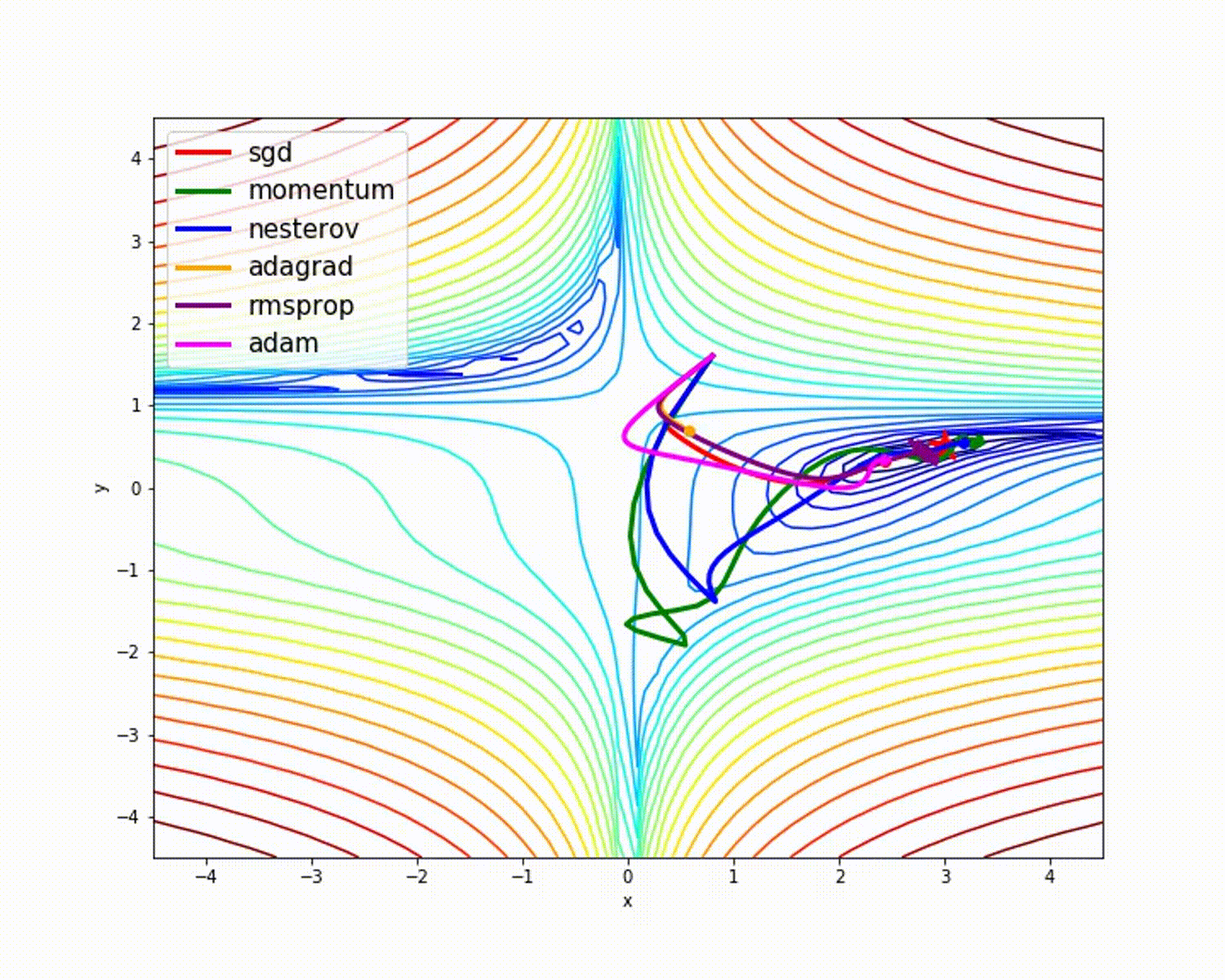
ソース

これまで見てきたように、Adamオプティマイザーは他のオプティマイザーと比較して優れた精度を提供します。上の図は、モデルが反復を通じてどのように学習するかを示しています。MomentumはSGD速度を示し、RMSPropは更新されたパラメーターの重みの指数平均を示します。上記のモデルでは使用するデータが少なくなっていますが、大規模なデータセットと多くの反復を処理する場合、オプティマイザーのメリットが大きくなります。オプティマイザーの基本的な考え方について説明しました。これにより、オプティマイザーについてさらに学び、使用する動機が得られることを願っています。





ニューラルネットワークとディープマシンラーニングの見通しは非常に大きく、最も控えめな見積もりによると、世界への影響は、19世紀の産業への電力の影響とほぼ同じです。誰よりも早くこれらの見通しを評価する専門家は、進歩のリーダーになるチャンスがあります。そのような人々のために、私たちはプロモーションコードHABRを作成しました。これは、バナーに示されているトレーニング割引にさらに10％を与えます。

• 機械学習コース
• コース「データサイエンスのための数学と機械学習」
• 上級コース「MachineLearningPro + DeepLearning」
• データサイエンスのオンラインブートキャンプ
• データアナリストの職業をゼロからトレーニングする
• データ分析オンラインブートキャンプ
• データサイエンスの専門家をゼロから教える
• Python forWeb開発コース

おすすめ記事

• オンラインコースなしでデータサイエンティストになる方法
• 450
• Machine Learning 5 9
• : 2020
• Machine Learning Computer Vision