
4次の多項式の根を見つける方法はいくつかあります。
ただし、パラメータを使用した式である係数を使用して方程式を解くにはあまり便利ではありません。
インスタグラム
1.次数4の方程式を解くための式
根の合計がゼロに等しい4次の方程式を考えてみましょう。係数は実数でも複雑でもかまいません。

次の2つの正方形の積は、考慮されている4次の方程式と同じです。
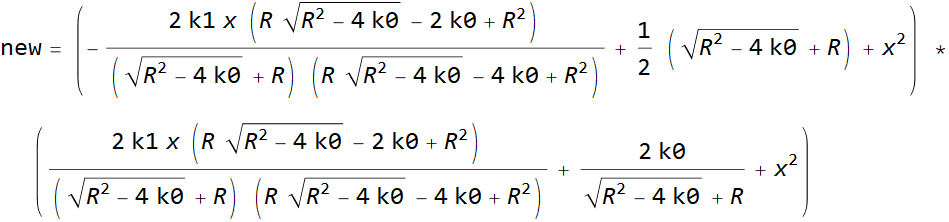
R値は、次の3次方程式の解です。
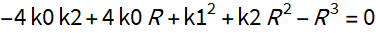
完全二乗の差に展開して4次の方程式を解くと、ほぼ同じ方程式が現れます。この三次方程式を補助と呼びます。
新しい2つの正方形の積を計算してみましょう。
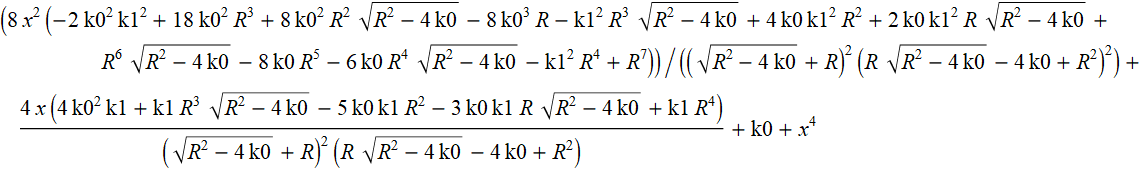
同じですが、xの累乗(累乗の降順)での係数の形式です。
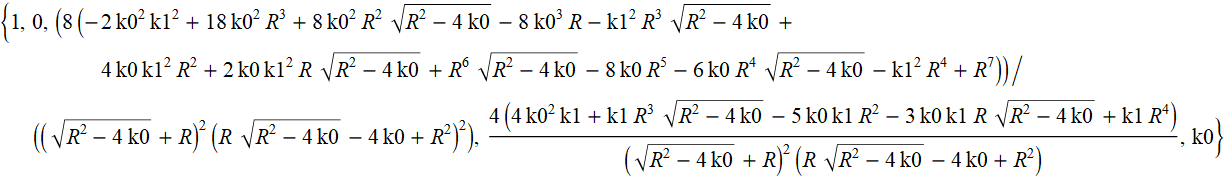
xの2乗と1乗の係数の式を単純化してみましょう。
上記の式は、xの1次に対するものです。

その結果、k1が得られます。
上記の式は、xの2乗に対するものです。

または

、式をR ^ 3に代入すると、
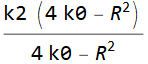
Ork2が得られ ます。
したがって、newは4次の方程式と同じであり、その根の合計はゼロに等しくなります。
補助三次方程式の問題は残っています。
もちろん、従来の解決方法を使用することもできます。しかし、その後、方程式を正規の形式に変換し、係数の値に応じて3つのソリューションを個別に検討する必要があります。これは、パラメーターを持つ式である係数には必ずしも便利ではありません。
2.チャーンハウゼン変換法による3次方程式の解法
あまり普及していないChirnhausen変換法による3次方程式の解法を考えてみましょう。
そこで、 元の方程式
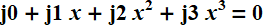
をチャーンハウゼン法で解きます。
この方法の本質は、次の変換にあります。
1. yの式を導入します
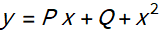
。2。項目1の等式の両側にxを掛けます。

次に、x ^ 3の
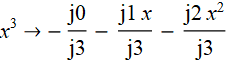
式を次の式に置き換え ます。

一般に、セクション2で説明されている変換は同一ではありません。しかし、元の方程式の根であるxの値だけを興味深いと考えると、これらの変換は準同一と見なすことができます。そして、yは元の方程式の根に対応する式で表されます。
3. 3次方程式の場合、項目2の操作がもう一度実行されます。その結果、元の方程式の根に対応する3つの非ゼロ解を持つxの3つの方程式のシステムが得られます。係数xから行列
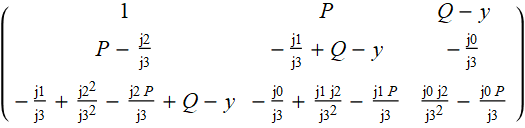
4を形成 します。yの3次式で表される行列の決定要因を見つけます。
決定要因がゼロに等しいことを保証する値を計算します。
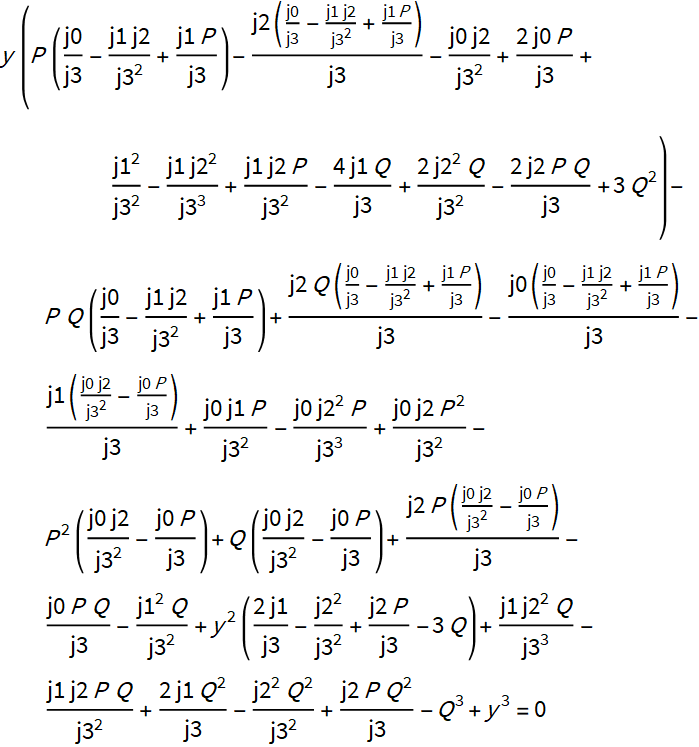
5. yに関する式には、2つのパラメーターPとQがあります。yの2次と1次の係数がゼロになるように計算してみましょう。
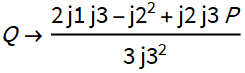
任意のP
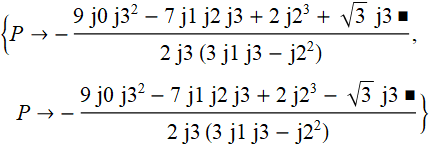
、ここで

6。その結果、y

7の3つの複数の根を持つ 方程式があります。既知のy、P、Qを持つ2次方程式を解くことが残ってい
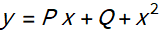
ます。解の1つは、元の方程式の解になります。
3.補助3次方程式を解くためのパラメーター
係数の特定の値については、すべてがそれほど怖くはありません。
4次方程式を解くための式には、補助3次方程式のルートRが1つだけ必要であることに注意してください。
補助方程式の特定の係数については

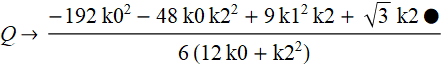
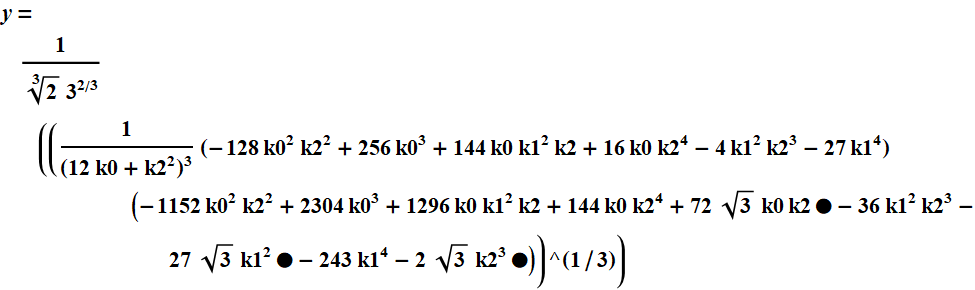

、次のようになります。4次の方程式を解くための式を使用する場合は、「メソッドftvmetrics」を参照する必要があります。
直接に興味深いタスクを送信 Instagramの。