地球が球体ではなく、形が違うとしたら、どんな生活になるのだろうと思ったことはありませんか?私たちは、太陽系を通る惑星のスムーズな走りと、地球の回転対称性のおかげで楽しむことができるゆっくりとした日没を当然のことと考えています。さらに、球体地球を使用すると、ポイントAからポイントBに到達するための最速の方法を決定できます。これらの2つのポイントを通過し、球を半分にカットする円を歩くだけです。航空機のルートを計画し、衛星の軌道を計算するために、測地パスと呼ばれるこれらの最短パスを使用します。

しかし、私たちがキューバに住んでいたらどうなるでしょうか?私たちの世界はもっと揺れ動き、地平線は曲がり、A地点からB地点までの最短経路を見つけるのは難しくなります。立方体での生活を想像するのに多くの時間を費やすことはないかもしれませんが、数学者は、さまざまな形で私たちの旅行がどのように見えるかを研究します。そして、 十二面体に関する基本的な質問の1つに対する最近の解決策は、一般に、何千年もの間私たちの目の前にあったオブジェクトの見方を変えました。
特定のジオメトリックボディの最短パスを前後に(立方体の周りのあるポイントから同じポイントに)見つけることは、簡単な作業のように思えるかもしれません。結局のところ、あなたは間違いなくあなたが始めたところに戻るでしょう?
実際、それはあなたが歩いている形や体に依存します。これが球の場合は、はい。 (もちろん、地球は理想的な球体ではなく、その表面は完全に滑らかではないという事実を省略しています。)球体では、パスは直線の「大きな円」、測地線、たとえば赤道に沿って繰り返されます。赤道を一周すると、約25,000マイル後に、完全な円を完成して、開始した場所に戻ります。
立方体の世界では、測地線はそれほど明白ではありません。それぞれの面が平らなので、片方の面でまっすぐな道を見つけるのは簡単です。しかし、もしあなたが周りの立方体の世界を歩き回っていたら、あなたが端に達したときにどのようにまっすぐ歩き続けるでしょうか?
私たちの質問への答えを説明する古い面白い数学の問題があります。立方体の片隅にいて、反対側の隅に行きたがっているアリを想像してみてください。点Aから点Bまでの立方体の表面上の最短経路は何ですか?
アリがたどる可能性のある多くの異なる経路を想像してみてください。

しかし、どれが最短ですか?問題を解決するための独創的な方法があります。キューブを平らにしましょう!
立方体が紙でできている場合は、端に沿って切り取り、シートを平らにして、この展開されたパターンを得ることができます。

このような平坦な世界では、AからBへの最短経路を見つけるのは簡単です。それらの間に直線を引くだけです。

キューブの世界で測地線がどのようになるかを確認するには、キューブを元に戻します。これが私たちのショートカットです。

立方体の各面が平らであるため、立方体の「位置合わせ」が機能します。そのため、エッジに沿ってボディを展開しても、歪みは発生しません。 (球を歪ませずに平らにすることはできないため、球を「展開」するこの試みは機能しません。)
立方体上で直線のパスがどのように見えるかがわかったので、直線のパスをたどって最初の場所に戻ることができるかどうかの質問に戻りましょう。球体とは異なり、立方体では、すべての直線経路が最初に戻るわけではありません。
しかし、そのような往復ルートは可能です。 1つのトリックで!アリは上で示したパスを続行して、開始した場所に戻ることができることに注意してください。立方体では、完全な円がダイヤモンドのように見えるパスを作成します。

このパスを(前後に)たどると、アリは開始点に戻る前に別の頂点(点B)を通過する必要があります。これが問題です。同じ頂点で開始および終了するすべての直線パスは、立方体の別の頂点を通過する必要があります。
これは、5つの正多面体のうちの4つに当てはまることがわかります。立方体、四面体、八面体、および二十面体では、同じ頂点で開始および終了する直線パスは、パスに沿って他の頂点を通過する必要があります。数学者はこれを5年前に証明しましたが、十二面体は彼らのリストにありませんでした。少し後でこれに戻ります。

測地線に関するこの事実が5つの正多面体のうちの4つに当てはまる理由を理解するために、タンブリング法を使用して、この方法をよりよく示すことができる四面体の世界に切り替えます。
四面体の上部から開始し、端に沿って直線で歩くことを想像してみてください。パスが下端から始まるように四面体を配置します。
:私たちはエッジが発生したときに、私たちのパスを下回ることが判明した面に沿って続くように、私たちは四面体を反転

このような回転は、我々は、キューブを展開に行うだろうと同じように私たちのパスを追跡することを可能にする:

の軌道を上記の回転は、四面体の表面上のこのパスを表しています。

四面体の5つのターンは、ルートが交差する追加の5つの面に対応します。
これで、四面体の表面上の任意のパスを、この「回転する」空間内のパスとして想像できます。開始点Aを定義し、数ターン後にどこで終了するかを見てみましょう。
パスがポイントAを離れると、四面体は反対側に落下します。これにより、ポイントAが地面から浮き上がります。

頂点Aは、回転する世界で一時的に上昇します。通常、回転スペースを作成するときにポイントAの位置を指定しませんが、下を見下ろした場合に表示される可能性のある場所は次のとおりです。

私たちの道が続くにつれて、四面体は再び落ちます。彼は2つの可能な方向のいずれかでそれを行うことができますが、いずれにせよ、Aは再び一番下にあります。
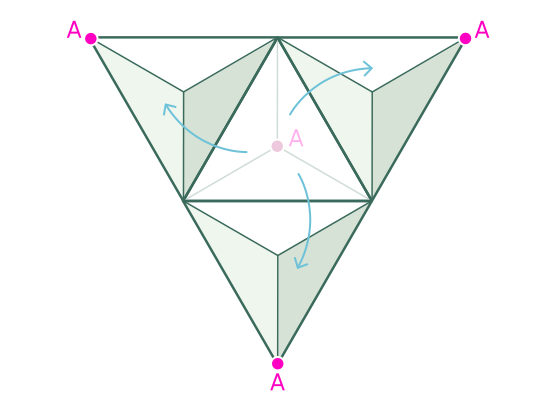
四面体をすべての可能な方向に落下させると、次のような宙返りが

発生します。四面体の正三角形の面が互いに一致するため、一種の格子になります。

この三角形のグリッドは、回転する世界について2つの興味深いことを示しています。まず、四面体の頂点が着地できるすべての点は、「格子点」(図に示されている)または整数座標の点です。これは、座標系の1つの単位が四面体の1つのエッジの長さに等しいためです。
次に、Aがどこに到達するかを確認します。Aの
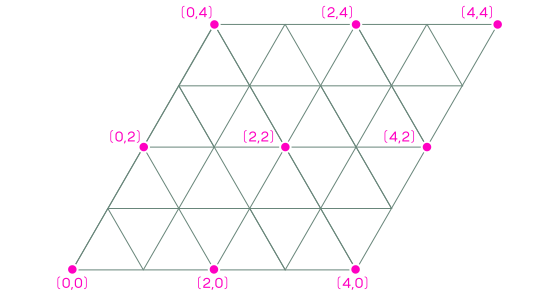
座標は常に偶数です。 Aがダウンしているときはいつでも、2回のスピンの後にそこに戻るので、Aのすべての可能な着陸地点は、スピンの各方向に2つのリブの長さの間隔で配置されます。
それでは、これが測地線について何を言っているか見てみましょう。ポイントAで開始および終了する四面体のパスは、ポイントA(0,0)で開始し、別のポイントAで終了する回転空間の直線セグメントになることを思い出してください。パスの開始点と終了点がシングルAで一致します、パスの真ん中に何がありますか?
紛らわしい座標系でも、線分の中点を計算するための標準的な式は機能するため、端点の座標に基づいてその座標を見つけることができます。
始点の両方の座標が0で、終点の両方の座標が偶数であるため、中央の座標は整数です。つまり、中央はラティスのポイントの1つになります。これは、前述のように、回転空間の三角形の頂点に対応することを意味します。
たとえば、(0,0)から(4,2)へのパスには、中点(2,1)があります。これは、グリッド内でマークされたラティスポイントです。

四面体の表面では、Aから戻るパスは別の頂点を通過する必要があることがわかります。
Aのすべての可能な「ランディング」には偶数の座標があるため、Aで開始および終了するすべての測地パスの中点はグリッドポイントに対応します。これは、四面体の表面上のAからAまでのすべての測地線が別の頂点を通過する必要があることを証明しています。
この単純な 推論は、数学者のダイアナデイビス、ビクタードッズ、シンシアトラウブ、ジェドヤングによって2015年に詳しく説明されました。
彼らは、似ているがはるかに複雑な方法を使用して、立方体について同じことを証明しました。翌年、DmitryFuksが 確認しました八面体と二十面体の結果。このため、四面体、立方体、八面体、二十面体の場合、頂点からそれ自体に戻る直線パスがなく、別の頂点を通過しないことがわかっています。
しかし、十二面体の表面にそのような経路が存在するかどうかの問題は、数学者のJayadev Atreya、David Avlikino、およびPatrickHooperが実際に可能であると証明した2019年まで開いたままでした 。実際、彼らは十二面体の表面に、他の頂点を通過せずに同じ頂点で開始および終了する無限に多くの直線経路を見つけました。
これは、十二面体のスキャンに描かれた、明白な視界に隠れているそれらの1つです。

正多面体は、多くの共通点があるため、何千年もの間一緒に研究されてきました。しかし今、私たちは十二面体について何か新しいことを知っており、これはそれを他の物体と明確に区別しています。
この不思議な発見は、数学的対象をどれほどよく理解しても、学ぶべきことが常にあることを示しています。問題から解決への道は必ずしも簡単ではないことを覚えておくことは重要です!
タスク
1.立方体の辺の長さが1の場合、1つの頂点から反対側へのアリの最短経路はどれくらいですか。
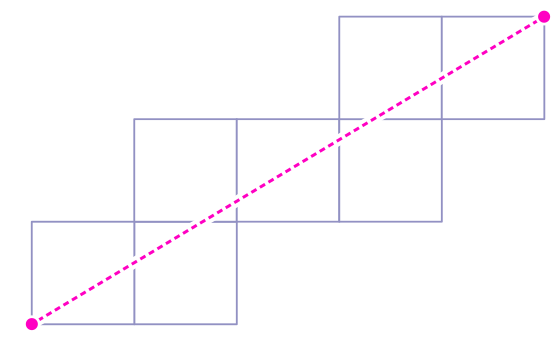
2.下の図が立方体の回転パスになれない理由を説明してください。

3.立方体を「回転」させる際の問題の1つは、点Aに立方体の終了位置に関連付けられた一意の終了位置がないことです。たとえば、立方体が同じ場所にあり、赤または青のパスに沿って回転している場合でも、点Aは異なる位置にあります。赤と青の弾道に沿って曲がった後、Aがどこにあるかを決定します。

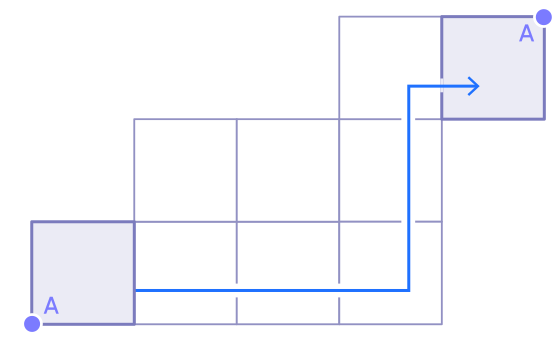
4.これは立方体の回転の軌道です。
点Aから始めて、立方体の表面にパスを描画します。

回答
クリックして回答1を表示
パスは、脚が1と2の直角三角形の斜辺です。

ピタゴラスの定理によれば、ABの長さは√5です。

ピタゴラスの定理によれば、ABの長さは√5です。
クリックして回答2を表示
, 1 . , , .

, «» , .

, «» , .
, 3
.

, .


, .
, 4

