人工ニューラルネットワーク。パート1

ニューロン

この記事では、人工ニューロンがどのように機能するかの基本を学びます。以降の記事では、ニューラルネットワークの基本を学び、Pythonで簡単なニューラルネットワークを記述します。

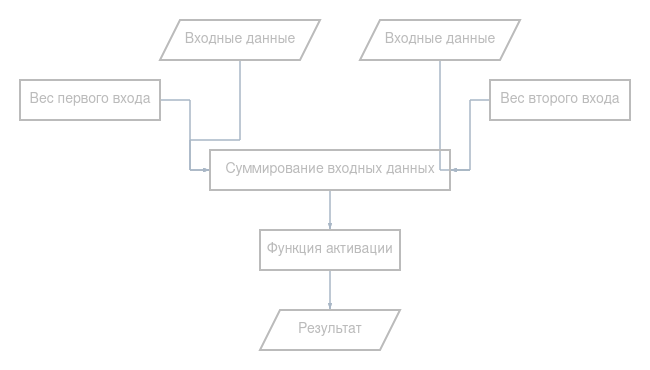
ニューラルネットワークは相互に接続されたニューロンで構成されているため、ニューロンはニューラルネットワークの主要部分です。ニューロンは2つのアクションのみを実行します。入力データに重みを掛けて加算し、バイアスを加算します。2番目のアクションはアクティブ化です。

次に、入力データ、重み、バイアス、および活性化関数について詳しく説明します。

入力データは、ニューロンが以前のニューロンまたはユーザーから受け取るデータです。

重みはニューロンの各入力に割り当てられ、最初は乱数が割り当てられます。ニューラルネットワークをトレーニングすると、ニューロンと変位の値が変化します。重みは、ニューロンに供給される入力データで乗算されます。

初期バイアスの重みと同様に、オフセットは各ニューロンに割り当てられます。これらは乱数です。オフセットにより、ニューラルネットワークのトレーニングがより簡単かつ迅速になります。

ニューラルネットワークで使用する活性化関数は、シグモイドと呼ばれます。シグモイド式は次のとおりです。

この関数は、0から1の範囲の-∞から+∞までの任意の数値をラップします。

ニューロンが実行するタスクを数学的に説明すると、次の2つの式が得られます。

f（x）-活性化関数

x-入力データと重みの積とバイアスの合計

i-入力データの配列

w -

b -

j -

python.

numpy. Linux Window:

pip install numpy
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

import numpy as np
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

Neuron, :

class Neuron:
    def __init__(self, number_of_weights = 1):

        self.w = np.random.normal(size=number_of_weights)
        self.b = np.random.normal()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

, , . . :

def activate(self, inputs):
        
        x = np.dot(self.w, inputs) + self.b
        
        return sig(x)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

, . :

def sig(x):
  return 1 / (1 + np.exp(-x)) 
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

Math.py

numpy:

import numpy as np
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

Neuron.py. Neuron.py Math.py:

from Math import *
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

2 :

Neuron.py

import numpy as np

from Math import *

class Neuron:
    def __init__(self, number_of_weights = 1):

        self.w = np.random.normal(size=number_of_weights)
        self.b = np.random.normal()
        
    def activate(self, inputs):
        
        x = np.dot(self.w, inputs) + self.b
        
        return sig(x)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

Math.py

import numpy as np

def sig(x):
  return 1 / (1 + np.exp(-x))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

.

, :

1. 
   
   
   
   

2. ,

   
   
   
   
   

3. Python

   
   
   
   
   

- .