クイックダブル比較

昨日 、doubleの高速解析に関する記事がありました。その作者のブログにアクセスして、別の興味深いトリックを見つけました 。浮動小数点数を比較するときは、NaNに特別な注意を払う必要があります（8年前に私はそれらについてより詳細に 書きました）。しかし、比較されている数値が確かにNaNでない場合は、プロセッサよりも速く比較できます。



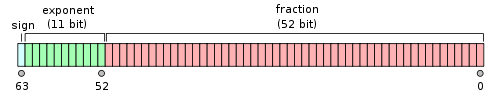
正の倍精度を比較するのは非常に簡単です。正規化により、指数が異なる数ほど指数が大きい数が大きくなり、同じ指数を持つ数ほど仮数が大きい数が大きくなることが保証されます。 IEEE 754標準では、指数が上位ビットに注意深く配置されているため、正の倍精度浮動小数点数は単純にint64_tと比較できます。







負の数はもう少し複雑です。負の数は直接コードに格納され ますが、int64_tは相補コードに格納され ます。これは、整数比較を使用するには、doubleの下位63ビットを反転する必要があることを意味します（これにより、-0。<+0。になります。これは標準に対応していませんが、実際には問題はありません。 ）。明示的な高次ビットチェックと条件分岐は、整数比較にジャンプすることのすべての利点を破壊します。しかし、もっと簡単な方法があります！

inline int64_t to_int64(double x) {
	int64_t a = *(int64_t*)&x;
	uint64_t mask = (uint64_t)(a >> 63) >> 1;
	return a ^ mask;
}

inline bool is_smaller(double x1, double x2) {
	return to_int64(x1) < to_int64(x2);
}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

a>>63



64ビットすべてを符号ビットのコピーで埋めてから >>1



、最上位ビットをクリアします。



Daniel Lemireのブログのコードはわずかに異なります（計算の複雑さは同じです）が、私のバージョンでは、次のような便利なプロパティが保持されています。 to_int64(0.) == 0