👯 🐷 🤐 時系列。簡単な解決策 👨🏿‍🍳 🚭 🔢

こんにちは、Habr！

この記事では、いくつかの簡単な時系列予測アプローチを見ていきます。

私の意見では、この記事で紹介されている資料は、MIPTとYandexの「データ分析の応用問題」コースの最初の週をよく補完しています。示されたコースでは、一連のダイナミクスを予測する問題を解決するのに十分な理論的知識を得ることができ、資料の実用的な統合として、scipyライブラリのARIMAモデルを使用してロシア語で給与予測を生成することが提案されています来年の連盟。この記事では、給与予測も生成しますが、同時にscipyライブラリではなく、ライブラリを使用します。 sklearn。秘訣は、 scipyにはすでにARIMAモデルがありますが、 sklearnには既製のモデルがないため、ペンを使って一生懸命作業する必要があります。したがって、問題を解決するためには、ある意味で、モデルが内部からどのように機能するかを理解する必要があります。また、追加資料として、この記事では、pytorchライブラリの単層ニューラルネットワークを使用して予測問題を解決しています。

すべてのコードはで書かれている のpython 3で jupyterノート。さらに、 ノートブックは、賃金に関するデータの代わりに、砂糖価格に関するデータなど、他の多くの一連のダイナミクスを置き換えたり、予測、検証、トレーニング期間を変更したり、他の外部要因を追加したり、適切な予測。言い換えれば、単純な自筆のシミュレーターが作業で使用され、その助けを借りて、さまざまな一連のダイナミクスを予測することができます。コードはここで見ることができます

記事の概要

シミュレータの簡単な説明。
正面からの解決策は、時系列の過去の値の「生の」データのみを使用して時系列を予測することです。
外因性変数の追加。
初期データの対数による不均一分散の修正。
行を静止したものにします。
単層ニューラルネットワークによる予測。
アプローチの比較。
便利なリンク

シミュレータの簡単な説明

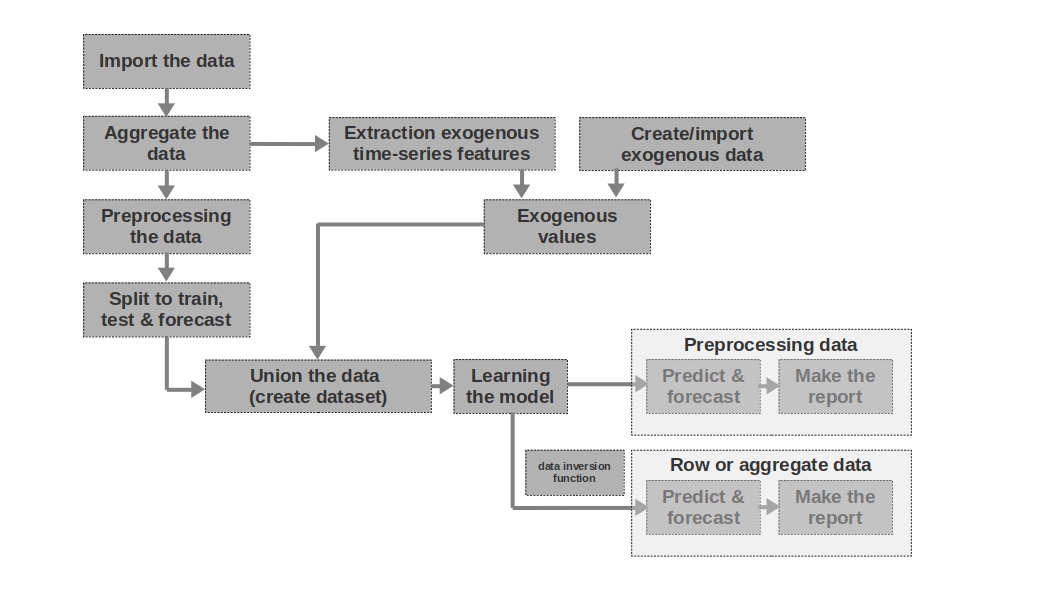
データのインポート

ここではすべてが簡単です。データをインポートします。生データで多かれ少なかれわかりやすい予測を作成するのに十分な場合があります。生データに基づいてモデル化されたのは、記事の1番目と2番目の予測です。つまり、過去の期間の賃金に関する生データを使用して賃金を予測します。

データを集約する

この記事では、データ集約は必要ないため、使用していません。ただし、データは多くの場合、不均等な時間間隔で表示される可能性があります。この場合、それらを集約する必要があります。たとえば、証券、通貨、その他の金融商品の取引からのデータを集計する必要があります。通常、間隔の平均値が取得されますが、最大、最小、標準偏差、およびその他の統計も可能です。

データの前処理この

場合、主にデータの前処理について説明します。これにより、時系列は等分散性のプロパティを取得し（データの対数を介して）、定常になります（系列の微分を介して）。

トレーニング、テスト、予測に分割

このコードブロックでは、時系列は、対応する値「train」、「test」、「forecast」を持つ新しい列を追加することにより、トレーニング、テスト、および予測の期間に分割されます。つまり、期間ごとに3つの個別のテーブルを作成するのではなく、列を追加するだけで、それに基づいてデータをさらに分割します。

外因性時系列特徴の抽出

時系列から追加の外部（外因性）特徴を分離すると便利な場合があります。たとえば、休日かどうか、1か月の日数（または1か月の稼働日数）などを示します。原則として、これらの記号は時系列から「引き出され」ます。手作業による介入なしでそれ自体。

外因性データの作成/インポート

時系列からすべての情報を「引き出す」ことができるわけではありません。追加の外部データが必要になる場合があります。たとえば、時系列の値に強い影響を与えるいくつかの一時的なイベント。そのような出来事は、敵対行為の開始日、制裁の賦課、自然災害などである可能性があります。作業はそのような要因を考慮していませんが、それらの使用の可能性を念頭に置く必要があります。

外因性の値

このコードブロックでは、すべての外因性データを1つのテーブルに結合します。

データ

を結合する（データセットを作成する）このコードブロックでは、時系列の値と外因性の特徴を1つのテーブルに結合します。つまり、データセットを準備しており、それに基づいてモデルをトレーニングし、品質をテストして、予測を作成します。

モデルの学習

ここではすべてが明確です。モデルをトレーニングしているだけです。

前処理データ：予測と予測

モデルのトレーニングに前処理データ（対数、ボックスコークス関数で処理、定常系列など）を使用した場合、モデルの品質は最初に前処理データでのみ評価されます。次に、「生の」データについて。データを前処理しなかった場合、この段階はスキップされます。

行データ：予測と予測

この段階は最後の段階です。たとえば、モデルが前処理されたデータでトレーニングされた場合、それらをプロローグし、ルーブルの対数ではなくルーブルの賃金の予測を取得するには、予測をルーブルに変換し直す必要があります。

また、この記事では、賃金を予測するために1次元の時系列を使用していることにも注意してください。ただし、ルーブルの為替レートに関するデータをドルやその他のシリーズに追加するなど、多次元シリーズを使用することを妨げるものは何もありません。

額の決定

過去の賃金に関するデータは、将来の賃金に近似できると想定します。言い換えれば、たとえば1月の賃金の大きさは、12月、11月、10月の賃金によって異なります...

過去12か月の賃金の値を使用して、13か月目の賃金を予測しましょう。つまり、ターゲット値ごとに12個の機能があります。

標識は、sklearnライブラリのリッジ回帰入力に送られます。モデルのデフォルトパラメータを使用しますが、アルファパラメータを除いて、0に設定されています。つまり、実際には、通常の回帰を使用しています。

これは簡単な解決策です-最も簡単です:)少なくともいくつかの結果を非常に緊急に与える必要がある状況がありますが、前処理の時間がないか、データを迅速に処理または追加するための十分な経験がありません。このような状況では、生データをベースラインとして使用して予測を作成できます。今後、モデルの品質は、データ前処理を使用するモデルの品質に匹敵することが判明したことに注意してください。

私たちが得たものを見てみましょう。

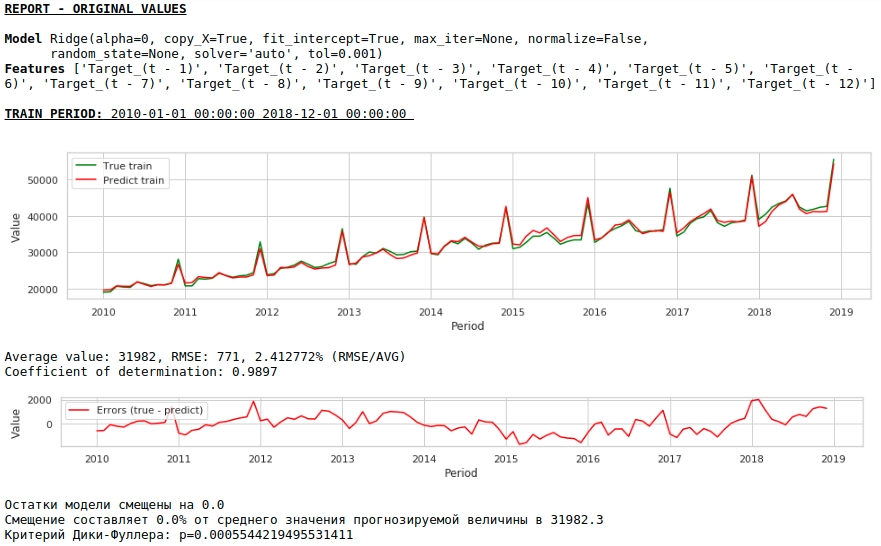
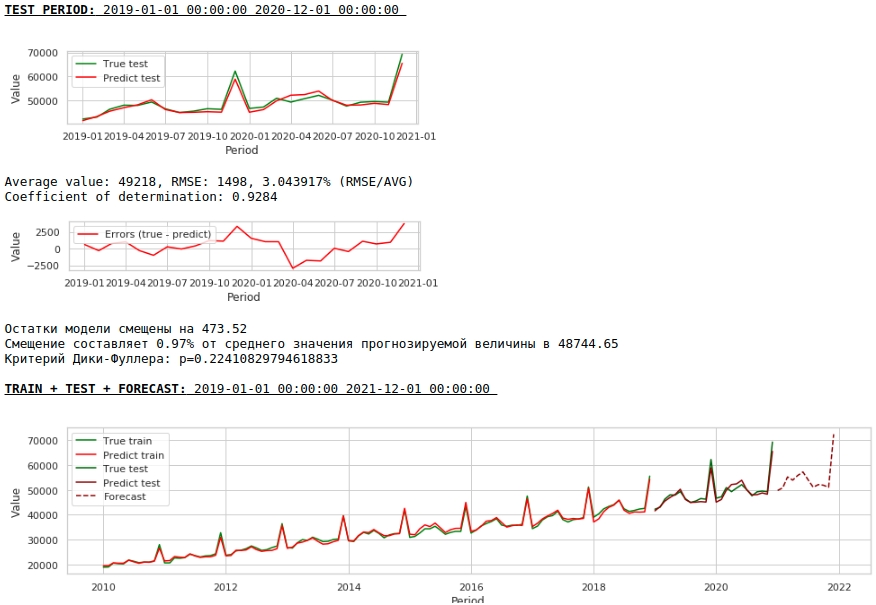
一見、結果は不完全ですが、現実に近いように見えます。

回帰係数の値によれば、給与の値はちょうど1年前の賃金の予測に最も大きな影響を及ぼします。

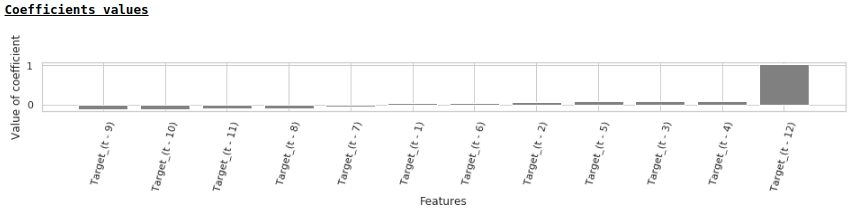
モデルに外因性変数を追加してみましょう。

外因性変数の追加

月の日数と月の数（1から12）の2つの外部記号を使用します。属性「Monthnumber」を2値化すると、月ごとに0または1の値を持つ12列が取得されます。

新しいデータセットを作成して、モデルの品質を見てみましょう。

チャートを見る

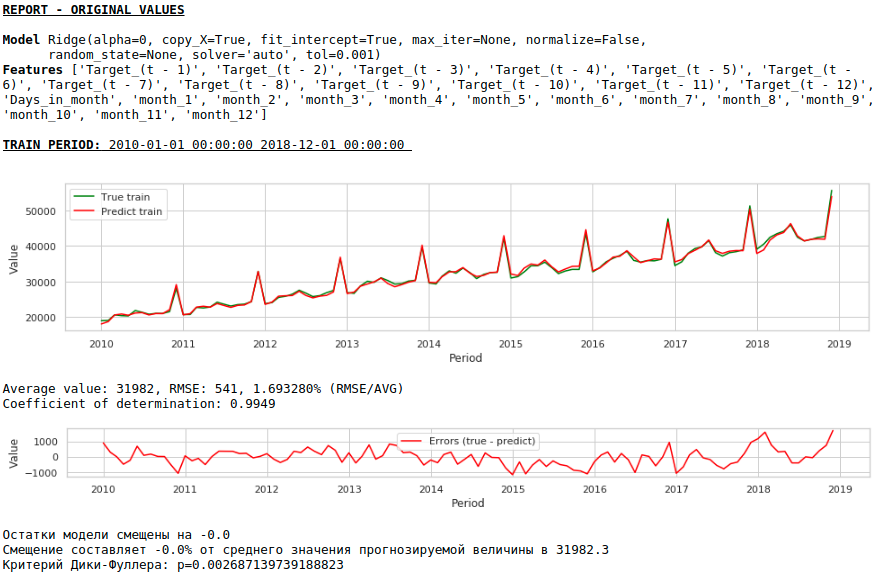
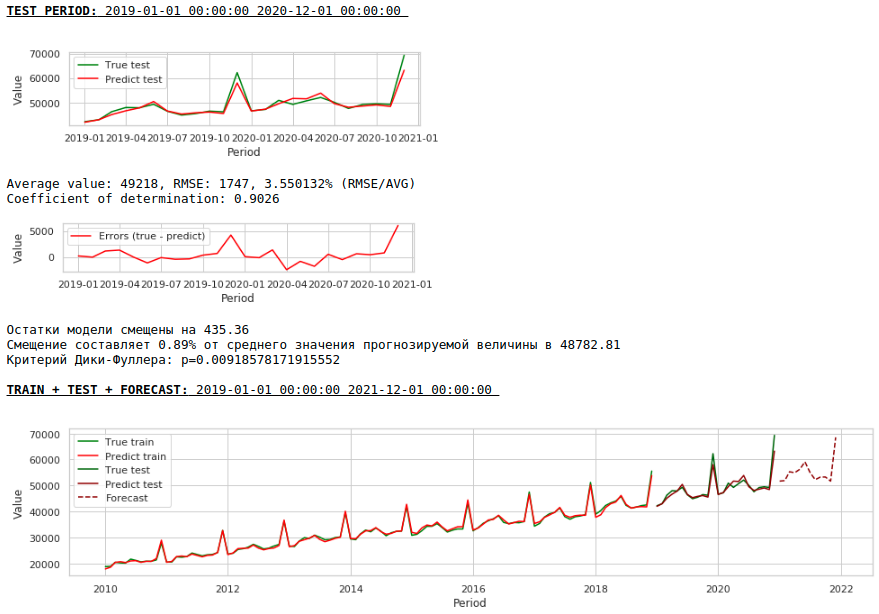
品質が低くなります。視覚的には、12月の賃金上昇に関して予測が完全に妥当であるようには見えないことが注目に値します。

それでは、最初のデータ前処理を行いましょう。

不均一分散の修正。

2010年から2020年までの賃金チャートを見ると、年内の月間賃金の広がりが年々増加していることがわかります。

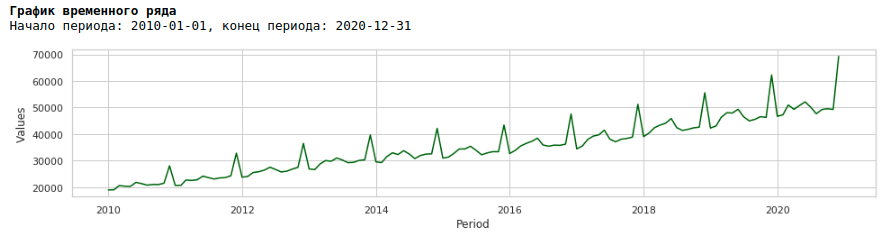
月ごとの分散の年次増加は、不均一分散につながります。予測の品質を向上させるには、データのこの特性を取り除き、等分散性にする必要があります。

これを行うには、通常の対数を使用して、対数級数がどのように見えるかを確認します。

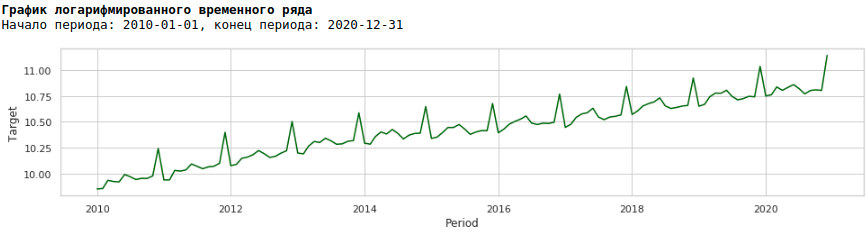
対数級数でモデルをトレーニングしましょう

チャートを見る

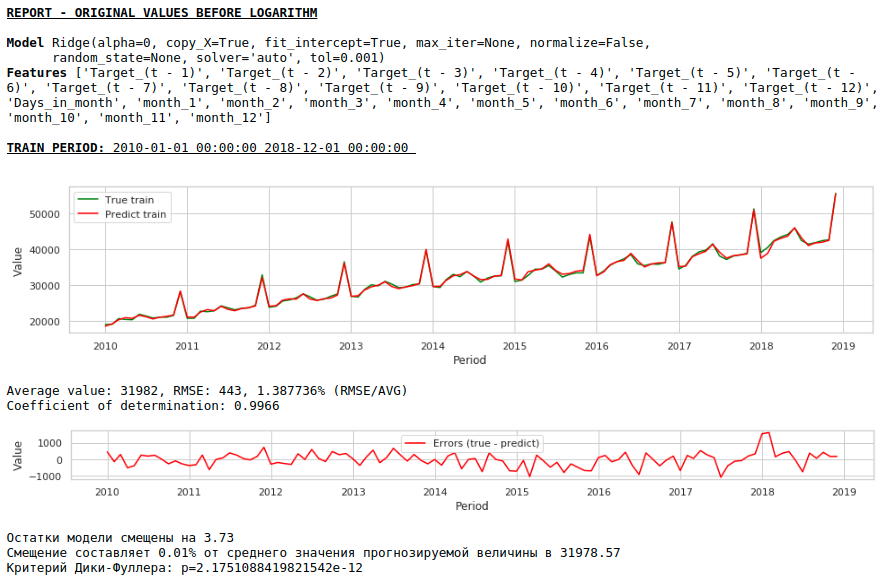
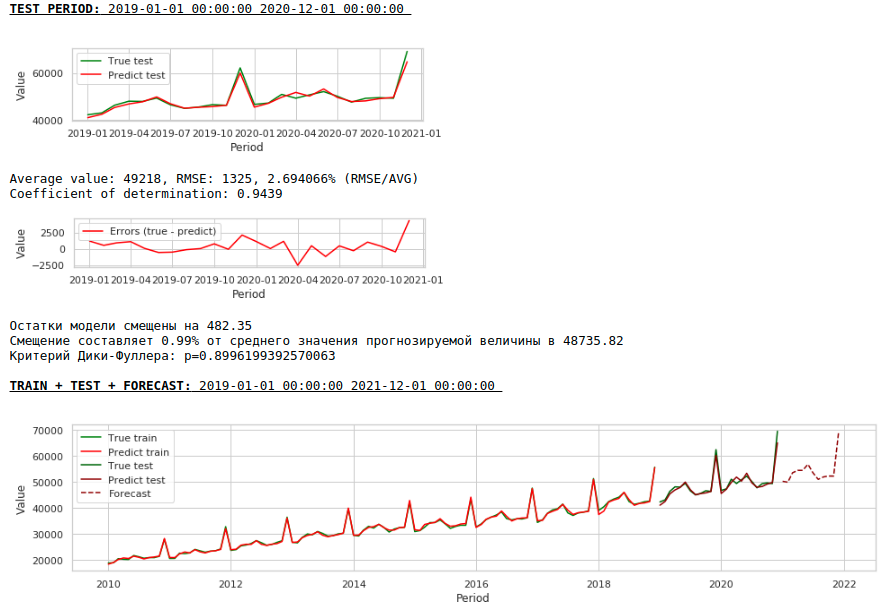
その結果、トレーニングサンプルとテストサンプルの予測の品質は向上しましたが、2021年の予測は、最初のモデルの予測と比較して視覚的に妥当性が低いように見えます。ほとんどの場合、外因性の要因を使用するとモデルが劣化します。

行を静止させる

次のように、シリーズを静止シリーズに減らします。

目標給与値と1年前の値の差を決定します。t-（t-12）= dif_1
受信した値とシフトした1か月の値の差を決定します：dif_1-（dif_1-1）= dif_2

その結果、次の時系列が得られます。

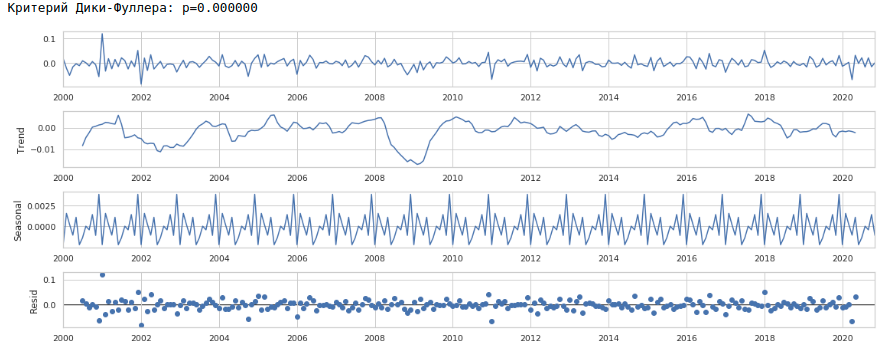
シリーズは実際には静止しているように見えます。これは、ディッキー-フラー基準の値によっても示されます。

実際、この場合、モデルはホワイトノイズの値を予測する必要があるため、処理されたデータ、つまり定常系列のトレーニングサンプルとテストサンプルで高品質の予測を期待する必要はありません。しかし、私たちにとって、賃金を予測するために回帰を使用する必要はまったくありません。なぜなら、級数を定常的なものに減らすことによって、簡単に言えば、ターゲット変数を近似するための式を決定したからです。しかし、私たちは規範から逸脱せず、回帰モデルを使用します。さらに、外因性の要因があります。

何が起きたのか見てみましょう。

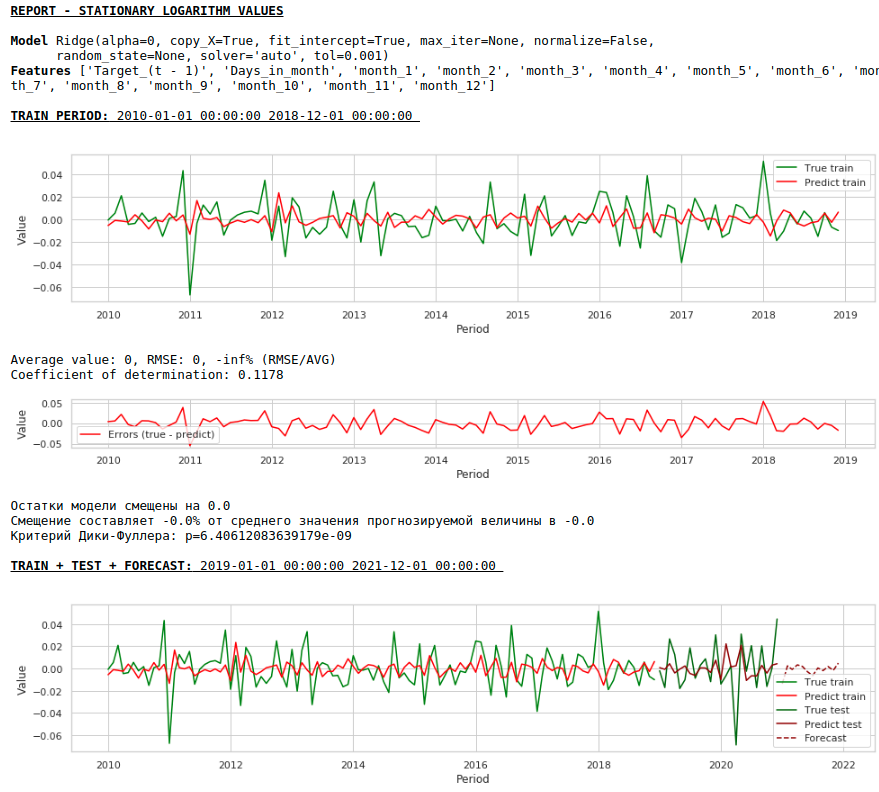
これは、定常系列の予測がどのように見えるかです。予想通り-あまり良くありません:)

そしてここに賃金の予測と予測があります。

チャートを見る

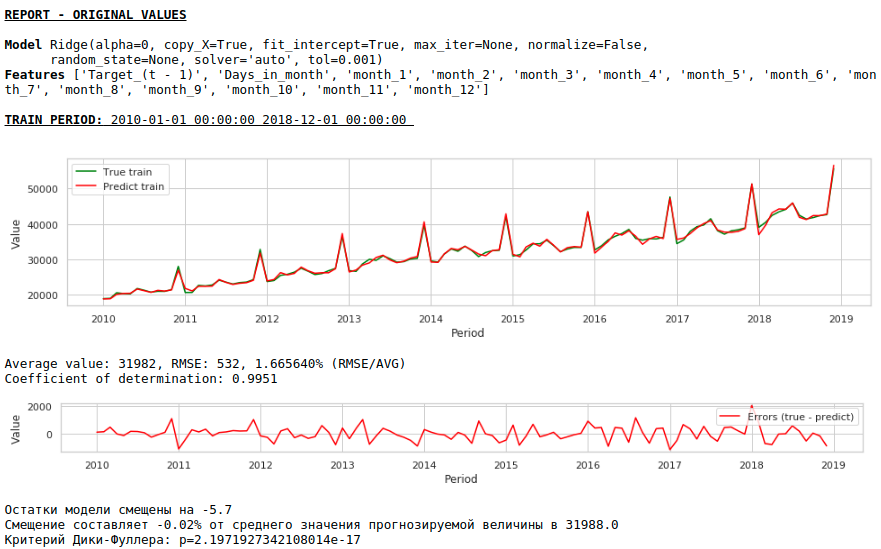
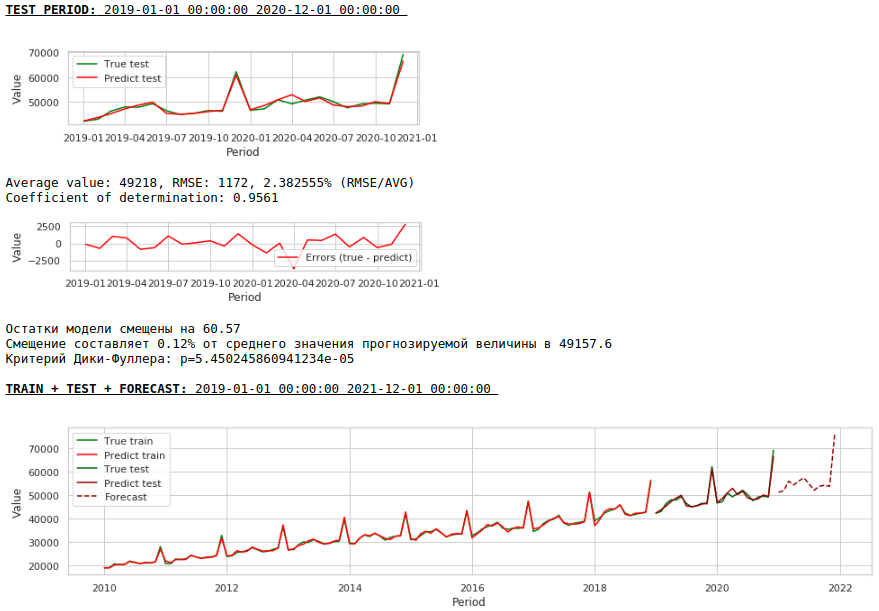
品質は著しく向上し、予測は視覚的に信頼できます。

それでは、外因性変数を使用せずに予測を作成しましょう。

チャートを見る

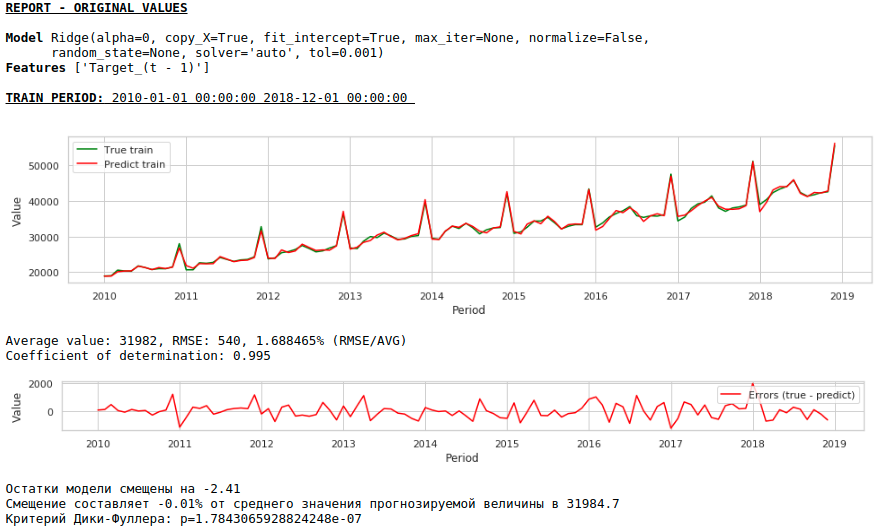
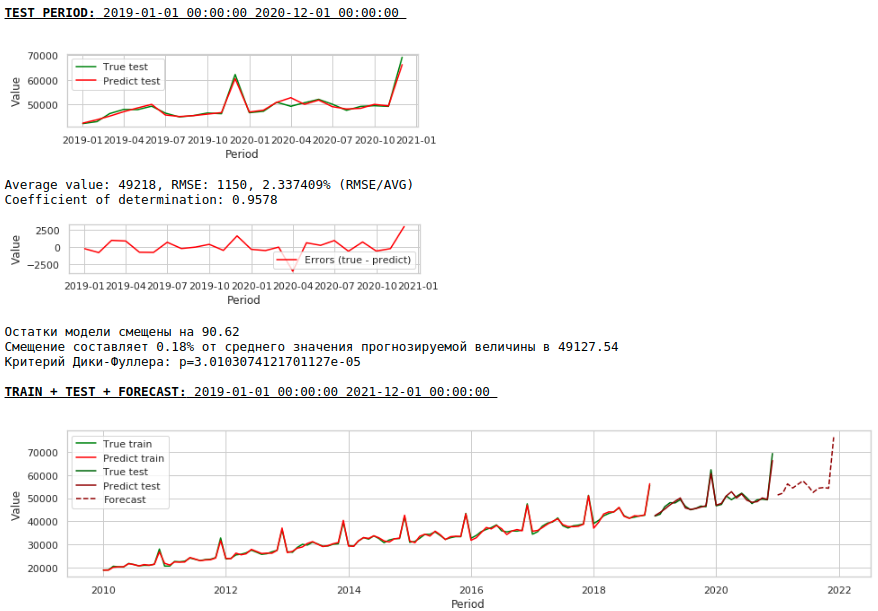
品質はさらに向上し、予測の妥当性は維持されます:)

単層ニューラルネットワークによる予測

既存のデータセットをニューラルネットワークの入力にフィードします。私たちのネットワークは単層であるため、実際、これは単純な変更を加えた同じ線形回帰であり、予測の品質に大きな違いは期待できません。

まず、ネットワーク自体を見てみましょう。

コードを見る

class Model_1(nn.Module):
    def __init__(self, input_size, output_size):
        super(Model_1, self).__init__()
        self.input_size = input_size
        self.output_size = output_size
        self.linear = nn.Linear(self.input_size, self.output_size)
        
    def forward(self, x):
        output = self.linear(x)
        return output

次に、彼女をどのように訓練するかについて少し説明します。

結果の再現性を目的として、ランダムシードを修正します
モデルの初期化
損失関数の設定-MSELoss
オプティマイザとしてAdamオプティマイザを選択する
トレーニングの最初のステップを示し、ステップが下げられる条件を決定します。ステップの正しい選択とそのさらなる変更（通常は減少）が良い結果をもたらすことに注意してください。
学習エポックの数を指定します
トレーニングを開始します
データセットは非常に小さく、バッチに分割しても意味がないため、データセット全体をネットワーク入力に提供します。
トレーニング中、1000エポックごとに、トレーニングサンプルとテストサンプルの損失関数の値のグラフを作成します。これにより、モデルの過剰適合または再トレーニングを制御できます。

以下は、最初のデータセットでネットワークをトレーニングするためのコードです。データセットごとに、パラメーターがわずかに変化しました。トレーニングエポックの数とトレーニングステップです。

コードを見る

# fix the random seed
SEED = 42
random_init(SEED)

# initialization model, loss function, optimizator
model = Model_1(len(features),1)
loss_func = nn.MSELoss()
opt = torch.optim.Adam(model.parameters(), lr=5e-2)

# set the epoch numbers, initialization list for every loss after learning on epoch
epochs = 15000
losses_train = []
losses_test = []
# initialization counter for calculation epoch numbers
counter = 0
# start the learning model
for epoch in range(epochs):
    model.train()
#     make prediction targets on train data
    y_pred_train = model(torch.tensor(X_train.to_numpy(), dtype=torch.float))
#     calculate loss
    loss = loss_func(y_pred_train, 
                     torch.reshape(torch.tensor(y_train.to_numpy(), dtype=torch.float),(-1,1)))
#     bacward loss to model and calculate new parameters (coefficients) with fixed learning rate
    loss.backward()
    opt.step()
    opt.zero_grad()

# add loss to list losses 
    losses_train.append(loss)
    
    model.eval()
    y_pred_test = model(torch.tensor(X_test.to_numpy(), dtype=torch.float))
    loss_test = loss_func(y_pred_test, 
                     torch.reshape(torch.tensor(y_test.to_numpy(), dtype=torch.float),(-1,1)))
    losses_test.append(loss_test)
    
    
# make the mini report for every 1000 epoch    
    if epoch % 1000 == 0 and epoch > 0:
        print ('Epoch:', epoch // 1000)
        print ('Learning rate:', opt.param_groups[0]['lr'])
        print ('Last loss on TRAIN data:', losses_train[-1].cpu().detach().numpy(),
              '              Last loss on TEST data:', losses_test[-1].cpu().detach().numpy())
#         print ('Last loss on TEST data:', losses_test[-1].cpu().detach().numpy())
        fig, (ax1, ax2) = plt.subplots(1, 2)
#         fig.suptitle('MSE on TRAIN & TEST DATA')
        fig.set_figheight(3)
        fig.set_figwidth(12)
        ax1.plot(np.arange(counter,epoch,1), np.array([float(i) for i in losses_train][-1000:]), color = 'darkred')
        plt.xlabel("Epoch")
        plt.ylabel("Loss on TRAIN data")
        ax2.plot(np.arange(counter,epoch,1), np.array([float(i) for i in losses_test][-1000:]), color = 'darkred')
        plt.xlabel("Epoch")
        plt.ylabel("Loss on TEST data")
        plt.show()
        
        counter += 1000
        
#   reduce learning rate
    if epoch == 1000:
        opt = torch.optim.Adam(model.parameters(), lr=7e-3)

各データセットの予測の品質を個別に検討することはありません（希望する人はギーターの詳細を見ることができます）。最終結果を比較してみましょう。

リッジ回帰を使用したテストサンプルの

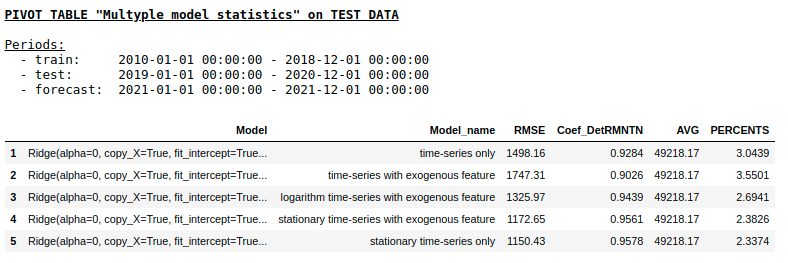
品質単層NNを使用したテストサンプルの品質

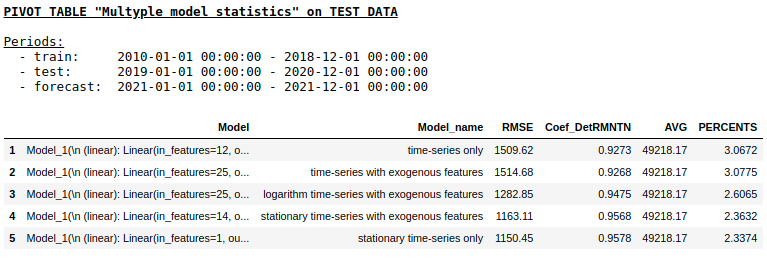
予想どおり、通常の回帰と単純な単層ニューラルネットワークの間に基本的な違いはありませんでした。もちろん、ニューロンは学習のためのより多くの操作を提供します。オプティマイザーの変更、学習ステップの調整、隠れ層と活性化関数の使用、さらに進んでリカレントニューラルネットワーク（RNN）の使用が可能です。ちなみに、個人的にはRNNを使ってこの問題でまともな品質を得ることができませんでしたが、インターネット上では、LSTMを使った時系列予測の興味深い例をたくさん見つけることができます。

この時点で、記事は終了しました。この資料が時系列の予測に使用されるベースラインアプローチの一種の概要として役立ち、MIPTとYandexの「データ分析の応用問題」コースへの実用的な追加として役立つことを願っています。

時系列。簡単な解決策

記事の概要

シミュレータの簡単な説明

額の決定

外因性変数の追加

不均一分散の修正。

行を静止させる

単層ニューラルネットワークによる予測

便利なリンク

More articles: