マハラノビス距離

コンテンツ

マハラノビスメトリックを使用する主な意味

1.用語と定義

2.2つのポイント間およびポイントとクラス間のマハラノビス距離

2.1。理論情報

2.2。2点間および点とクラス間の距離を計算するためのアルゴリズム

2.3。2点間および点とクラス

3間の距離の計算例。2つのクラス間のマハラノビス距離

3.1。理論情報

3.2。2つのクラス間の距離を計算するためのアルゴリズム

3.3。2つのクラス間の距離を計算する例

4.マハラノビス距離とk最近傍法

5.マハラノビスの加重距離

6.結論

コメントやエラーがある場合は、quwarm @ gmail.comまたはコメントに書き込んでください。

---

マハラノビス距離を使用する主なポイント

図1では、2つの観測値が赤い点で示されています。

クラスの中心は青い点で示されています。

問題は、どの観察がクラスの中心に近いかということです。

答えは、距離の測定方法によって異なります。

我々はに応じて距離を測定する場合は、ユークリッドメトリック、我々は、クラスの中心からの距離ことを得るポイントにはに等しくなる点まで、等しく、それはある、ポイントは近いクラスの中心に。

, , « » , .

, , , , . , , , , . . . — .

, , .

---

1.

— , , — .

— : , — .

— : .

, — .

«» - . .

-. - — , .

: .

, (-) .

2.

( ) ( ) .

2.1

— , ( ) :

, , .

, .

, ( 1) ( 0) , .

-.

( [internet archive] ), . . :

1. : ;

2. : ;

3. : .

: .

, 0, 0 (max(0.0, value)



) NaN, ( sqrt



0.5



) 0 (, ). .

, — .

( ) , — ( ) (. . « »).

, . , .

(, - , . 4) , .

, , * .

*

:

— , — , — .

:

— .

, ().

. , — , :

— — ( , . «sample covariance»):

— , — .

, . , ( , . «population covariance»):

:

1. () , ;

   
   
   
   
   

2. , ( ), ;

   
   
   
   
   

3. , ( *).

   
   
   
   
   

4. : .

   
   
   
   
   

5. — : .

   
   
   
   
   

*

— .

, :

— .

2.

, , ( ), , . .

, :

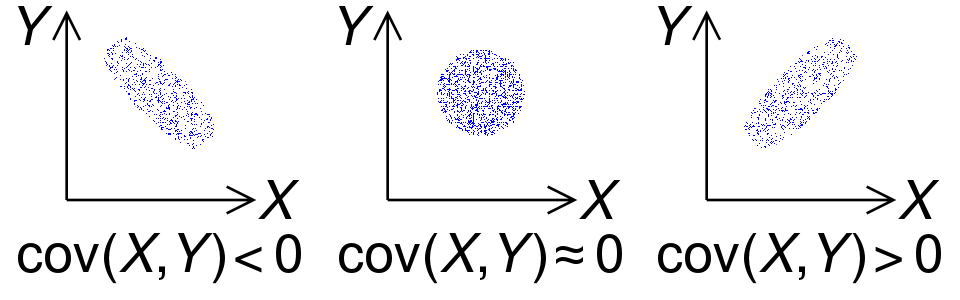
1. - , , .

: .

2. (, «perfect covariance»). :

— ;

— .

3. :



.

, ?

.

, .

:

1.

1. , ( — ) .

   
   
   
   
   

2. .

   
   
   
   
   

2. —

(, ), — - ( ):

— , .

, .

3.

.

— ( — ).

:

— ginv MASS (R);

— pinv numpy (Python);

— pinv MATLAB;

— pinv Octave.

, , ( ) , «» : , — , () (); , «» , «» .

. .

, ( , — ), : .

:

, : « . , , » ( ).

, , (- ).

4.

(shrinkage) — (. . ).

, — , — , , .

:

Olivier Ledoit Michael Wolf — , — , , — , .

, , Python scikit-learn (sklearn.covariance.LedoitWolf, sklearn.covariance.ledoit_wolf, sklearn.covariance.ledoit_wolf_shrinkage).

. 8 , « , , » ( ). — ( , , ) , .

.

, ( Python):

— ;

— : ;

— : ;

— : ;

— : .

:



— .

Shrunk Covariance (sklearn.covariance.ShrunkCovariance, sklearn.covariance.shrunk_covariance). , ( ).

( Ledoit — Wolf): .

.

, LedoitWolf ShrunkCovariance ( ) empirical_covariance, (. «population covariance», ).

5.

( ), « »:

— ( / ) ( , «corrected sample standard deviation»):

— / ) .

:

, . , ( , . «uncorrected sample standard deviation»):

- .

6.

:

:

- .

, .

, , 10 , . , , , .

2.2

1. .

2. .

3. .

4. , . , .

2.3

(. 3):

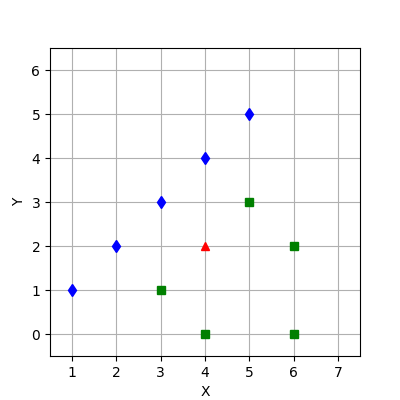
1. .

2. .

:

:

3. .

.

:

: . , .

.

:

: . , .

Python 3.6 numpy 1.19.5

import numpy as np

classes = [
    np.array([[1, 1], [2, 2], [3, 3], [4, 4], [5, 5]]),
    np.array([[3, 1], [4, 0], [6, 0], [6, 2], [5, 3]])
]

centroids = [class_.mean(axis=0) for class_ in classes]
standard_deviations = [class_.std(axis=0, ddof=1) for class_ in classes]
covariance_matrices = np.array([np.cov(class_, rowvar=False, ddof=1) for class_ in classes])
det_covariance_matrices = [np.linalg.det(cov) for cov in covariance_matrices]

print("Centroids:", *centroids)
print("Standard deviations:", *standard_deviations)
print("Covariance matrices:", *covariance_matrices.tolist())
print("Determinants of covariance matrices:", det_covariance_matrices)

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

Centroids: [3. 3.] [4.8 1.2]
Standard deviations: [1.58113883 1.58113883] [1.30384048 1.30384048]
Covariance matrices: [[2.5, 2.5], [2.5, 2.5]] [[1.7, 0.3], [0.3, 1.7]]
Determinants of covariance matrices: [0.0, 2.8]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

4. , — . , .

, , , .

, .

. — , 5 : (1) — , (2) (LedoitWolf), (3) , (4) , (5) — :

1. — .

Python 3.6 numpy 1.19.5

import numpy as np


def mahalanobis(point_from, point_to, inverse_covariance_matrix):
    delta = point_from - point_to
    return max(np.float64(0), np.dot(np.dot(delta, inverse_covariance_matrix), delta)) ** 0.5


test_point = np.array([4., 2.])
class_ = np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]])
covariance_matrix = np.cov(class_, rowvar=False, ddof=1)
inverse_covariance_matrix = np.linalg.inv(covariance_matrix + np.identity(covariance_matrix.shape[0]))
print("  :\n", inverse_covariance_matrix, sep='')

for point_to in [class_.mean(axis=0), *class_]:
    print("d_E-M (", test_point, ", ", point_to, ", (COV+E)^(-1)) = ",
          mahalanobis(test_point, point_to, inverse_covariance_matrix), sep='')

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

  :
[[ 0.58333333 -0.41666667]
 [-0.41666667  0.58333333]]
d_E-M ([4. 2.], [3. 3.], (COV+E)^(-1)) = 1.414213562373095
d_E-M ([4. 2.], [1. 1.], (COV+E)^(-1)) = 1.8257418583505538
d_E-M ([4. 2.], [2. 2.], (COV+E)^(-1)) = 1.5275252316519465
d_E-M ([4. 2.], [3. 3.], (COV+E)^(-1)) = 1.414213562373095
d_E-M ([4. 2.], [4. 4.], (COV+E)^(-1)) = 1.5275252316519465
d_E-M ([4. 2.], [5. 5.], (COV+E)^(-1)) = 1.8257418583505536
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

— , .

2. (LedoitWolf).

Python 3.6 numpy 1.19.5 scikit-learn 0.24.1

import numpy as np
from sklearn.covariance import LedoitWolf


def mahalanobis(point_from, point_to, inverse_covariance_matrix):
    delta = point_from - point_to
    return max(np.float64(0), np.dot(np.dot(delta, inverse_covariance_matrix), delta)) ** 0.5


def approx(number, *, sign, epsilon=1e-4):
    return number + np.sign(sign) * epsilon


test_point = np.array([4., 2.])
class_ = np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]])
lw = LedoitWolf().fit(class_)
lw_covariance_matrix = lw.covariance_
lw_lambda = lw.shrinkage_
covariance_matrix = np.cov(class_, rowvar=False, ddof=0)
mu = np.sum(np.trace(covariance_matrix)) / class_.shape[0]
T = mu * np.identity(class_.shape[1])
print("T:", *T)
print("COV(*):", *lw_covariance_matrix)
print("Lambda:", lw_lambda)

#   - T    
# ( :     T )
# ddof=0, . . LedoitWolf  empirical_covariance (.  )
first_condition = (np.linalg.eig(T)[0] > approx(0., sign=+1)).all()
print("All(", np.linalg.eig(T)[0], ") > 0 ? -> ", first_condition, sep='')

#   -    (0, 1]
second_condition = approx(0., sign=+1) < lw_lambda <= 1
print("Lambda =", lw_lambda, "in (0, 1] ? ->", second_condition)

#   -     COV(*)
#     lambda,      T
cov_eig = min(np.linalg.eig(lw_covariance_matrix)[0])
lambda_t_eig = lw_lambda * min(np.linalg.eig(T)[0])
third_condition = cov_eig >= lambda_t_eig
print(cov_eig, ">=", lambda_t_eig, "? ->", third_condition)
conditions = [first_condition, second_condition, third_condition]

if all(conditions):
    print("   ")
    #  
    inverse_lw_covariance_matrix = np.linalg.inv(lw_covariance_matrix)
    print("  :\n", inverse_lw_covariance_matrix, sep='')
    for point_to in [class_.mean(axis=0), *class_]:
        print("d_M(*) (", test_point, ", ", point_to, ", COV(*)) = ",
              mahalanobis(test_point, point_to, inverse_lw_covariance_matrix), sep='')
else:
    print("  (1-3): ", [i for i, x in enumerate(conditions, 1) if not x])

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

T: [0.8 0. ] [0.  0.8]
COV(*): [2.   1.44] [1.44 2.  ]
Lambda: 0.27999999999999997
All([0.8 0.8]) > 0 ? -> True
Lambda = 0.27999999999999997 in (0, 1] ? -> True
0.56 >= 0.22399999999999998 ? -> True
   
  :
[[ 1.03820598 -0.74750831]
 [-0.74750831  1.03820598]]
d_M(*) ([4. 2.], [3. 3.], COV(*)) = 1.889822365046136
d_M(*) ([4. 2.], [1. 1.], COV(*)) = 2.4283759936997833
d_M(*) ([4. 2.], [2. 2.], COV(*)) = 2.037847864848056
d_M(*) ([4. 2.], [3. 3.], COV(*)) = 1.889822365046136
d_M(*) ([4. 2.], [4. 4.], COV(*)) = 2.037847864848056
d_M(*) ([4. 2.], [5. 5.], COV(*)) = 2.4283759936997833
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

— , .

3. .

. .

, — .

Python 3.6 numpy 1.19.5

import numpy as np


def mahalanobis(point_from, point_to, inverse_covariance_matrix):
    delta = point_from - point_to
    return max(np.float64(0), np.dot(np.dot(delta, inverse_covariance_matrix), delta)) ** 0.5


test_point = np.array([4., 2.])
class_ = np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]])
covariance_matrix = np.cov(class_, rowvar=False, ddof=1)
#    (Singular Value Decomposition, SVD)
#    
pseudo_inverse_covariance_matrix = np.linalg.pinv(covariance_matrix)
print("  :\n", pseudo_inverse_covariance_matrix, sep='')

for point_to in [class_.mean(axis=0), *class_]:
    print("d_M+ (", test_point, ", ", point_to, ", COV+) = ",
          mahalanobis(test_point, point_to, pseudo_inverse_covariance_matrix), sep='')

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

  :
[[0.1 0.1]
 [0.1 0.1]]
d_M+ ([4. 2.], [3. 3.], COV+) = 0.0
d_M+ ([4. 2.], [1. 1.], COV+) = 1.2649110640673513
d_M+ ([4. 2.], [2. 2.], COV+) = 0.6324555320336757
d_M+ ([4. 2.], [3. 3.], COV+) = 0.0
d_M+ ([4. 2.], [4. 4.], COV+) = 0.6324555320336757
d_M+ ([4. 2.], [5. 5.], COV+) = 1.2649110640673513
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

— , .

4. .

Python 3.6 numpy 1.19.5

import numpy as np


def euclid_std(point_from, point_to, standard_deviations):
    return sum(((point_from - point_to) / standard_deviations) ** 2) ** 0.5


def approx(number, *, sign, epsilon=1e-4):
    return number + np.sign(sign) * epsilon


test_point = np.array([4., 2.])
class_ = np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]])
standard_deviations = class_.std(axis=0, ddof=1)

#       0
std_le_0 = standard_deviations <= approx(0., sign=+1, epsilon=1e-6)
print(" :\n", standard_deviations, sep='')

if std_le_0.any():
    print("     0: ", np.where(std_le_0)[0])
else:
    for point_to in [class_.mean(axis=0), *class_]:
        print("d_std (", test_point, ", ", point_to, ", sigma) = ",
              euclid_std(test_point, point_to, standard_deviations), sep='')

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

 :
[1.58113883 1.58113883]
d_std ([4. 2.], [3. 3.], sigma) = 0.8944271909999159
d_std ([4. 2.], [1. 1.], sigma) = 1.9999999999999998
d_std ([4. 2.], [2. 2.], sigma) = 1.2649110640673518
d_std ([4. 2.], [3. 3.], sigma) = 0.8944271909999159
d_std ([4. 2.], [4. 4.], sigma) = 1.2649110640673518
d_std ([4. 2.], [5. 5.], sigma) = 1.9999999999999998
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

— , .

5. .

Python 3.6 numpy 1.19.5

import numpy as np


def euclid_std(point_from, point_to, standard_deviations):
    return sum(((point_from - point_to) / standard_deviations) ** 2) ** 0.5


def euclid_diag(point_from, point_to, standard_deviations):
    return euclid_std(point_from, point_to, standard_deviations) \
           * (np.prod(standard_deviations ** 2)) ** (1. / point_from.shape[0])


def approx(number, *, sign, epsilon=1e-4):
    return number + np.sign(sign) * epsilon


test_point = np.array([4., 2.])
class_ = np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]])
standard_deviations = class_.std(axis=0, ddof=1)

#       0
std_le_0 = standard_deviations <= approx(0., sign=+1, epsilon=1e-6)
print(" :\n", standard_deviations, sep='')

if std_le_0.any():
    print("     0: ", np.where(std_le_0)[0])
else:
    for point_to in [class_.mean(axis=0), *class_]:
        print("d_diag (", test_point, ", ", point_to, ", sigma) = ",
              euclid_diag(test_point, point_to, standard_deviations), sep='')

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

 :
[1.58113883 1.58113883]
d_diag ([4. 2.], [3. 3.], sigma) = 2.2360679774997902
d_diag ([4. 2.], [1. 1.], sigma) = 5.0
d_diag ([4. 2.], [2. 2.], sigma) = 3.16227766016838
d_diag ([4. 2.], [3. 3.], sigma) = 2.2360679774997902
d_diag ([4. 2.], [4. 4.], sigma) = 3.16227766016838
d_diag ([4. 2.], [5. 5.], sigma) = 5.0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

— , .

. ( ). :

— , — .

Python 3.6 numpy 1.19.5

import numpy as np


def mahalanobis(point_from, point_to, inverse_covariance_matrix):
    delta = point_from - point_to
    return max(np.float64(0), np.dot(np.dot(delta, inverse_covariance_matrix), delta)) ** 0.5


def approx(number, *, sign, epsilon=1e-4):
    return number + np.sign(sign) * epsilon


test_point = np.array([4., 2.])
class_ = np.array([[3., 1.], [4., 0.], [6., 0.], [6., 2.], [5., 3.]])
covariance_matrix = np.cov(class_, rowvar=False, ddof=1)
if abs(np.linalg.det(covariance_matrix)) <= approx(0., sign=+1):
    print("  0.  .")
else:
    inverse_covariance_matrix = np.linalg.inv(covariance_matrix)
    print("   (d_M):\n", inverse_covariance_matrix, sep='')
    for point_to in [class_.mean(axis=0), *class_]:
        print("d_M (", test_point, ", ", point_to, ", COV^(-1)) = ",
              mahalanobis(test_point, point_to, inverse_covariance_matrix), sep='')

covariance_matrix = covariance_matrix + np.identity(class_.shape[1])
inverse_covariance_matrix = np.linalg.inv(covariance_matrix)
print("   (d_E-M):\n", inverse_covariance_matrix, sep='')

for point_to in [class_.mean(axis=0), *class_]:
    print("d_E-M (", test_point, ", ", point_to, ", (COV+E)^(-1)) = ",
          mahalanobis(test_point, point_to, inverse_covariance_matrix), sep='')

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

   (d_M):
[[ 0.60714286 -0.10714286]
 [-0.10714286  0.60714286]]
d_M ([4. 2.], [4.8 1.2], COV^(-1)) = 0.9561828874675149
d_M ([4. 2.], [3. 1.], COV^(-1)) = 1.0
d_M ([4. 2.], [4. 0.], COV^(-1)) = 1.5583874449479593
d_M ([4. 2.], [6. 0.], COV^(-1)) = 2.3904572186687876
d_M ([4. 2.], [6. 2.], COV^(-1)) = 1.5583874449479593
d_M ([4. 2.], [5. 3.], COV^(-1)) = 1.0
   (d_E-M):
[[ 0.375      -0.04166667]
 [-0.04166667  0.375     ]]
d_E-M ([4. 2.], [4.8 1.2], (COV+E)^(-1)) = 0.7302967433402214
d_E-M ([4. 2.], [3. 1.], (COV+E)^(-1)) = 0.8164965809277259
d_E-M ([4. 2.], [4. 0.], (COV+E)^(-1)) = 1.224744871391589
d_E-M ([4. 2.], [6. 0.], (COV+E)^(-1)) = 1.8257418583505536
d_E-M ([4. 2.], [6. 2.], (COV+E)^(-1)) = 1.224744871391589
d_E-M ([4. 2.], [5. 3.], (COV+E)^(-1)) = 0.8164965809277259
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

— .

•

:

1. — : ;

2. (LedoitWolf): ;

3. : ;

4. : ;

5. : .

( ): .

( — ): .

3, ( ) — , .

•

:

1. — : ;

2. (LedoitWolf): ;

3. : ;

4. : ;

5. : .

( ): .

( — ): .

3, ( ) .

•

:

1. — : ;

2. (LedoitWolf): ;

3. : ;

4. : ;

5. : .

( ): .

( — ): .

3, ( ) — , .

.

3.

( ) .

, . .:

— , , .

— ( ) .

.

3.1

— :

— , — , — , — .

:

.

, , .

, , ( ) (. 2 « »):

- :

— , .

3.2

1. .

2. .

3. , .

4. , . , — .

3.3

. 2.2.

.

3 . 2.2.

4 .

4. , . , — .

:

:

•

.

— .

:

— ;

— — .

•

.

— .

:

— ;

— — .

•

.

— .

:

— ;

— — .

Python 3.6 numpy 1.19.5 .

4. k-

- . , - ( ) .

- .

:

— : ( — );

— ( , ).

Python 3.6 numpy 1.19.5

#    

import heapq
from collections import Counter
from operator import itemgetter

import numpy as np


class MkNN:
    def __init__(self, k, classes, inv_cov_matrices):
        self.n = len(classes)
        self.k = k
        self.classes = classes
        self.inv_cov_matrices = inv_cov_matrices

    @staticmethod
    def mahalanobis_sqr(point_from, point_to, inverse_covariance_matrix):
        delta = point_from - point_to
        return max(np.float64(0), np.dot(np.dot(delta, inverse_covariance_matrix), delta))

    def _get_k_smallest(self, test_point):
        generator = (
            (MkNN.mahalanobis_sqr(test_point, point, inv_cov), i)
            for i, (class_, inv_cov) in enumerate(zip(self.classes, self.inv_cov_matrices))
            for point in class_
        )
        return heapq.nsmallest(self.k, generator, key=itemgetter(0))

    def predict(self, test_point):
        return heapq.nlargest(1, Counter((i for _, i in self._get_k_smallest(test_point))).items(),
                              key=lambda t: (t[1], -t[0]))[0][0]

    def predict_proba(self, test_point):
        most_common = Counter((i for _, i in self._get_k_smallest(test_point)))
        classes_proba = np.array([most_common.get(i, 0) for i in range(self.n)])
        return classes_proba / classes_proba.sum()

    def predict_all_max(self, test_point):
        p = self.predict_proba(test_point)
        return np.where(p == max(p))[0]


def main():
    #  ,     -  classes
    test_points = np.array([[4., 2.]])
    #   
    classes = [
        np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]]),
        np.array([[3., 1.], [4., 0.], [6., 0.], [6., 2.], [5., 3.]])
    ]
    #   
    n_train_points = sum(class_.shape[0] for class_ in classes)
    #      
    cov_matrices = [np.cov(class_, rowvar=False, ddof=1) for class_ in classes]
    #        --   - 
    inv_cov_matrices = [np.linalg.inv(cov + np.identity(cov.shape[0])) for cov in cov_matrices]
    for test_point in test_points:
        print("Point:", test_point)
        # k  1    ( )
        for i in range(1, n_train_points):
            classifier = MkNN(i, classes, inv_cov_matrices)
            print(f"{i}nn:",
                  1 + classifier.predict(test_point),
                  classifier.predict_proba(test_point),
                  classifier.predict_all_max(test_point))


if __name__ == "__main__":
    main()

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

"knn: [ ( 1), ] [ ] [ ( 0), ]".

Point: [4. 2.]
1nn: 2 [0. 1.] [1]
2nn: 2 [0. 1.] [1]
3nn: 2 [0. 1.] [1]
4nn: 2 [0. 1.] [1]
5nn: 2 [0.2 0.8] [1]
6nn: 2 [0.33333333 0.66666667] [1]
7nn: 2 [0.42857143 0.57142857] [1]
8nn: 1 [0.5 0.5] [0 1]
9nn: 2 [0.44444444 0.55555556] [1]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

. 4.

Python 3.6

# ...

from operator import sub

import numpy as np  # 1.19.5
from matplotlib import colors, pyplot as plt  # 3.3.4

#    
def show_data_on_mesh(k, classes, inv_cov_matrices):
    #  
    min_ = np.min([np.min(class_, axis=0) for class_ in classes], axis=1) - 1
    max_ = np.max([np.max(class_, axis=0) for class_ in classes], axis=1) + 1
    min_c = min(min_[0], min_[1])
    max_c = max(max_[0], max_[1])
    h = 0.05
    test_mesh = np.meshgrid(np.arange(min_c, max_c, h), np.arange(min_c, max_c, h))
    test_points = np.c_[test_mesh[0].ravel(), test_mesh[1].ravel()]
    #   
    classifier = MkNN(k, classes, inv_cov_matrices)
    test_mesh_labels = [sub(*classifier.predict_proba(x)) for x in test_points]
    #  
    plt.figure(figsize=(6, 5), dpi=90)
    class_colormap = colors.ListedColormap(['#070648', '#480607'])
    plt.pcolormesh(test_mesh[0], test_mesh[1],
                   np.asarray(test_mesh_labels).reshape(test_mesh[0].shape),
                   cmap='coolwarm', shading='nearest')
    plt.colorbar()
    plt.scatter([point[0] for class_ in classes for point in class_],
                [point[1] for class_ in classes for point in class_],
                c=[-i for i, class_ in enumerate(classes) for _ in class_],
                cmap=class_colormap)
    plt.axis([min_c, max_c, min_c, max_c])
    plt.xlabel("X")
    plt.ylabel("Y")
    plt.title("k=" + str(k))
    plt.show()

# ...

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

— .

5.

, — , :

( , ) :

— :

6.

, ( ) , - — .

?

1. , .

2. «Metric Learning» (: Aurélien Bellet, Amaury Habrard, Marc Sebban; ).

3. (, k-means: 1, 2, 3).

4. ().

5. ( 1, 記事2、記事3）。

---

コメントやエラーがある場合は、quwarm @ gmail.comまたはコメントに書き込んでください。