初心者向けの投稿#3は 、比較分析のための分布、それらのプロパティ、およびグラフの生成に専念しています。
ベイカーとポアンカレ
伝説、ほぼ確実に外典があり、中心極限定理が統計的分布の形成の原理についてどのように推論できるかという問題をより詳細に検討することを可能にします。それは有名な19世紀のフランスの博学者、アンリポアンカレに関係しています。アンリポアンカレは、伝説によれば、焼きたてのパンの重さを毎日1年間過ごしました。
当時、ベーキングは州によって規制されており、ポアンカレは、パンの塊を計量した結果は正規分布に従っているものの、ピークは公に宣伝されている1 kgではなく、950gであることを発見しました。彼が定期的にパンを買ったパン屋。そして彼は罰金を科された。これは伝説です;-)。
翌年、ポアンカレは同じパン屋からのパンの塊の計量を続けました。彼は、平均が1 kgになったことを発見しましたが、その分布はもはや平均の周りで対称ではありませんでした。右にシフトしました。これは、パン屋がポアンカレに彼のパンの中で最も重いものだけを与えていたという事実と一致していました。ポアンカレは再びパン屋を当局に報告し、パン屋は2度目の罰金を科されました。
それが本当にあったかどうかはここでは重要ではありません。この例は、重要なポイントを説明するのに役立ちます。一連の数値の統計的分布は、それを作成したプロセスについて重要なことを教えてくれます。
ディストリビューションの生成
正規分布と分散の直感的な理解を深めるために、正直で不正直なパン屋をシミュレートしましょう。このために、正規分布の確率変数stats.norm.rvsを生成する関数を使用します。(英語の正規変量、つまり確率変数からのrv)。公正なパン屋は、平均1000の正規分布としてモデル化できます。これは、公正な1kgのパンに相当します。そうすることで、30gの標準偏差につながるベーキングプロセスの変動の存在を許可します。
def honest_baker(mu, sigma):
''' '''
return pd.Series( stats.norm.rvs(loc, scale, size=10000) )
def ex_1_18():
''' '''
honest_baker(1000, 30).hist(bins=25)
plt.xlabel(' ')
plt.ylabel('')
plt.show()
上記の例では、次のようなヒストグラムがプロットされます。

, . ( « ») :
def dishonest_baker(mu, sigma):
''' '''
xs = stats.norm.rvs(loc, scale, size=10000)
return pd.Series( map(max, bootstrap(xs, 13)) )
def ex_1_19():
''' '''
dishonest_baker(950, 30).hist(bins=25)
plt.xlabel(' ')
plt.ylabel('')
plt.show()
, :
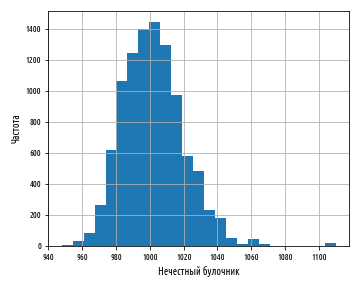
, , , . - 1 , . , .
. , , , . , , , .
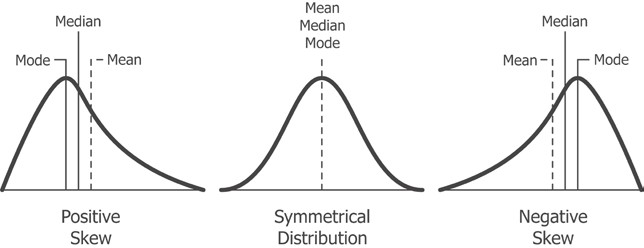
pandas skew
:
def ex_1_20():
''' '''
s = dishonest_baker(950, 30)
return { '' : s.mean(),
'' : s.median(),
'': s.skew() }
{'': 0.4202176889083849,
'': 998.7670301469957,
'': 1000.059263920949}
, 0.4. , .
. , quantile
0 1 . 0.5- .
, . , -, Q-Q, . Q-Q plot. . , , . , .
. qqplot
, :
def qqplot( xs ):
''' ( -, Q-Q plot)'''
d = {0:sorted(stats.norm.rvs(loc=0, scale=1, size=len(xs))),
1:sorted(xs)}
pd.DataFrame(d).plot.scatter(0, 1, s=5, grid=True)
df.plot.scatter(0, 1, s=5, grid=True)
plt.xlabel(' ')
plt.ylabel(' ')
plt.title (' ', fontweight='semibold')
def ex_1_21():
'''
'''
qqplot( honest_baker(1000, 30) )
plt.show()
qqplot( dishonest_baker(950, 30) )
plt.show()
:

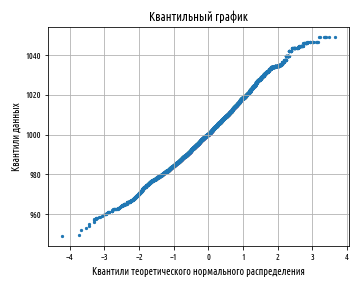
. :
, , , ; . , :

: , , , , ,
. ( ) .
() . , . , , .
, « », — , . :
def ex_1_22():
'''
'''
d = {' ' :honest_baker(1000, 30),
' ':dishonest_baker(950, 30)}
pd.DataFrame(d).boxplot(sym='o', whis=1.95, showmeans=True)
plt.ylabel(' (.)')
plt.show()
:

. — . — . , , . , .
. . , .
(), , . Cumulative Distribution Function (CDF), , , , x. , 0 1, 0 — , 1 — . , , . , 6?
5/6. , , , 1/6. — 50%.
, — , . , , , .
— . 0.5- 1000, 1000 0.5.
, pandas quantile
, empirical_cdf
0 1. , .. ( ) , , , , .
— , .
. pandas plot
, — — , . plot
, x y . pandas DataFrame
.
, plot
. pandas , . plot
, (ax
) plot
, (ax=ax
). . , . , (tp[1]
tp[3]
) , :
def empirical_cdf(x):
''' x'''
sx = sorted(x)
return pd.DataFrame( {0: sx, 1:sp.arange(len(sx))/len(sx)} )
def ex_1_23():
'''
'''
df = empirical_cdf(honest_baker(1000, 30))
df2 = empirical_cdf(dishonest_baker(950, 30))
ax = df.plot(0, 1, label=' ')
df2.plot(0, 1, label=' ', grid=True, ax=ax)
plt.xlabel(' ')
plt.ylabel('')
plt.legend(loc='best')
plt.show()
:
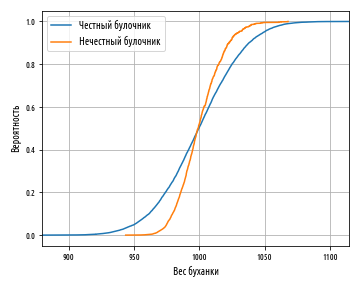
, -, , . , 0.5, 1000 . , .
, 4, «Python, » .