手元に電卓がなく(ただし、コンパスと定規または正方形がある)、結果を線分として計算する必要があるとします。この問題は、5つ未満の簡単な手順で解決されます。
基本計算式
まず、さらなる解決策に役立つ1つの公式を証明します。
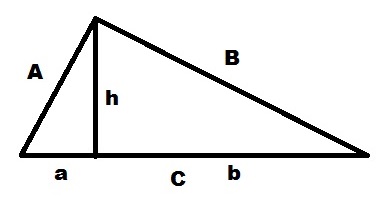
直角三角形でABC
、高さh
を横に描きC
ます。ピタゴラスの定理により、次のように推測します。
最初の式のすべてを置き換えます。
また、角かっこを展開すると、次のようになります。
削減後、次のようになります。
.
, 1
. 1
, 10
, 100
4
. 4 . , - . - , .
:
, .
.
. , 4 .
X
:
.

.

1
X
.
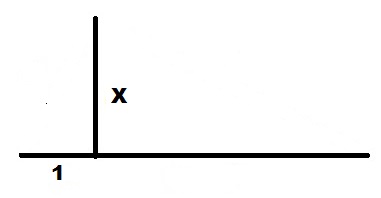
1
X
.
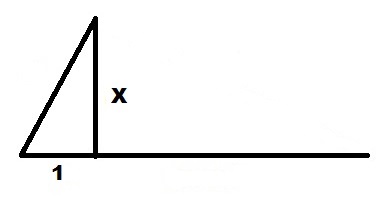
1
. . , .
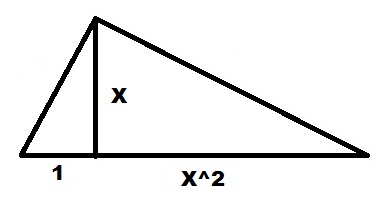
. - , X
, . . X
. ( 1
). , , .
:
.

1.

X
.
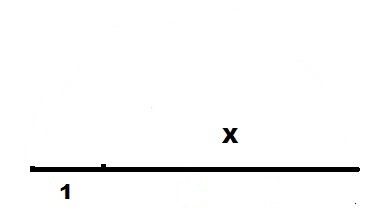
1+X
O
. , , . R
.
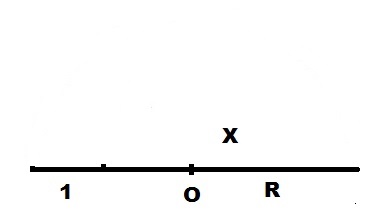
O
, R
.
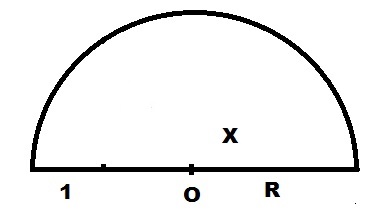
1 . X
.
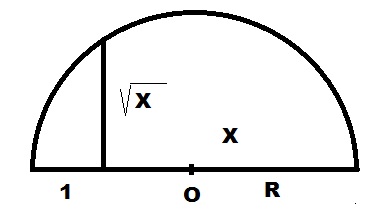
:
, a
h
.
.

X
.
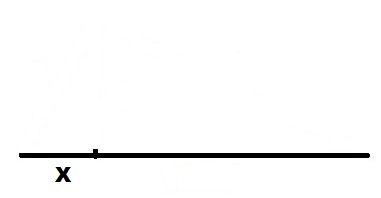
X
1
.
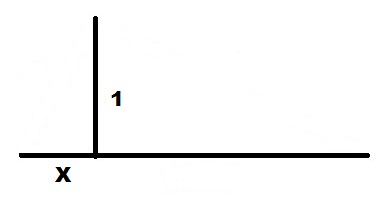
.
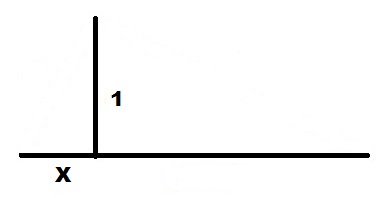
X
1
. .
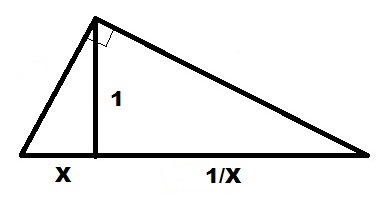
, , .
X
1
, . , . , 20, 16 (4 ), 4 (4 ).