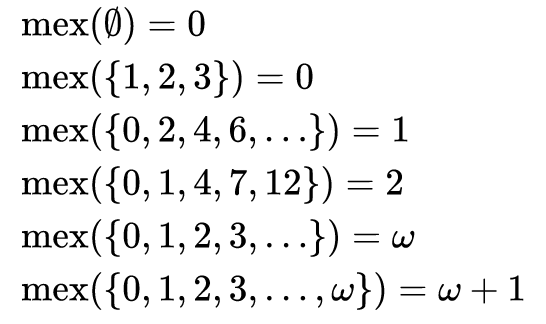
3つのアルゴリズムを分解し、それらのパフォーマンスを見ていきます。
カットの下でようこそ
序文
始める前に、私はあなたに言いたいです-なぜ私はこのアルゴリズムをまったく始めたのですか?
それはすべてOZONのパズルから始まりました。

問題からわかるように、数学では、数値のセットに対するMEX関数の結果は、このセットに属さないセット全体の最小値です。つまり、これは一連の加算の最小値です。「MEX」という名前は、「MinimumEXcluded」値の省略形です。
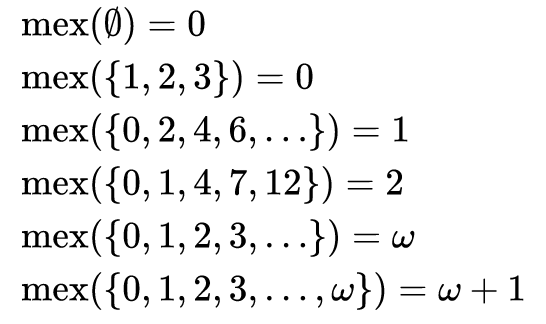
そして、ネットワークで噂された結果、MEXを見つけるための一般的に受け入れられているアルゴリズムがないことが判明しました...簡単な
解決策があり、追加の配列、グラフを備えたオプションがありますが、どういうわけかこれはすべてインターネットのさまざまな場所に散らばっていますこの問題に関する通常の記事は1つもありません。それで、この記事を書くというアイデアが生まれました。この記事では、MEXを見つけるための3つのアルゴリズムを分析し、速度とメモリの観点から何が得られるかを確認します。
コードはC#になりますが、通常、特定の構成はありません。
チェックの基本的なコードは次のようになります。
static void Main(string[] args)
{
//MEX = 2
int[] values = new[] { 0, 12, 4, 7, 1 };
//MEX = 5
//int[] values = new[] { 0, 1, 2, 3, 4 };
//MEX = 24
//int[] values = new[] { 11, 10, 9, 8, 15, 14, 13, 12, 3, 2, 0, 7, 6, 5, 27, 26, 25, 4, 31, 30, 28, 19, 18, 17, 16, 23, 22, 21, 20, 43, 1, 40, 47, 46, 45, 44, 35, 33, 32, 39, 38, 37, 36, 58, 57, 56, 63, 62, 60, 51, 49, 48, 55, 53, 52, 75, 73, 72, 79, 77, 67, 66, 65, 71, 70, 68, 90, 89, 88, 95, 94, 93, 92, 83, 82, 81, 80, 87, 86, 84, 107, 106, 104 };
//MEX = 1000
//int[] values = new int[1000];
//for (int i = 0; i < values.Length; i++) values[i] = i;
//
int total = 0;
int mex = GetMEX(values, ref total);
Console.WriteLine($"mex: {mex}, total: {total}");
Console.ReadKey();
}
そして、記事のもう1つのポイントとして、「配列」という言葉についてよく言及しますが、「セット」の方が正しいと思いますが、この仮定によって断ち切られる人たちに事前に謝罪したいと思います。
コメントに基づく注1:多くの人がO(n)に誤りを見つけました。彼らは、すべてのアルゴリズムがO(n)であり、「O」がどこでも異なっていても、実際には反復回数を比較しないと言っています。次に、安心のために、OをTに変更します。Tが多かれ少なかれ理解できる操作である場合:チェックまたは割り当て。ですから、私が理解しているように、誰にとっても簡単です。
コメントに基づく注2:元のセットが注文されていない場合を検討しています。これらのセットの並べ替えにも時間がかかります。
1)額の決定
「最小欠落数」をどのように見つけますか?最も簡単なオプションは、カウンターを作成し、カウンターに等しい数が見つかるまで配列を反復処理することです。
static int GetMEX(int[] values, ref int total)
{
for (int mex = 0; mex < values.Length; mex++)
{
bool notFound = true;
for (int i = 0; i < values.Length; i++)
{
total++;
if (values[i] == mex)
{
notFound = false;
break;
}
}
if (notFound)
{
return mex;
}
}
return values.Length;
}
}
最も基本的なケース。アルゴリズムの複雑さはT(n *セル(n / 2))..。{0、1、2、3、4}の場合、以降、すべての数値を反復処理する必要があります。15回の操作を行います。そして、5050の操作を含む100の完全な行の場合...まあまあのパフォーマンス。
2)スクリーニング
2番目に複雑な実装オプションはT(n)に適合します...まあ、またはほぼT(n)、数学者は狡猾であり、データの準備を考慮していません...少なくとも、最大数を知る必要がありますセットで。
数学的にはこんな感じです。
長さmのビット配列S(mは配列Vの長さ)が0で埋められます。1回のパスで、配列(S)の元のセット(V)が1に設定されます。その後、1回のパスで最初の空の値を見つけます。 mより大きいすべての値は単純に無視できます。配列にmまでの「不十分な」値が含まれている場合、それは明らかにmの長さよりも短くなります。
static int GetMEX(int[] values, ref int total)
{
bool[] sieve = new bool[values.Length];
for (int i = 0; i < values.Length; i++)
{
total++;
var intdex = values[i];
if (intdex < values.Length)
{
sieve[intdex] = true;
}
}
for (int i = 0; i < sieve.Length; i++)
{
total++;
if (!sieve[i])
{
return i;
}
}
return values.Length;
}
なぜなら 「数学者」は狡猾な人々です。次に、元の配列を通過するパスは1つだけであると言います。アルゴリズムT(n)...彼らは
座って、そのようなクールなアルゴリズムが発明されたことを喜んでいますが、真実はそうです。
最初に、元の配列
を調べて、配列S T1(n)でこの値をマークする必要があります。 次に、配列Sを調べて、そこで最初に使用可能なセルT2(n)を見つける必要があり
ます。一般に、すべての操作は複雑ではなく、すべての計算はT(n * 2)に簡略化できますが
、これは単純なソリューションよりも明らかに優れています...テストデータを確認しましょう。
- ケース{ 0、12、4、7、1 }の場合:額:11回の反復、ふるい分け:8回の反復
- { 0, 1, 2, 3, 4 }: : 15 , : 10
- { 11,…}: : 441 , : 108
- { 0,…,999}: : 500500 , : 2000
事実、「欠測値」が小さい場合、この場合、正面からの決定がより速くなることがわかります。アレイをトリプルトラバースする必要はありません。しかし、一般的に、大きな寸法では明らかにふるい分けに負けます。これはそれほど驚くべきことではありません。
「数学者」の観点からは-アルゴリズムは準備ができており、素晴らしいですが、「プログラマー」の観点からは-無駄なRAMの量と、見つけるための最後のパスのためにひどいです最初の空の値は明らかに加速されたいと思っています。
これを実行して、コードを最適化しましょう。
static int GetMEX(int[] values, ref int total)
{
var max = values.Length;
var size = sizeof(ulong) * 8;
ulong[] sieve = new ulong[(max / size) + 1];
ulong one = 1;
for (int i = 0; i < values.Length; i++)
{
total++;
var intdex = values[i];
if (intdex < values.Length)
{
sieve[values[i] / size] |= (one << (values[i] % size));
}
}
var maxInblock = ulong.MaxValue;
for (int i = 0; i < sieve.Length; i++)
{
total++;
if (sieve[i] != maxInblock)
{
total--;
for (int j = 0; j < size; j++)
{
total++;
if ((sieve[i] & (one << j)) == 0)
{
return i * size + j;
}
}
}
}
return values.Length;
}
ここで何をしましたか。まず、必要なRAMの量が64分の1に削減されました。
var size = sizeof(ulong) * 8;
ulong[] sieve = new ulong[(max / size) + 1];
その結果、sieveアルゴリズムは次の結果をもたらします。
- ケース{0、12、4、7、1}の場合:スクリーニング:8回の反復、最適化スクリーニング:8回の反復
- ケース{0、1、2、3、4}の場合:スクリーニング:10回の反復、最適化スクリーニング:11回の反復
- ケース{11、...}の場合:ふるい分け:108回の反復、最適化によるふるい分け:108回の反復
- ケース{0、...、999}の場合:スクリーニング:2000回の反復、最適化によるスクリーニング:1056回の反復
それで、速度理論の結論は何ですか?
T(n * 3)を全体としてT(n * 2)+ T(n / 64)に変換し、速度をわずかに上げ、RAMの容量を64分の1に減らしました。なんてこった)
3)並べ替え
ご想像のとおり、セット内の欠落している要素を見つける最も簡単な方法は、ソートされたセットを用意することです。
最速のソートアルゴリズムは「クイックソート」であり、T1(n log(n))の複雑さを持っています。そして、合計すると、T1(n log(n))+ T2(n)でMEXを見つけるための理論的な複雑さが得られます。
static int GetMEX(int[] values, ref int total)
{
total = values.Length * (int)Math.Log(values.Length);
values = values.OrderBy(x => x).ToArray();
for (int i = 0; i < values.Length - 1; i++)
{
total++;
if (values[i] + 1 != values[i + 1])
{
return values[i] + 1;
}
}
return values.Length;
}
ゴージャス。余分なものはありません。
反復回数を確認してください
- ケース{ 0、12、4、7、1 }の場合:最適化によるふるい分け:8、並べ替え:〜7回の反復
- ケース{0、1、2、3、4}の場合:最適化によるふるい分け:11回の反復、並べ替え:〜9回の反復
- { 11,…}: : 108 , : ~356
- { 0,…,999}: : 1056 , : ~6999
これらは平均値であり、完全に公平ではありません。ただし、一般的には、並べ替えに追加のメモリは必要なく、反復の最後のステップを単純化できることは明らかです。
注:values.OrderBy(X => x)の.ToArray() -はい、私はそのメモリがここで割り当てられているが、あなたは賢明にそれを行うならば、あなたは、配列を変更することができます知っている、いない、それをコピーし...
だから私が持っていました検索MEXのクイックソートを最適化するアイデア。このバージョンのアルゴリズムは、数学の観点からも、プログラミングの観点からも、インターネット上で見つかりませんでした。次に、途中で0からコードを記述し、どのように表示されるかを考えます。D
しかし、最初に、クイックソートが一般的にどのように機能するかを思い出しましょう。リンクを付けますが、実際にはクイックソートの通常の説明はありません。マニュアルの作成者自身がアルゴリズムについて話しているときに理解しているようです...
つまり、クイックソートとは次のとおりです。
順序付けられていない配列があります。 {0、12、4、7、1}
「乱数」が必要ですが、任意の配列を使用することをお勧めします。これは参照番号(T)と呼ばれます。
そして、2つのポインタ:L1-配列の最初の要素を調べ、L2は配列の最後の要素を調べます。
0、12、4、7、1
L1 = 0、L2 = 1、T = 1(Tは最後のもの愚かた)
第1の反復段階:
L1ポインターのみを使用する
までは、参照よりも大きい数が見つかるまで、配列に沿って右にシフトします。
この場合、L1は8に等しくなります。
反復の 第2段階:
L2ポインターをシフトします。
参照以下の数が見つかるまで、配列に沿って左にシフトします。
この場合、L2は1に等しくなります。配列の極値要素に等しい参照番号を取得し、そこでL2も調べました。
反復の第3段階:
L1およびL2ポインターの番号を変更し、ポインターを移動しないでください。
そして、反復の最初の段階に進みます。
L1ポインターとL2ポインターが等しくなるまで、これらの手順を繰り返します。値ではなく、ポインターです。それら。それらは1つのアイテムを指している必要があります。
ポインタがいくつかの要素に収束した後も、配列の両方の部分は並べ替えられませんが、確かに、「マージされたポインタ(L1とL2)」の片側には、T未満の要素があります。つまり、この事実により、配列を2つの独立したグループに分割し、さらに繰り返して異なるストリームに並べ替えることができます。
何が書かれているのかわからない場合は、ウィキの記事
クイックソートを書いてみましょう
static void Quicksort(int[] values, int l1, int l2, int t, ref int total)
{
var index = QuicksortSub(values, l1, l2, t, ref total);
if (l1 < index)
{
Quicksort(values, l1, index - 1, values[index - 1], ref total);
}
if (index < l2)
{
Quicksort(values, index, l2, values[l2], ref total);
}
}
static int QuicksortSub(int[] values, int l1, int l2, int t, ref int total)
{
for (; l1 < l2; l1++)
{
total++;
if (t < values[l1])
{
total--;
for (; l1 <= l2; l2--)
{
total++;
if (l1 == l2)
{
return l2;
}
if (values[l2] <= t)
{
values[l1] = values[l1] ^ values[l2];
values[l2] = values[l1] ^ values[l2];
values[l1] = values[l1] ^ values[l2];
break;
}
}
}
}
return l2;
}
実際の反復回数を確認しましょう。
- { 0, 12, 4, 7, 1 }: : 8, : 11
- { 0, 1, 2, 3, 4 }: : 11 , : 14
- { 11,…}: : 108 , : 1520
- { 0,…,999}: : 1056 , : 500499
次のことを考えてみましょう。配列{0、4、1、2、3}には欠落している要素がなく、その長さは5です。つまり、欠落している要素のない配列は、配列の長さ-1に等しいことがわかります。つまり、 m = {0、4、1、2、3}、長さ(m)==最大(m)+1。そして、この瞬間で最も重要なことは、配列内の値が次の場合にこの条件が真であるということです。再配置。そして重要なことは、この条件をアレイの一部に拡張できることです。つまり、次のようになります。
{0、4、1、2、3、12、10、11、14}配列の左側では、すべての数値が特定の参照番号(たとえば、5)よりも小さいことを知っています。右側では、左側の最小数を探すのに、大きいものはすべて意味がありません。
それら。パーツの1つに特定の値より大きい要素がないことが確実にわかっている場合は、この欠落している数値自体を配列の2番目のパーツで検索する必要があります。一般に、これは二分探索アルゴリズムがどのように機能するかです。
その結果、二分探索と組み合わせることで、MEX検索のクイックソートを簡素化するというアイデアを思いつきました。配列全体を完全に並べ替える必要はなく、検索する部分だけを並べ替える必要があることをすぐにお知らせします。
その結果、コードを取得します
static int GetMEX(int[] values, ref int total)
{
return QuicksortMEX(values, 0, values.Length - 1, values[values.Length - 1], ref total);
}
static int QuicksortMEX(int[] values, int l1, int l2, int t, ref int total)
{
if (l1 == l2)
{
return l1;
}
int max = -1;
var index = QuicksortMEXSub(values, l1, l2, t, ref max, ref total);
if (index < max + 1)
{
return QuicksortMEX(values, l1, index - 1, values[index - 1], ref total);
}
if (index == values.Length - 1)
{
return index + 1;
}
return QuicksortMEX(values, index, l2, values[l2], ref total);
}
static int QuicksortMEXSub(int[] values, int l1, int l2, int t, ref int max, ref int total)
{
for (; l1 < l2; l1++)
{
total++;
if (values[l1] < t && max < values[l1])
{
max = values[l1];
}
if (t < values[l1])
{
total--;
for (; l1 <= l2; l2--)
{
total++;
if (values[l2] == t && max < values[l2])
{
max = values[l2];
}
if (l1 == l2)
{
return l2;
}
if (values[l2] <= t)
{
values[l1] = values[l1] ^ values[l2];
values[l2] = values[l1] ^ values[l2];
values[l1] = values[l1] ^ values[l2];
break;
}
}
}
}
return l2;
}
反復回数を確認してください
- ケース{ 0、12、4、7、1 }の場合:最適化によるふるい分け:8、MEXソート:8回の反復
- { 0, 1, 2, 3, 4 }: : 11 , MEX: 4
- { 11,…}: : 108 , MEX: 1353
- { 0,…,999}: : 1056 , MEX: 999
さまざまなMEX検索オプションがあります。どちらが良いかはあなた次第です。
一般的に。私はスクリーニングが最も好きです 、そしてここに理由があります:
彼は非常に予測可能な実行時間を持っています。さらに、このアルゴリズムはマルチスレッドモードで簡単に使用できます。それら。配列をパーツに分割し、各パーツを別々のスレッドで実行します。
for (int i = minIndexThread; i < maxIndexThread; i++)
sieve[values[i] / size] |= (one << (values[i] % size));
必要なのは、ふるい[値[i] /サイズ]を書き込むときのロックだけです 。そしてもう1つ、アルゴリズムはデータベースからデータをアンロードするのに理想的です。たとえば、各ストリームに1000個のパックでロードできますが、それでも機能します。
ただし、メモリが大幅に不足している場合は、MEXの並べ替えが明らかに良くなります。
PS
ふるい分けアルゴリズムの「暫定版」を作って参加しようとしたOZONのコンテストから話を始めましたが、賞品を受け取ったことはなく、OZONはそれが不十分だと感じました...理由は何ですか?彼は決して告白しませんでした。 ..そして私も見たことがない勝者のコード。MEX探索問題をよりよく解決する方法について誰かが何かアイデアを持っていますか?