Clever Geek Handbook

トーナメントの並べ替え

私たちは、さまざまなヒープと、これらのヒープを使用したソートアルゴリズムに慣れ続けています。今日は、いわゆるトーナメントツリーがあります。
EDISONソフトウェア-ウェブ開発
EDISON .




, . , .



computer science ;-)
トーナメントソートの主なアイデアは、（メインアレイと比較して）比較的小さい補助ヒープを使用することです。これは、優先キューとして機能します。このヒープでは、下位レベルの要素が比較されます。その結果、小さい要素（この場合は、MIN-HEAPのツリー）が上がり、このヒープに含まれる配列要素の部分からの現在の最小値がルートに浮かびます。最小値は「勝者」の追加配列に転送され、その結果、ヒープが残りの要素を比較/移動します。これで、新しい最小値がツリーのルートにあります。このようなシステムでは、次の最小値の方が前の最小値よりも大きいことに注意してください。新しい「最小値」の配列が簡単に組み立てられ、新しい最小値が追加の配列の最後に追加されるだけです。



最小値を追加の配列に移動すると、メイン配列の次の要素の空き領域がヒープに表示され、その結果、すべての要素がキューの順序で処理されます。



主な微妙な点は、「勝者」に加えて「敗者」もいるということです。いくつかの要素が「勝者」の配列にすでに転送されている場合、未処理の要素がこれらの「勝者」よりも小さい場合、この段階でトーナメントツリーでそれらをふるい分けしても意味がありません。これらの要素を「勝者」の配列に挿入すると、コストがかかりすぎます（すでに終わらせることはできませんが、最初に終わらせるには、すでに挿入されているローをシフトする必要があります）。 「勝者」の配列に収まらなかった要素は、「敗者」の配列に送られます。残りの敗者に対してすべてのアクションが繰り返されると、次の反復の1つでトーナメントツリーを通過します。



このアルゴリズムの実装をインターネットで見つけるのは簡単ではありませんが、Rubyの明確で優れた実装がYouTubeで見つかりました。Javaコードは「リンク」セクションにも記載されていますが、ここではそれほど読みやすくはありません。 



  #         
  require_relative "pqueue"
	
  #     
  MAX_SIZE = 16

  def tournament_sort(array)
    #   ,   ""
    return optimal_tourney_sort(array) if array.size <= MAX_SIZE
    bracketize(array) #   ,   ""
  end
	
  #     
  def bracketize(array)
	
    size = array.size
    pq = PriorityQueue.new
    #    
    pq.add(array.shift) until pq.size == MAX_SIZE
    winners = [] #  ""
    losers = [] #  ""
		
    #      
    until array.empty?
			
      #  ""  ?
      if winners.empty?
        #      ""
        winners << pq.peek
        #     
        pq.remove 
      end
			
      #      ,   ""
      if array.first > winners.last
        pq.add(array.shift) #       
      else #        ""
        losers << array.shift #     ""
      end
			
      #     ,     ""
      winners << pk.peek unless pk.peek.nil?
      pq.remove #     
			
    end
		
    #   ,      - ?
    until pq.heap.empty?
      winners << pq.peek #     ""
      pq.remove #     
    end

    #   ""  , , ,
    #  "" -   
    return winners if losers.empty?
		
    #    ,    ""
    #   ""
    array = losers + winners
    array.pop while array.size > size
    bracketize(array) #   
		
  end
	
  #       
  def optimal_tourney_sort(array)
    sorted_array = [] #    
    pq = PriorityQueue.new
    array.each { |num| pq.add(num) } #     -
    until pq.heap.empty? #  -  
      sorted_array << pq.heap[0] 
      pq.remove #     
    end
    sorted_array #  
  end
	
  # 
  if $PROGRAM_NAME == __FILE__
    #  
    shuffled_array = Array.new(30) { rand(-100 ... 100) }
    #   
    puts "Random Array: #{shuffled_array}"
    #   
    puts "Sorted Array: #{tournament_sort(shuffled_array)}"
  end


これは単純な実装であり、「敗者」と「勝者」への各分割の後、これらの配列が結合され、結合された配列に対してすべてのアクションが再び繰り返されます。「負けた」要素が結合された配列の最初にある場合、トーナメントパイルをふるいにかけることで、「勝者」と一緒にそれらを並べ替えます。





この実装は非常に単純で明白ですが、効果的とは言えません。ソートされた「勝者」はトーナメントツリーを2回以上通過しますが、これは明らかに不要なようです。ここでの時間の複雑さは、対数2次、O（n log 2 n）であると想定しています。



マルチパスマージオプション



ふるいを通過する順序付けられた要素がトーナメントレースを繰り返し通過しない場合、アルゴリズムは著しく加速されます。



順序付けられていない配列がソートされた「勝者」とソートされていない「敗者」に分割された後、プロセス全体が「敗者」に対してのみ繰り返されます。新しいイテレーションごとに、「勝者」を持つ一連の配列が蓄積され、これはあるステップで「敗者」がなくなるまで続きます。その後は、「勝者」のすべての配列をマージするだけです。これらの配列はすべてソートされているため、このマージは最小限の労力で進行します。





この形式では、アルゴリズムはすでに有用なアプリケーションを見つけている可能性があります。たとえば、ビッグデータを扱う必要がある場合、プロセスの過程でトーナメントヒープを使用すると、順序付けられたデータのパケットが出てきます。これにより、他のすべてが処理されている間にすでに何かを行うことができます。配列のn個の要素の



それぞれがトーナメントツリーを1回だけ通過するため、O（log n）時間かかります。この実装では、アルゴリズムは最悪/平均時間の複雑さO（n log n）を持っています。



シーズンフィナーレ



ヒープのソートに関するシリーズはほぼ完了しています。それらのうち最も効果的なものについてはまだ述べていません。



参考文献



Tournament sort



Priority queue



Tournament sort in Java



The Theory Behind the The Theory Behind the z/Architecture Sort Assist Instructions



Using Tournament Trees to Sort



Tournament Sort Demo Ruby



Tournament Sort Visualization



Tournament Sort Data Structure UGC NET DS



Tournament Sort Algorithm — a Heapsort variant



:






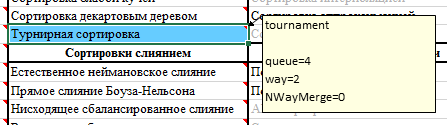
今日の並べ替えがAlgoLabアプリケーションに追加され、AlgoLabがそれを使用します-マクロでExcelファイルを更新します。



並べ替えの名前を含むセルへのコメントでは、いくつかの設定を指定できます。

変数wayはマルチウェイトーナメントツリーです（念のため、このツリーをバイナリーだけでなく、ターナリー、クォータナリー、ペンタリーにすることもできます）。キュー

変数は、元のキューのサイズ（ツリーの最下位レベルにあるノードの数）です。ツリーがいっぱいであるため、たとえば、way = 2でqueue = 5を指定すると、キューのサイズは最も近い2の累乗（この場合は最大8）に増加します。 可変NWayMerge

値は1または0です。マルチパスマージを使用するかどうかを示します。


More articles:


All Articles