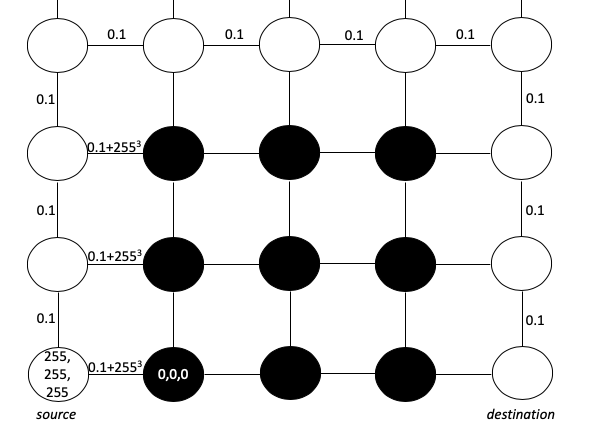
ダイクストラのアルゴリズムを思い出してください
ダイクストラのアルゴリズムは、最も一般的なグラフ理論アルゴリズムの1つです。有向グラフ上のノード間の最短経路を見つけるために使用されます。元のノードと、ノード間の既知のエッジ長から始めます。
最初に、ソースからすべてのノードまでの距離を割り当てます。ノードsはソースであるため、値0を取得します。残りは∞値を取得します。
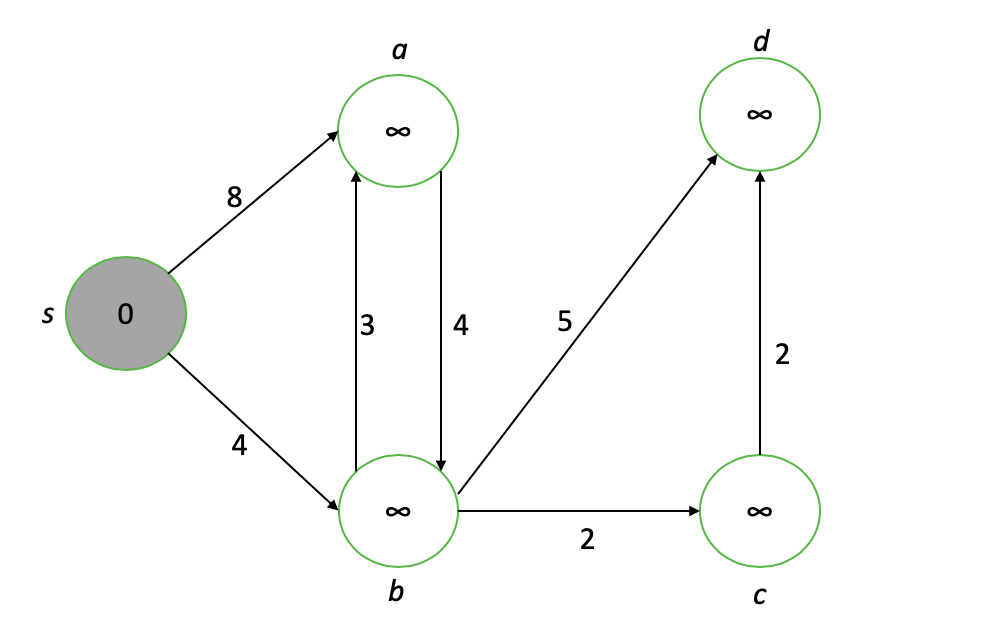
対象となるノードは、最小値(灰色で表示)、つまりsのrawノードです。最初に、対象のノードに隣接する各頂点を「弱め」、それらの値を現在の値の最小値または対象のノードの値と接続エッジの長さの合計に更新します...
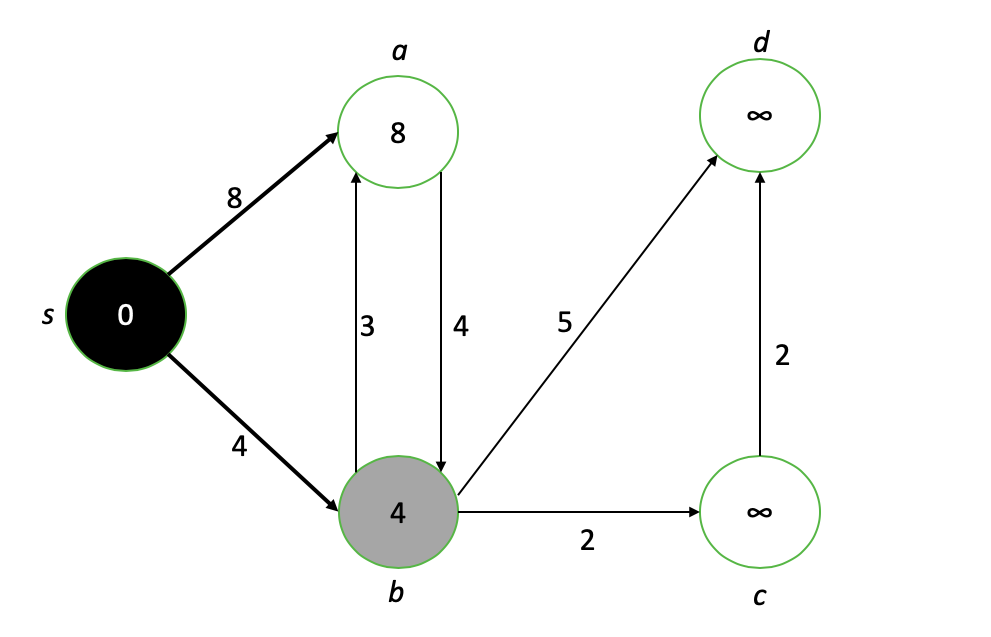
これでノードsは完成し(黒)、その隣接ノードaとbは新しい値を持っています。対象の新しいノードはbであるため、bの隣接ノードを「弱め」、bの最短パスの値を確定するプロセスを繰り返します。

各ノードを通過した後、ソースから各ノードまでの最短パス長を示すグラフが表示されます。
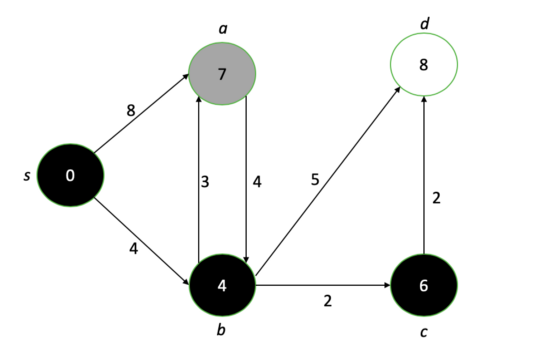


ダイクストラのアルゴリズムを実行した後の最終的な図。各ノードの数字は、元のノードからの可能な最短距離を表しています。
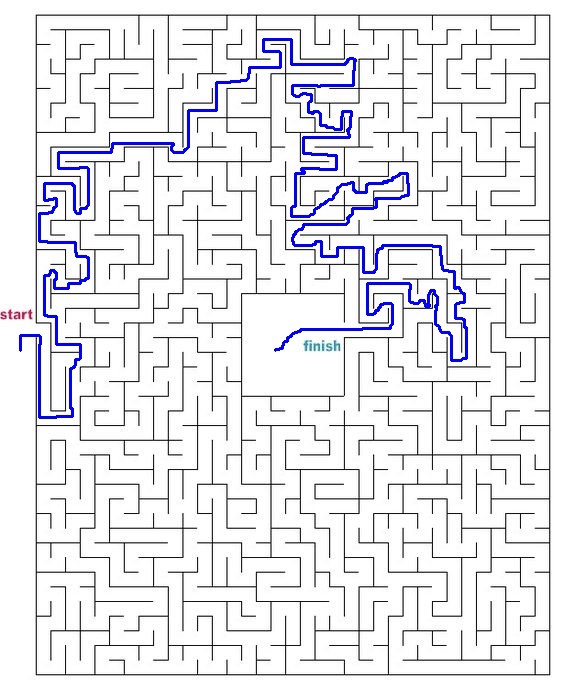
迷路画像の概念化

画像はピクセルのマトリックスと考えることができます。各ピクセル(簡単にするため)のRGB値は0,0,0(黒)または255,255,255(白)です。私たちの目標は、白から始まり、黒の境界線に到達しない最短経路を作成することです。この目標を表すために、各ピクセルをノードとして扱い、RGB値の違いに基づいて、エッジの長さを持つ隣接するピクセル間にエッジを描画できます。ユークリッド平方距離の式を使用し、0.1を追加してパスの長さがないことを確認します0-(ダイクストラのアルゴリズムの要件):
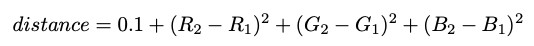
この式により、迷路の境界を横切る交差距離が過度に大きくなります。ご覧のように、出発地から目的地までの最短経路は、明らかにバリアを通過し、通過しません。
実装
Pythonで人気のコンピュータービジョンライブラリであるOpenCVを使用して、ピクセル値を抽出し、迷路画像を表示できます。迷路にポイントを追加して、開始位置と終了位置の座標も定義しましょう
import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread('maze.png') # read an image from a file using
cv2.circle(img,(5,220), 3, (255,0,0), -1) # add a circle at (5, 220)
cv2.circle(img, (25,5), 3, (0,0,255), -1) # add a circle at (5,5)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image
plt.show()
座標の追跡に役立つVertexクラスを作成します。また、距離の値を見つけたらパス全体を再構築できるように、親ノードを追跡したいとします。
class Vertex:
def __init__(self,x_coord,y_coord):
self.x=x_coord
self.y=y_coord
self.d=float('inf') #current distance from source node
self.parent_x=None
self.parent_y=None
self.processed=False
self.index_in_queue=None画像内のピクセルの2次元配置を表す頂点行列を作成する必要があります。これがダイクストラのアルゴリズムの基礎となります。また、生ノードを追跡するための優先順位の最小ヒープを持つキューを維持します。
def find_shortest_path(img,src,dst):
pq=[] #min-heap priority queue
imagerows,imagecols=img.shape[0],img.shape[1]
matrix = np.full((imagerows, imagecols), None)
#access matrix elements by matrix[row][col]
#fill matrix with vertices
for r in range(imagerows):
for c in range(imagecols):
matrix[r][c]=Vertex(c,r)
matrix[r][c].index_in_queue=len(pq)
pq.append(matrix[r][c])
#set source distance value to 0
matrix[source_y][source_x].d=0
#maintain min-heap invariant (minimum d Vertex at list index 0)
pq = bubble_up(pq, matrix[source_y][source_x].index_in_queue)エッジと頂点間のエッジの長さを見つけるのに役立ついくつかのヘルパー関数が必要です。
#Implement euclidean squared distance formula
def get_distance(img,u,v):
return 0.1 + (float(img[v][0])-float(img[u][0]))**2+(float(img[v][1])-float(img[u][1]))**2+(float(img[v][2])-float(img[u][2]))**2
#Return neighbor directly above, below, right, and left
def get_neighbors(mat,r,c):
shape=mat.shape
neighbors=[]
#ensure neighbors are within image boundaries
if r > 0 and not mat[r-1][c].processed:
neighbors.append(mat[r-1][c])
if r < shape[0] - 1 and not mat[r+1][c].processed:
neighbors.append(mat[r+1][c])
if c > 0 and not mat[r][c-1].processed:
neighbors.append(mat[r][c-1])
if c < shape[1] - 1 and not mat[r][c+1].processed:
neighbors.append(mat[r][c+1])
return neighborsこれで、ダイクストラのアルゴリズムを実装して、迷路画像のピクセルのすべての頂点に距離(d)値を割り当てることができます。
while len(pq) > 0:
u=pq[0] #smallest-value unprocessed node
#remove node of interest from the queue
pq[0]=pq[-1]
pq[0].index_in_queue=0
pq.pop()
pq=bubble_down(pq,0) #min-heap function, see source code
u.processed=True
neighbors = get_neighbors(matrix,u.y,u.x)
for v in neighbors:
dist=get_distance(img,(u.y,u.x),(v.y,v.x))
if u.d + dist < v.d:
v.d = u.d+dist
v.parent_x=u.x #keep track of the shortest path
v.parent_y=u.y
idx=v.index_in_queue
pq=bubble_down(pq,idx)
pq=bubble_up(pq,idx)これで、最短経路関数を呼び出して、迷路に解を描画できます。
img = cv2.imread('maze.png') # read an image from a file using opencv (cv2) library
p = find_shortest_path(img, (25,5), (5,220))
drawPath(img,p)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image on the screen
plt.show()

インターネット上の他の迷路を試してみましょう。



完全なソースコードは、GitHubのこちらから入手できます。
続き:Python学習プロジェクト:40行のコードインターフェイス(パート2)

SkillFactoryの有料オンラインコースを受講して、スキルと給与の注目の職業をゼロから習得する方法の詳細を学びます。
- 機械学習コース(12週間)
- データサイエンスの専門職をゼロからトレーニングする(12か月)
- 初心者レベルの分析職(9か月)
- «Python -» (9 )