これは、ヒープの並べ替えに関するシリーズの最後の記事です。これまでの講義では、速度の点で優れた結果を示すさまざまなヒープ構造について説明しました。これは疑問を投げかけます：ソートに関してはどのヒープが最も効率的ですか？答えは、今日見ていくものです。
前に見たファンシーヒープは問題ありませんが、最も効率的なヒープは、クリアが改善された標準ヒープです。
EDISON .
— « » — -, CRM-, , iOS Android.
;-)
ふるい分けされているもの、なぜそれがヒープ上で必要なのか、それがどのように機能するのか- 一連の記事の最初の部分で説明されています。
クラシックヒープソートの標準的なふるい分けは、おおよそ「正面」で機能します。サブツリーのルートからの要素はクリップボードに送信され、ブランチからの要素は比較結果に基づいて上方に移動します。すべては非常に単純ですが、比較が多すぎることがわかります。
親が子孫と比較されることはほとんどなく、基本的には子孫のみが比較されるため、上昇レーンでは比較が保存されます。通常のヒープソートでは、親は子孫と比較され、子孫は相互に比較されます。したがって、比較は同じ数の交換でほぼ半分になります。
それがどのように機能するか、具体的な例を見てみましょう。ヒープがすでにほぼ形成されている配列があるとします。残っているのはルートをふるいにかけることだけです。他のすべてのノードでは、条件が満たされます-子は親より大きくありません。
まず、クリアが実行されるノードから、大きな子孫に沿って下に行く必要があります。バイナリの束-つまり、左の子孫と右の子孫があります。子孫の大きい枝に行きます。この段階で、比較の主な数が発生します-左/右の子供が互いに比較されます。
最後のレベルで葉に到達したので、ブランチを決定しました。シフトする必要がある値です。しかし、ブランチ全体を移動する必要はありませんが、開始したルートよりも大きい部分だけを移動する必要があります。
したがって、ルートよりも大きい最も近いノードに分岐します。
最後のステップ-バッファー変数を使用して、ノードの値をブランチの上にシフトします。
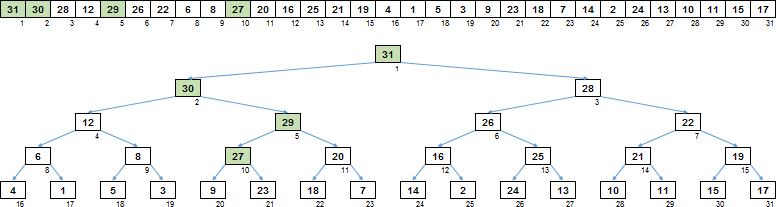
それでおしまい。昇順の消去により、配列から並べ替えツリーが形成されました。この場合、親は子孫よりも大きくなります。
最終的なアニメーション：
Python 3.7の実装
基本的なソートアルゴリズムは、通常のヒープソートと同じです。
#
def HeapSortBottomUp(data):
#
# -
# ( )
for start in range((len(data) - 2) // 2, -1, -1):
HeapSortBottomUp_Sift(data, start, len(data) - 1)
#
# .
for end in range(len(data) - 1, 0, -1):
#
#
data[end], data[0] = data[0], data[end]
#
#
#
HeapSortBottomUp_Sift(data, 0, end - 1)
return dataボトムシートへの降下は、別の機能で便利に/視覚的に取り出すことができます：
#
#
def HeapSortBottomUp_LeafSearch(data, start, end):
current = start
# ,
# ( )
while True:
child = current * 2 + 1 #
# ,
if child + 1 > end:
break
# ,
if data[child + 1] > data[child]:
current = child + 1
else:
current = child
# ,
child = current * 2 + 1 #
if child <= end:
current = child
return currentそして最も重要なこと-クリアリング、最初に下降し、次に上昇する：
#
def HeapSortBottomUp_Sift(data, start, end):
#
current = HeapSortBottomUp_LeafSearch(data, start, end)
# ,
#
while data[start] > data[current]:
current = (current - 1) // 2
# ,
#
temp = data[current]
data[current] = data[start]
#
# -
while current > start:
current = (current - 1) // 2
temp, data[current] = data[current], temp
Cコードはインターネットでも見つかりました
/*----------------------------------------------------------------------*/
/* BOTTOM-UP HEAPSORT */
/* Written by J. Teuhola <teuhola@cs.utu.fi>; the original idea is */
/* probably due to R.W. Floyd. Thereafter it has been used by many */
/* authors, among others S. Carlsson and I. Wegener. Building the heap */
/* bottom-up is also due to R. W. Floyd: Treesort 3 (Algorithm 245), */
/* Communications of the ACM 7, p. 701, 1964. */
/*----------------------------------------------------------------------*/
#define element float
/*-----------------------------------------------------------------------*/
/* The sift-up procedure sinks a hole from v[i] to leaf and then sifts */
/* the original v[i] element from the leaf level up. This is the main */
/* idea of bottom-up heapsort. */
/*-----------------------------------------------------------------------*/
static void siftup(v, i, n) element v[]; int i, n; {
int j, start;
element x;
start = i;
x = v[i];
j = i << 1;
/* Leaf Search */
while(j <= n) {
if(j < n) if v[j] < v[j + 1]) j++;
v[i] = v[j];
i = j;
j = i << 1;
}
/* Siftup */
j = i >> 1;
while(j >= start) {
if(v[j] < x) {
v[i] = v[j];
i = j;
j = i >> 1;
} else break;
}
v[i] = x;
} /* End of siftup */
/*----------------------------------------------------------------------*/
/* The heapsort procedure; the original array is r[0..n-1], but here */
/* it is shifted to vector v[1..n], for convenience. */
/*----------------------------------------------------------------------*/
void bottom_up_heapsort(r, n) element r[]; int n; {
int k;
element x;
element *v;
v = r - 1; /* The address shift */
/* Build the heap bottom-up, using siftup. */
for (k = n >> 1; k > 1; k--) siftup(v, k, n);
/* The main loop of sorting follows. The root is swapped with the last */
/* leaf after each sift-up. */
for(k = n; k > 1; k--) {
siftup(v, 1, k);
x = v[k];
v[k] = v[1];
v[1] = x;
}
} /* End of bottom_up_heapsort */純粋に経験的に-私の測定によると、昇順のヒープソートは通常のヒープソートより1.5倍高速です。
いくつかの情報（Wikipediaのアルゴリズムのページ、「リンク」セクションで引用されているPDFにある）によると、BottomUp HeapSortは、1万6千要素以上のかなり大きな配列の場合でも、平均してクイックソートよりも進んでいます。
参考文献
ボトムアップヒープソート
比較の数がほぼ最適なヒープソートのバリアント
ヒープを高速に構築する
ヒープソートの新しいバリアントは、平均してクイックソートです（nが非常に小さくない場合）。
シリーズ記事：
今日の並べ替えがAlgoLabアプリケーションに追加され、AlgoLabがそれを使用します-マクロでExcelファイルを更新します。