
圧倒的多数のケースにおけるビジネスの最適化は、線形計画法の使用に関連しています。この方法はかなり簡単です。さらに、ソリューションの存在と一意性に関する定理があります。
ただし、実際には、すべてが完全に単純というわけではありません。
最初の問題は、現実世界の条件の非線形性です。線形計画法を適用するには、線形化する必要があります。新しい変数を導入したり、重み係数を設定したりすることによって、線形方程式と不等式を介して非線形性をもっともらしい方法で設定する方法があります。この場合の生産上の問題を解決する場合、多数の変数、したがって方程式(不等式)を操作する必要があります。
極値問題を解く理論には、線形計画問題の解の安定性に関する定理があります。それによると、問題の領域が凸である場合にのみ、解は安定です。変数と不等式が多数ある場合、問題の領域が凸であるかどうかを確定することはできません。さらに、非凸性の確率が高くなります。
問題が安定していない場合、頂点をトラバースする開始点に応じて、異なる結果が得られます。
第二の問題-下からの変数の制限(x> h> 0)。線形計画法の実装では、常にゼロ以外のx値が提供されます。xがhと完全に等しい場合、これは変数xの値が本質的にゼロであることを意味します。実際には、このような「架空の」ボリューム(メソッドの尖度)は、「意味のある」変数に分散しています。このプラクティスの結果、最適なソリューションの概念が損なわれます。これは、そのようなソリューションが意思決定チェーンの多くのソリューションの1つである場合に特に重要です。
3番目の問題は管理上の問題です。線形計画法の結果は1つだけです。そして、最適に近い結果をどのように見るか?たとえば、結果のソリューションでは、ベンダーの評価が低くなっています。信頼できるサプライヤーのために、近い解決策があるかどうかを理解する方法。
輸送タスク
この例は、トランスポート線形計画問題に対応しています。
5つの運送業者があり(タスクは石炭の輸送用に設定されています)、2つの関税計算があります。関税の境界と関税自体は変更できます(これらはパラメトリックに設定されます)。

輸送は、ポイントツーポイント(石炭輸送の承認された方法による)および量として指定されます。
インターフェースの全体図。

輸送割当エリア。
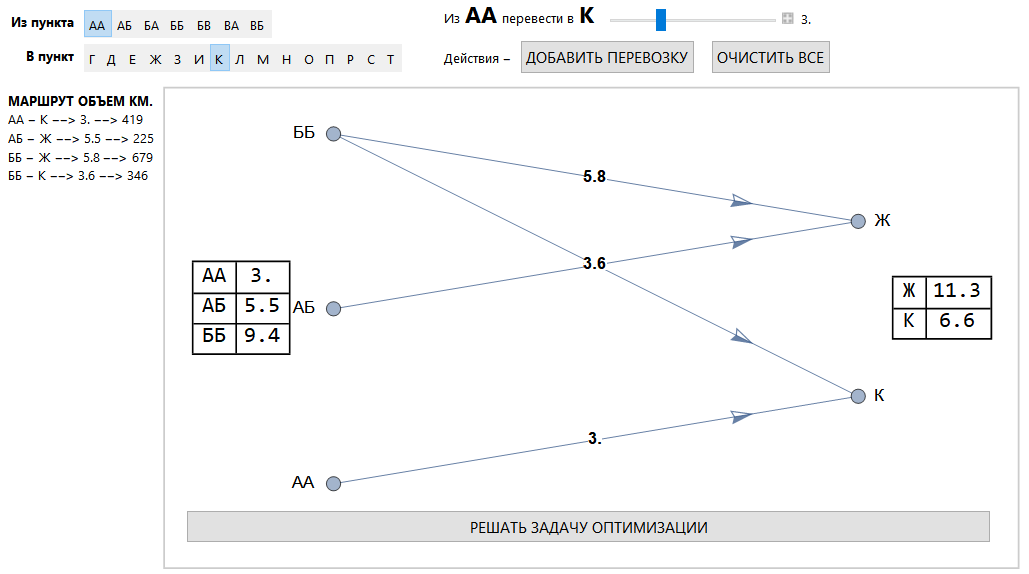
クラスター解法
1つの線形計画問題の代わりに、問題のクラスターが解決されます。問題の数は、関税のすべての可能な組み合わせに対応します。上記の出荷では、127個あります(左上の長方形の2番目の値)。

残りの正しい問題のセットから最適なソリューションが選択されます。各タスクは、関税の特定の組み合わせに最適なソリューションを提供します。上記のソリューションは、特定の範囲の最大値を構成します。
クラスター方式が優れている理由:
- ソリューションの安定性についての理解があります。
- そのような条件が存在しない別の組み合わせがあるため(そのような変数が存在しないため)、下からバインドされた変数の「架空の」ボリュームはありません。
- 主観的な条件(評価、好み)は、標準の線形計画法を使用して導入できます。
出荷数が多い場合は、次の図(フラグメント)があります。
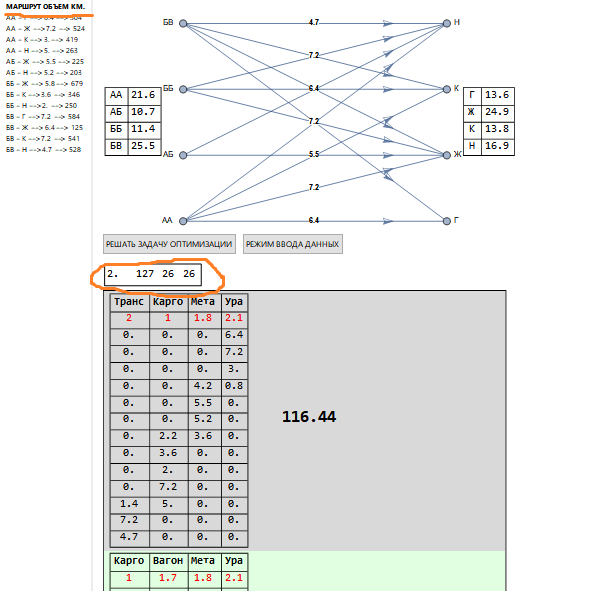
左上隅のソリューションの上にある四角形(オレンジ色で強調表示)には、以前よりも他の値が示されています。127-組み合わせ(以前と同様、関税率の構造に関連しています)、26-解決されている残りの正しい問題の数に対応しています。運送業者の名前の下に使用されている料金は赤で表示され、輸送の列はルートのリストに対応しています(オレンジ色の下線付き)。
使用する方法により、結果を理解し、同様のソリューションを評価し、代替案を選択する際に専門的な経験を使用して、特定のビジネスを実行する複雑さを考慮できることに注意することが重要です。