ここで、qは粒子の電荷、r ijは粒子間の距離、Cは測定単位の選択に応じて定数になります。SIでは-、SGS-1では、私のプログラムでは(エネルギーは電子ボルト、距離はオングストロームで、電荷は素電荷で表されます)Cはおよそ14.3996に等しくなります。
それで、あなたは何を言うのですか?対応する用語をペアのポテンシャルに追加するだけで完了です。ただし、MDモデリングでは、ほとんどの場合、周期的な境界条件が使用されます。シミュレートされたシステムは、その仮想コピーの無限の数によって四方から囲まれています。この場合、システムの各仮想画像は、クーロンの法則に従ってシステム内のすべての荷電粒子と相互作用します。そして、クーロン相互作用は距離(1 / rのような)で非常に弱く減少するため、そのような距離からは計算しないと言って、それを却下することはそれほど簡単ではありません。フォーム1 / xのシリーズは発散します。その量は、原則として無期限に増加する可能性があります。そして今、スープを塩漬けしませんか?それはあなたを電気で殺しますか?
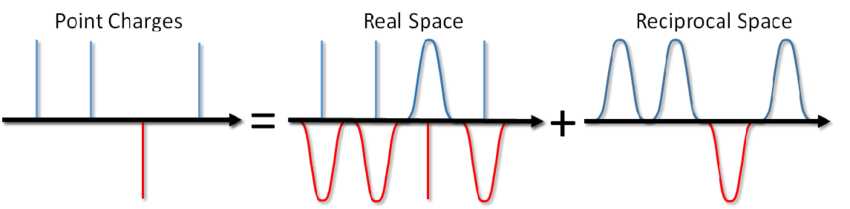
...スープを塩漬けするだけでなく、周期的な境界条件下でのクーロン相互作用のエネルギーも計算できます。この方法は、1921年にイオン結晶のエネルギーを計算するためにEwaldによって提案されました(ウィキペディアでも確認できます)。この方法の本質は、ポイントチャージをスクリーニングし、スクリーニング関数を差し引くことです。この場合、静電相互作用の一部は短時間作用型になり、標準的な方法で簡単に遮断できます。残りの長距離部分は、フーリエ空間で効果的に合計されます。Blinovの記事または同じ本のFrenkelとSmithが見ることができる結論を省略して、Ewald sumと呼ばれる解決策をすぐに書き留めます。
ここで、αはフォワードスペースとリバーススペースでの計算の比率を調整するパラメーター、kは加算が行われる逆空間のベクトル、Vはシステムのボリューム(フォワードスペース)です。最初の部分(E real)は短距離であり、他のペアのポテンシャルと同じサイクルで計算されます。前の記事のreal_ewald関数を参照してください。最後の寄与(Eonst)は自己相互作用の補正であり、粒子の座標に依存しないため、「定数部分」と呼ばれることがよくあります。その計算は取るに足らないので、エヴァルド和の2番目の部分(E rec)、相互空間での総和。当然のことながら、エワルドの導出時には分子動力学は存在せず、MDでこの方法を最初に使用したのは誰なのかわかりませんでした。現在、MDに関する本には、そのプレゼンテーションが一種のゴールドスタンダードとして含まれています。予約するために、アレンはFortranでコード例を提供しました。幸いにも、シーケンシャルバージョン用にCで記述されたコードがまだあります。それを並列化するだけです(変数の宣言やその他の重要ではない詳細は省略できました)。
void ewald_rec()
{
int mmin = 0;
int nmin = 1;
// iexp(x[i] * kx[l]),
double** elc;
double** els;
//... iexp(y[i] * ky[m])
double** emc;
double** ems;
//... iexp(z[i] * kz[n]),
double** enc;
double** ens;
// iexp(x*kx)*iexp(y*ky)
double* lmc;
double* lms;
// q[i] * iexp(x*kx)*iexp(y*ky)*iexp(z*kz)
double* ckc;
double* cks;
//
eng = 0.0;
for (i = 0; i < Nat; i++) //
{
// emc/s[i][0] enc/s[i][0]
// elc/s , .
elc[i][0] = 1.0;
els[i][0] = 0.0;
// iexp(kr)
sincos(twopi * xs[i] * ra, els[i][1], elc[i][1]);
sincos(twopi * ys[i] * rb, ems[i][1], emc[i][1]);
sincos(twopi * zs[i] * rc, ens[i][1], enc[i][1]);
}
// emc/s[i][l] = iexp(y[i]*ky[l]) ,
for (l = 2; l < ky; l++)
for (i = 0; i < Nat; i++)
{
emc[i][l] = emc[i][l - 1] * emc[i][1] - ems[i][l - 1] * ems[i][1];
ems[i][l] = ems[i][l - 1] * emc[i][1] + emc[i][l - 1] * ems[i][1];
}
// enc/s[i][l] = iexp(z[i]*kz[l]) ,
for (l = 2; l < kz; l++)
for (i = 0; i < Nat; i++)
{
enc[i][l] = enc[i][l - 1] * enc[i][1] - ens[i][l - 1] * ens[i][1];
ens[i][l] = ens[i][l - 1] * enc[i][1] + enc[i][l - 1] * ens[i][1];
}
// K-:
for (l = 0; l < kx; l++)
{
rkx = l * twopi * ra;
// exp(ikx[l]) ikx[0]
if (l == 1)
for (i = 0; i < Nat; i++)
{
elc[i][0] = elc[i][1];
els[i][0] = els[i][1];
}
else if (l > 1)
for (i = 0; i < Nat; i++)
{
// iexp(kx[0]) = iexp(kx[0]) * iexp(kx[1])
x = elc[i][0];
elc[i][0] = x * elc[i][1] - els[i][0] * els[i][1];
els[i][0] = els[i][0] * elc[i][1] + x * els[i][1];
}
for (m = mmin; m < ky; m++)
{
rky = m * twopi * rb;
// iexp(kx*x[i]) * iexp(ky*y[i])
if (m >= 0)
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][m] - els[i][0] * ems[i][m];
lms[i] = els[i][0] * emc[i][m] + ems[i][m] * elc[i][0];
}
else // m :
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][-m] + els[i][0] * ems[i][-m];
lms[i] = els[i][0] * emc[i][-m] - ems[i][-m] * elc[i][0];
}
for (n = nmin; n < kz; n++)
{
rkz = n * twopi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < rkcut2) //
{
// (q[i]*iexp(kr[k]*r[i])) -
sumC = 0; sumS = 0;
if (n >= 0)
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][n] - lms[i] * ens[i][n]);
cks[i] = ch * (lms[i] * enc[i][n] + lmc[i] * ens[i][n]);
sumC += ckc[i];
sumS += cks[i];
}
else // :
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][-n] + lms[i] * ens[i][-n]);
cks[i] = ch * (lms[i] * enc[i][-n] - lmc[i] * ens[i][-n]);
sumC += ckc[i];
sumS += cks[i];
}
//
akk = exp(rk2 * elec->mr4a2) / rk2;
eng += akk * (sumC * sumC + sumS * sumS);
for (i = 0; i < Nat; i++)
{
x = akk * (cks[i] * sumC - ckc[i] * sumS) * C * twopi * 2 * rvol;
fxs[i] += rkx * x;
fys[i] += rky * x;
fzs[i] += rkz * x;
}
}
} // end n-loop (over kz-vectors)
nmin = 1 - kz;
} // end m-loop (over ky-vectors)
mmin = 1 - ky;
} // end l-loop (over kx-vectors)
engElec2 = eng * * twopi * rvol;
}
コードに関するいくつかの説明:関数は、すべてのkベクトルとすべての粒子について、kベクトルと粒子の半径ベクトルのベクトル積から複素指数(コードへのコメントではブラケットから虚数単位を削除するためにiexpと示されています)を計算します。この指数は、粒子の電荷で乗算されます。次に、すべての粒子のそのような積の合計が計算され(E recの式の内部合計)、フレンケルでは電荷密度と呼ばれ、ブリノフでは構造因子と呼ばれます。そして、これらの構造的要因に基づいて、粒子に作用するエネルギーと力が計算されます。 k-ベクトルの成分(2π* l / a、2π* m / b、2π* n / c)は、3つの整数l、mおよびnによって特徴付けられます、ユーザー指定の制限までのサイクルで実行されます。パラメータa、b、cはそれぞれ、シミュレーションされたシステムの次元x、y、zでの次元です(直方体形状のシステムでは結論は正しいです)。このコードでは、1 / a、1 / b、および1 / cは、変数ra、rb、およびrcに対応しています。各値の配列は、実数部と虚数部の2つのコピーで表示されます。 1つの次元内の次の各k-ベクトルは、前の1つを複素数で乗算することにより、前の1つから反復的に取得されます。emc / sおよびenc / s配列は、すべてのmに入力されます及びnは、それぞれ、配列ELC / sの場所それぞれに対する値Lのゼロインデックスで> 1のLメモリを節約するためです。
並列化の目的で、サイクルの順序を「逆」にして、外側のサイクルが粒子を超えるようにすることが有利です。そして、ここに問題があります-この関数は、すべての粒子(電荷密度)の合計を計算する前にのみ並列化できます。以降の計算はこの量に基づいて行われ、すべてのスレッドが作業を終了したときにのみ計算されるため、この関数を2つに分割する必要があります。 1つ目は電荷密度を計算し、2つ目はエネルギーと力を計算します。 2番目の関数でも数量q iが必要になることに注意してください。前のステップで計算された、各粒子および各k-ベクトルのiexp(kr)。そして、ここでは2つのアプローチがあります。それをもう一度再計算するか、覚えてください。
最初のオプションはより多くの時間がかかり、2番目のオプションはより多くのメモリ(パーティクルの数* k-ベクトルの数* sizeof(float2))です。私は2番目のオプションで解決しました:
__global__ void recip_ewald(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the first part : summ (qiexp(kr)) evaluation
{
int i; // for atom loop
int ik; // index of k-vector
int l, m, n;
int mmin = 0;
int nmin = 1;
float tmp, ch;
float rkx, rky, rkz, rk2; // component of rk-vectors
int nkx = md->nk.x;
int nky = md->nk.y;
int nkz = md->nk.z;
// arrays for keeping iexp(k*r) Re and Im part
float2 el[2];
float2 em[NKVEC_MX];
float2 en[NKVEC_MX];
float2 sums[NTOTKVEC]; // summ (q iexp (k*r)) for each k
extern __shared__ float2 sh_sums[]; // the same in shared memory
float2 lm; // temp var for keeping el*em
float2 ck; // temp var for keeping q * el * em * en (q iexp (kr))
// invert length of box cell
float ra = md->revLeng.x;
float rb = md->revLeng.y;
float rc = md->revLeng.z;
if (threadIdx.x == 0)
for (i = 0; i < md->nKvec; i++)
sh_sums[i] = make_float2(0.0f, 0.0f);
__syncthreads();
for (i = 0; i < md->nKvec; i++)
sums[i] = make_float2(0.0f, 0.0f);
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
ik = 0;
for (i = id0; i < N; i++)
{
// save charge
ch = md->specs[md->types[i]].charge;
el[0] = make_float2(1.0f, 0.0f); // .x - real part (or cos) .y - imagine part (or sin)
em[0] = make_float2(1.0f, 0.0f);
en[0] = make_float2(1.0f, 0.0f);
// iexp (ikr)
sincos(d_2pi * md->xyz[i].x * ra, &(el[1].y), &(el[1].x));
sincos(d_2pi * md->xyz[i].y * rb, &(em[1].y), &(em[1].x));
sincos(d_2pi * md->xyz[i].z * rc, &(en[1].y), &(en[1].x));
// fil exp(iky) array by complex multiplication
for (l = 2; l < nky; l++)
{
em[l].x = em[l - 1].x * em[1].x - em[l - 1].y * em[1].y;
em[l].y = em[l - 1].y * em[1].x + em[l - 1].x * em[1].y;
}
// fil exp(ikz) array by complex multiplication
for (l = 2; l < nkz; l++)
{
en[l].x = en[l - 1].x * en[1].x - en[l - 1].y * en[1].y;
en[l].y = en[l - 1].y * en[1].x + en[l - 1].x * en[1].y;
}
// MAIN LOOP OVER K-VECTORS:
for (l = 0; l < nkx; l++)
{
rkx = l * d_2pi * ra;
// move exp(ikx[l]) to ikx[0] for memory saving (ikx[i>1] are not used)
if (l == 1)
el[0] = el[1];
else if (l > 1)
{
// exp(ikx[0]) = exp(ikx[0]) * exp(ikx[1])
tmp = el[0].x;
el[0].x = tmp * el[1].x - el[0].y * el[1].y;
el[0].y = el[0].y * el[1].x + tmp * el[1].y;
}
//ky - loop:
for (m = mmin; m < nky; m++)
{
rky = m * d_2pi * rb;
//set temporary variable lm = e^ikx * e^iky
if (m >= 0)
{
lm.x = el[0].x * em[m].x - el[0].y * em[m].y;
lm.y = el[0].y * em[m].x + em[m].y * el[0].x;
}
else // for negative ky give complex adjustment to positive ky:
{
lm.x = el[0].x * em[-m].x + el[0].y * em[-m].y;
lm.y = el[0].y * em[-m].x - em[-m].x * el[0].x;
}
//kz - loop:
for (n = nmin; n < nkz; n++)
{
rkz = n * d_2pi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < md->rKcut2) // cutoff
{
// calculate summ[q iexp(kr)] (local part)
if (n >= 0)
{
ck.x = ch * (lm.x * en[n].x - lm.y * en[n].y);
ck.y = ch * (lm.y * en[n].x + lm.x * en[n].y);
}
else // for negative kz give complex adjustment to positive kz:
{
ck.x = ch * (lm.x * en[-n].x + lm.y * en[-n].y);
ck.y = ch * (lm.y * en[-n].x - lm.x * en[-n].y);
}
sums[ik].x += ck.x;
sums[ik].y += ck.y;
// save qiexp(kr) for each k for each atom:
md->qiexp[i][ik] = ck;
ik++;
}
} // end n-loop (over kz-vectors)
nmin = 1 - nkz;
} // end m-loop (over ky-vectors)
mmin = 1 - nky;
} // end l-loop (over kx-vectors)
} // end loop by atoms
// save sum into shared memory
for (i = 0; i < md->nKvec; i++)
{
atomicAdd(&(sh_sums[i].x), sums[i].x);
atomicAdd(&(sh_sums[i].y), sums[i].y);
}
__syncthreads();
//...and to global
int step = ceil((double)md->nKvec / (double)blockDim.x);
id0 = threadIdx.x * step;
N = min(id0 + step, md->nKvec);
for (i = id0; i < N; i++)
{
atomicAdd(&(md->qDens[i].x), sh_sums[i].x);
atomicAdd(&(md->qDens[i].y), sh_sums[i].y);
}
}
// end 'ewald_rec' function
__global__ void ewald_force(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the second part : enegy and forces
{
int i; // for atom loop
int ik; // index of k-vector
float tmp;
// accumulator for force components
float3 force;
// constant factors for energy and force
float eScale = md->ewEscale;
float fScale = md->ewFscale;
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
for (i = id0; i < N; i++)
{
force = make_float3(0.0f, 0.0f, 0.0f);
// summ by k-vectors
for (ik = 0; ik < md->nKvec; ik++)
{
tmp = fScale * md->exprk2[ik] * (md->qiexp[i][ik].y * md->qDens[ik].x - md->qiexp[i][ik].x * md->qDens[ik].y);
force.x += tmp * md->rk[ik].x;
force.y += tmp * md->rk[ik].y;
force.z += tmp * md->rk[ik].z;
}
md->frs[i].x += force.x;
md->frs[i].y += force.y;
md->frs[i].z += force.z;
} // end loop by atoms
// one block calculate energy
if (blockIdx.x == 0)
if (threadIdx.x == 0)
{
for (ik = 0; ik < md->nKvec; ik++)
md->engCoul2 += eScale * md->exprk2[ik] * (md->qDens[ik].x * md->qDens[ik].x + md->qDens[ik].y * md->qDens[ik].y);
}
}
// end 'ewald_force' function
英語でコメントを残すことを許してくれるといいのですが、コードは実質的にシリアルバージョンと同じです。コードがあってもアレイが一次元を失ったという事実によるものより読みやすくなった:ELC / S [i]は[L] 、EMC / S [i]は[M]及びENC / S [I] [n]を一次元になっEL、EM、およびen、配列lmc / sおよびckc / s-変数lmおよびckに(粒子ごとの次元はなくなりました。各粒子ごとにそれを格納する必要がなくなったため、中間結果は共有メモリに蓄積されます)。残念ながら、すぐに問題が発生しました。配列emおよびenグローバルメモリを使用せず、毎回メモリを動的に割り当てないように、静的に設定する必要がありました。それらの要素の数は、コンパイル段階でNKVEC_MXディレクティブ(1次元のk-ベクトルの最大数)によって決定され、最初のnky / z要素のみが実行時に使用されます。さらに、すべてのkベクトルのエンドツーエンドインデックスと同様のディレクティブが表示され、これらのベクトルの総数NTOTKVECが制限されました。ユーザーがディレクティブで指定されたよりも多くのkベクトルを必要とする場合、問題が発生します。エネルギーを計算するために、どのブロックがこの計算をどの順序で実行するかは重要ではないため、インデックスがゼロのブロックが提供されます。変数akkで計算された値がシリアルコードは、シミュレートされたシステムのサイズにのみ依存し、初期化段階で計算できます。私の実装では、シリアルコードは各k-ベクトルのmd-> exprk2 []配列に格納されます。同様に、k-ベクトルのコンポーネントはmd-> rk []配列から取得されます。ここではメソッドがそれに基づいているため、既製のFFT関数を使用する必要があるかもしれませんが、それを行う方法はまだわかりませんでした。
さて、今度は何かを数えましょうが、同じ塩化ナトリウムです。 2000ナトリウムイオンと同じ量の塩素を取ってみましょう。電荷を整数として設定し、例えばこの仕事からペアポテンシャルをとりましょう... 図2aのように、開始構成をランダムに設定して、少し混ぜます。システムの体積は、室温での塩化ナトリウムの密度(2.165 g / cm 3)に対応するように選択します。クーロンの法則に従って静電気を単純に考慮し、Ewald総和を使用して、これらすべてを短時間(5フェムト秒の10'000ステップ)から始めましょう。結果の構成をそれぞれ図2bと2cに示します。エヴァルトの場合、システムは彼がいない場合よりも少し合理化されているようです。総和を使用すると、総エネルギー変動が大幅に減少することも重要です。

図2. NaClシステムの初期構成(a)および10'000統合ステップ後:単純な方法(b)およびEwaldスキーム(c)。
結論の代わりに
図で得られた構造はNaCl結晶格子ではなく、ZnS格子に対応していることに注意してください。これは、すでにペアポテンシャルに関する不満です。静電気を考慮することは、分子動力学モデリングにとって非常に重要です。それが長い距離で作用するので、それは結晶格子の形成に責任がある静電相互作用であると考えられています。確かに、この位置から、アルゴンなどの物質が冷却中にどのように結晶化するかを説明することは困難です。
前述のエワルド法に加えて、静電気を説明する他の方法もあります。たとえば、このレビューを参照してください。