Clever Geek Handbook

VKデータの誕生日のパラドックス

こんにちは！



私はVKから入手できるデータを使用して誕生日のパラドックスをチェックすることにしました。



誕生日のパラドックスとは何ですか？



質問に答えてみてください：2人が同じ誕生日を0.5の確率で持つには、部屋に何人必要ですか？（日付と月）。誕生日のパラドックスはこの質問に答えます。



この問題を解決するには、いくつかの前提条件を強調することをお勧めします。



  1. モデルには、2月29日=>モデルの年間365日はありません。
  2. 365日のそれぞれの可能性は同じです。


もちろん、誕生日が等しい可能性があることは完全に現実的ではありません-子供の誕生日に影響する季節的な影響があります。私はあなたがどれに影響するかを推測できると思います...



ほとんどの人は問題の質問に直感的に答えます：180。論理的に見える、180人が0.5の同一の誕生日の確率（合計365日）。誕生日のパラドックスを聞いたことがない人は皆、この直感についてです。正解は、実際には180未満、さらには150未満、さらには100未満です。23。



一致する誕生日が少なくとも1つ必要です。一致する誕生日がない確率を見つけることができます。

P(" ")=365∗364∗363∗...∗(365−k+1)365k=365!365k∗(365−k)!

...

アイデアは次のとおりです。私は最初の人と彼の誕生日を覚えてから2人目を覚え、彼の誕生日が1人目の誕生日と一致しない確率を計算します。3回目よりさらに先に、彼の誕生日が1回目と2回目の誕生日と一致しない確率を計算します。



方程式を解くと、23人が必要であり、誕生日が一致する確率は0.5073であり、100人の場合、確率は0.9999です。



VKデータのパラドックスを見てみましょうか？



理論的には、23人の場合、誕生日が一致する確率は0.5073、50人の場合は0.97、100人の場合は0.99です。VK APIで確認してみましょう。



1. VKで大きなコミュニティを選択します。VkontakteでMDKグループを採用することにしました...



まず、必要な列を含むcsvファイルを作成します。 



with open('vk_data.csv', 'w') as new_file:
                # csv
                fieldnames = ['id', 'bdate', 'bmonth', 'byear', 'dandm']

                csv_writer = csv.DictWriter(new_file, fieldnames=fieldnames, delimiter=',')

                csv_writer.writeheader()

                newDict = dict()


API経由でVKにログインし、必要なパブリックを設定します 

vk_session = vk_api.VkApi('username', 'password')
                vk_session.auth()

                vk = vk_session.get_api()
                
                vk_group = vk.groups.getMembers(group_id = 'mudakoff', fields = 'bdate')


VKontakteの解析を開始します。そのAPIを使用すると、解析できるユーザーは1000人だけなので、ループを作成します。 



for i in range(0, 20):
                    vk_group = vk.groups.getMembers(group_id = 'mudakoff', offset = 1000 * i,  fields = 'bdate')
                    for k in range(0, 1000):
                        try:
                            new_file.write(str(vk_group['items'][k]["id"]) + ',' + str(vk_group['items'][k]["bdate"]).replace('.', ','))
                            new_file.write('\n')
                        except:
                            pass


理論的には、誕生日の確率は同じであると想定しましたが、実際にはどうなりますか？誕生日のヒストグラムを作成します。



画像



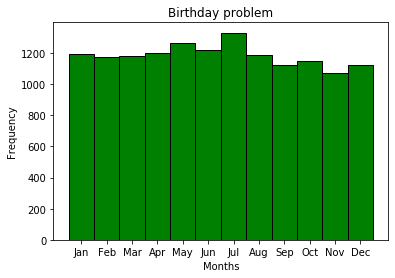
月別の誕生日は、確率が等しいイベントではありません。これは、一般的に非常に論理的です。これは、誕生日の問題を解決するための前提条件です。明らかに、場所によって季節ごとのイベントが異なります。何らかの理由で、7月はMDKサブスクライバーの誕生日として最も人気のある月です。



私は、50人の任意の人々のグループで同じ誕生日の少なくとも2人がいる確率を経験的に推定します。これを行うために、テーブルから50行のサブサンプルが発生するサイクルを書きました。条件内のこれらの50行について、誕生日の一致をチェックしました。一致した場合、それをカウンター変数に記憶しました。その後、サイクル長で除算して確率を取得します。 



fifty = df["dandm"].sample(n = 50)
for i in range(0, 1000):
    fifty = df["dandm"].sample(n = 50)
    for j in fifty.duplicated():
        if j == True:
            counter = counter + 1
            break
print(':', counter / 1000)


確率は理論データと一致する0.97の領域で得られます。



出力



理論が経験主義とどのように関連しているかを見るのは興味深いことでした。この場合、データは理論を裏付けています。サンプルが十分に大きいため、結果は代表的なものであることに注意してください-20,000人。



資源



  1. ハーバード大学。誕生日の問題、確率の性質| 統計110。URL：www.youtube.com/watch?v=LZ5Wergp_PA&t=150s。アクセス：2020年7月8日
  2. 誕生日の問題。URL：en.wikipedia.org/wiki/Birthday_problem。アクセス：2020年7月8日>


More articles:


All Articles