
次に、スウェーデンのクロナの割引曲線を作成してみます。
この投稿は、Finmath forFintechコースの一部としての私の3番目のビデオ講義「割引曲線の作成」の適応バージョンです。
したがって、クロナの割引曲線は、毎日の宿泊料金になります。私たちが最初に知っているのは、いわゆる基本料金、つまり短期預金(ローン)の料金です。さらに、1年から30年の範囲の既知のスワップがあります。この方法を説明するために、10年までの曲線をプロットします。現在の市場データ値はこの画像で見ることができます:

曲線のプロットを開始するには、いくつかの仮定を行う必要があります。
簡単にするために、私たちのスワップは、6か月ごとに定期的に支払いが行われる固定フローティングスワップであると仮定しましょう。以下は、1年間のスワップの図です。最初は基本レートがゼロパーセントであることを私たちは知っています。公正なスワップ価格を計算するには、6か月の割引係数と12か月の割引係数の値を知る必要があります。フローティング「レッグ」として何がありますか?各範囲の平均夜間値を支払うと仮定します。つまり、最大6か月のフローティング「レッグ」の値です。これは、180日間の夜間の平均値になります。 12か月のポイントのフローティングレッグは同じですが、ここでのみ、181日目から360日目までの合計があります。
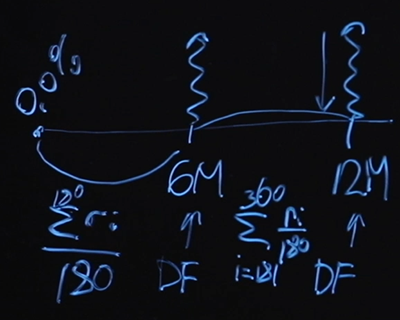
この平均化方法は広く知られています。これはオーバーナイトインデックススワップと呼ばれ、市場の製品で非常に頻繁に使用されます。フローティングレッグは、ここでは期間中の平均として定義されます。
基本料金とスワップのコストはわかっています。明らかに、公正な価格の公式を「真正面から」書くと、未知数が多すぎます。 6か月間の割引係数、12か月間の割引係数はわかりません。また、最初の1つを除いて、金利の値もわかりません。未知数が多すぎて、方程式が1つだけです。

次の仮説は、この問題の解決に役立ちます。ポイントゼロでの金利がわかっています。これが基本レートです。金利は直線的に変化すると仮定します。 12ヶ月の時点での金利の値をXとして指定しましょう。
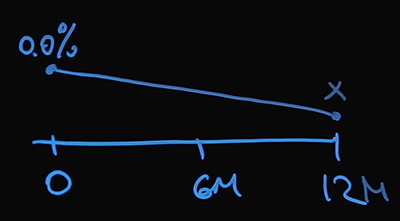
6ヶ月でX / 2(ゼロとXの間の算術平均)になり、任意の日の金利の値を見つけることができます。そして、ポイント6か月と12か月の変動金利を計算するのに難しいことは何もありません。
それでは、割引係数に移りましょう。宿泊料金に基づく割引曲線を使用します。したがって、6か月の時点での割引係数は、各時点での180の割引係数の積であり、これは明らかにXのある種の関数になります。12
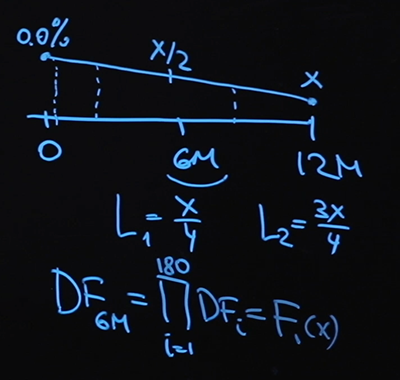
か月の時点での割引係数は同じ方法で作成されますが、必要な違いは1つだけです。より多くの乗数。これもXの関数になります。

したがって、割引係数はXで表され、変動率の1番目と2番目の値もあります。方程式の作成に移りましょう。スワップ価格の値がわかっている、たとえばそれがPに等しいとしましょう。公正価格の式を思い出してください。Pに12か月の時点での割引係数を掛けて、次の合計に

等しくする必要があります。1日の割引係数は、次の式で決定されることに注意してください。
ここで、R iは、利子率の値です。1年に360日あると仮定して、数値360を使用します(これはカレンダーの非常に一般的な規則です)。任意の時点で、我々は、割引率を表現する方法を知ってrを私は線形補間を用いて、Xの用語で表現しました。私たちの方程式は未知数が1つしかないことが判明し、数値法を使用して解くことができます。これを行う方法-Pythonコードを参照してください。
したがって、1年の時点でのレートの値を見つける方法を知っています。線形補間の仮定を使用し、市場からわかっているスワップ値に基づいて、Xの値を見つけます。ここで、曲線の最初のセクションをプロットしました。

ここで、2年間のスワップ価格を計算するには、6か月、12か月、18か月、および2年の時点での値が必要です。前回と全く同じ仮定を使用します。目的のレートの値をYと呼び、補間線に関する仮定を使用して、曲線の2番目のセクションを復元しましょう。したがって、段階的に、私たちは終わりに到達します-10年の時点まで。

このメソッドはブートストラップと呼ばれます。それは完全ではないか、唯一の正しいものではありませんが、実装して理解するのに十分簡単です-ブートストラップメソッドは開始レベルとして最適です。

割引曲線が見つかりました。それは私たちに何を与えますか?正式に言えば、これらは10年までの将来の任意の時点でのオーバーナイトレートの値です。あなたはおそらく「誰がそれを必要としているのか」と尋ねるでしょう。確かに、クライアントがあなたのところに来て、「567日で始まる1日預金を開きたい」と言うシナリオを想像するのは難しいです。これはかなり理解できない状況であり、構築された曲線をそのような直接的な形で知覚するべきではありません。
将来、たとえば7年半の間に何らかの支払いがあると想像してみましょう。質問:現在の値をどのようにして知ることができますか?
これはまさに割引曲線が答える質問です。曲線の各ポイントを調べ、各ポイントで割引係数を計算し、そのポイントで7年半の旅を終了し、結果の割引係数を見つけて、支払いを掛けます。これは適正価格になります。
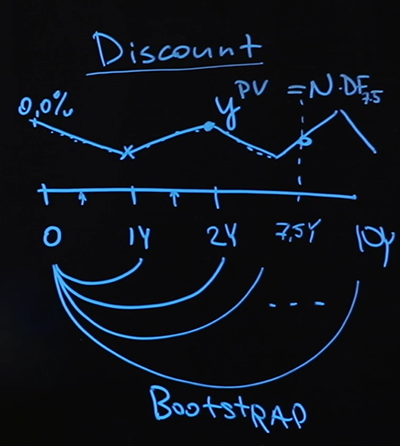
私が使用したモデル、つまり、どの浮動レートを使用したか、中間値をどのように補間したか、そして一般に、補間を選択したという事実は、私が持っているデータの種類によって大きく決まりました。データはほとんどありませんでした。基本レートとスワップ値は1つだけでした。より多くのデータが利用できる場合、またはデータが異なる場合は、モデルを変更する可能性があります。ただし、ブートストラップ方式(最初に短いセクションに曲線をプロットし、次に以前に取得した値に基づいてさらにプロットする場合)は引き続き適用されます。
ここで、割引曲線に加えて、LIBOR曲線(TIBOR、EURIBORなど)が必要であることを思い出してください。違いは、計算のためにモデルに追加するツールにあります。 LIBORを含む契約を探し、同様の方法で、ブートストラップ方式を使用して、LIBOR曲線を再構築します。
実際のLIBOR曲線を作成する必要がある場合は、それを作成するために使用するツールに十分注意し、使用するモデルを慎重に評価してください。この場合、夜間割引を使用しましたが、LIBOR曲線を作成するには別の方法が必要です。ほとんどの場合、割引は商品に応じて3か月または6か月ごとに行われます。十分なデータがある場合は、LIBOR曲線、EURIBOR曲線、TIBOR曲線などをプロットできます。
クライアントが「10年ではなく134ヶ月間、25日ごとに変動LIBORを支払う金利スワップが欲しい」という言葉を持って来た場合、これは問題ではありません。 LIBOR曲線があり、補間の仮定を使用して、任意の時点でLIBOR値を復元できます。各ポイントでの割引曲線の値がわかっているので、すべての支払いを計算して、これらの変動支払いのバランスをとる固定「レッグ」の価格を見つけることもできます。したがって、いくつかの曲線をプロットすることにより、絶対にすべての機器の公正な価格値を見つけることができます。
それでは、ハイライトをもう一度見てみましょう。私は入手可能なデータを取り、いくつかの仮定を立てました。まず、支払いスケジュール:各当事者が固定レッグとフローティングレッグを支払う頻度、頻度。次に、フローティングレッグへの賭けをどのように計算しますか? 3番目の仮定は、線形ベット補間についてです。これら3つの仮定すべてを使用して、いくつかの非線形方程式を定式化し、数値的に解きました。 Jupyterノートブックはここにあります。続いて、1年の最短セグメントから始めて、2年、3年など、最大10年の間隔で曲線を再構築しました。これは、あらゆる機器の評価に使用できる割引曲線です。この方法はブートストラップと呼ばれます。最初にカウントした曲線のセグメントを2番目のステップで使用します。それ以外の場合は、2番目のステップで得たものを3番目のステップに使用し、カーブが完全に形成されるまで続けます。
変動金利のトピックで「変動」しなくなり、スワップの金利の中にバニラが見つかることを願っています。また、ブートストラップ方式を使用して任意の曲線を作成することもできます。
このシリーズのすべての記事