数学の未来は？

英国の数学者KevinBuzzardによるプレゼンテーションのこの翻訳では、次のxkcdコミックが絶望的に時代遅れになっていることがわかります。

数学の未来は何ですか？

• 1990年代に、コンピューターは人間よりもチェスを上手にプレイし始めました。
• 2018年、コンピューターは人間よりもGoのプレイに優れています。
• 2019年、人工知能研究者のChristian Szegedyは、10年後には、コンピューターが人間よりも優れた定理を証明するようになると私に語った。

もちろん、彼は間違っているかもしれません。または多分彼は正しいです。



私はこれを信じています。10年後、コンピューターは私たちが初期の大学院生のレベルで悲惨な定理を証明するのに役立ちます。数学のどの分野ですか？誰がこの研究分野に関与するかによって異なります。



人工知能の典型的なパターンは次のとおりです。最初は非常に愚かで、その後突然賢くなります。自然な問題は、位相遷移がいつ発生し、人工知能が突然非常にスマートになるのかということです。回答：誰もこれを知りません。明らかなことは、より多くの人々がこの研究分野に関与しているほど、これはより早く起こるということです。

証拠とは何ですか？

優秀な学生、研究数学者、そしてコンピューターに証拠は何かと尋ねると、彼らの答えは何ですか？優秀な学生とコンピューターの答えは一致し、次のようになります。

証明は、選択されたシステムの公理、以前に証明された推論規則、および定理で構成される論理的な一連のステートメントであり、最終的にはステートメントが証明されることになります。

もちろん、研究数学者の答えはそれほど理想的ではありません。数学者にとって、証明の定義は、他の経験豊富な数学者が証明と見なすものです。または、Annals ofMathematicsまたはInventionesでの公開が認められているもの。



ただし、これには小さな問題があります。次のスクリーンショットは、世界で最も権威のある数学ジャーナルの1つであるAnnals ofMathematicsからのものです。











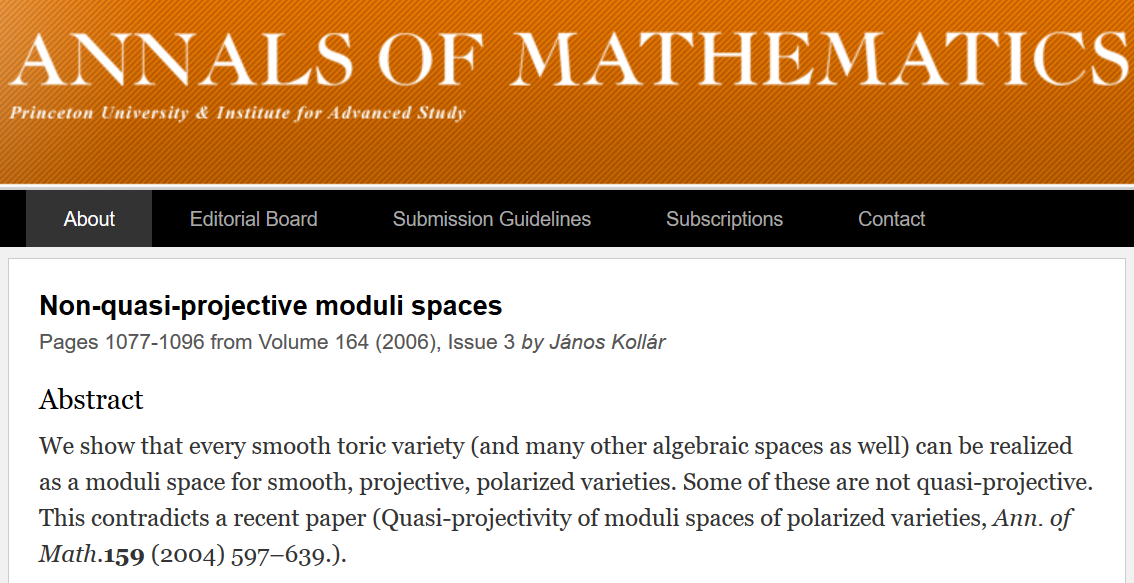
2番目の記事は文字通り最初の記事と矛盾します。著者はこれについて公然と注釈に書いています。私の知る限り、Annals of Mathematicsは、これらの作品に対する反論を発表したことはありません。経験豊富な数学者が正しいと考える作業はどれですか？あなたがこの分野で働いている場合にのみ、これについて知ることができます。



出力：現代の数学では、何かが証明であるかどうかについての意見は時間とともに変化します（たとえば、「ある」から「ない」に変わる可能性があります）。







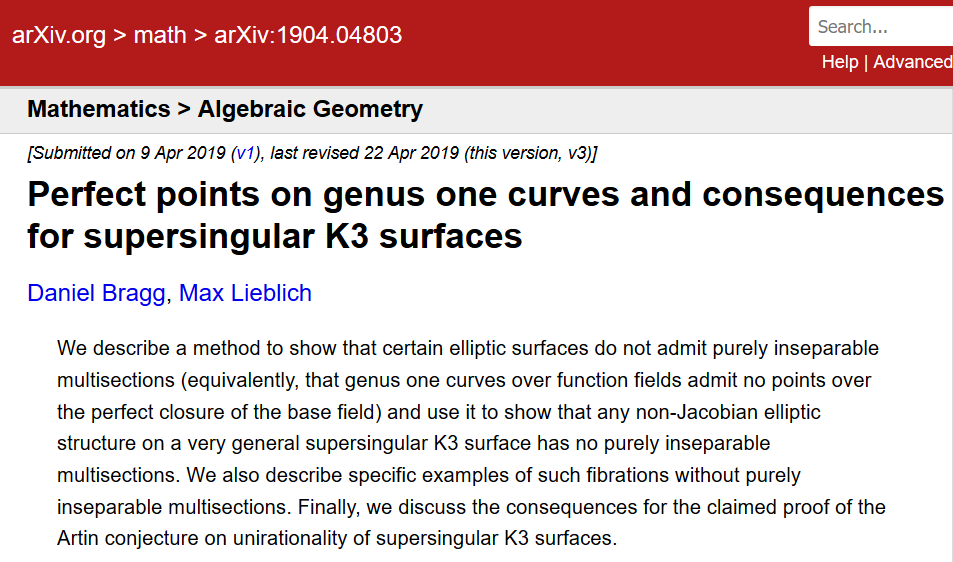
この短い2019年の記事は、Inventionesに掲載された別の重要な2015年の記事が誤った補題に大きく依存していることを指摘しています。 2016年に人々がこの重要な仕事を研究するためにワークショップを組織していたという事実にもかかわらず、これは2019年まで気づかれませんでした。



数学の基礎に貢献したフィールズ賞受賞者のウラジミール・ボエボドスキーは、次のように述べています。「人々に信頼されている著者が、検証するのは難しいが、他の正しい議論と同様の技術的に複雑な議論を書いた場合、この議論はほとんどありません。何でも詳細にチェックされます。」



発明は、2015年の論文に対する反論を発表したことはありません。



結論：公開されている重要な数学が間違っていることが判明することがあります。さらに、将来的には、公表された証拠に対する反論が増えることは間違いありません。



たぶん、p-adic Langlandsプログラムでの私の仕事は、間違った結果に基づいています。または、より楽観的に、正しい結果を得るためですが、完全な証拠はありません。



私たちの研究が再現不可能である場合、それを科学と呼ぶことができますか？ラングランズのp-adicプログラムが人類によって有用なことをするために使われることは決してないだろうと私は99.9％確信しています。私の数学の仕事が役に立たず、100％正しいことが保証されている場合、それは時間の無駄です。..。そこで私は研究をやめ、コンピューターで「有名な」数学をテストすることに集中することにしました。



2019年、Balakrishnan、Dogra、Mueller、Tuitman、Vonkは、2つの変数で特定の4次方程式のすべての合理的な解を見つけました。明示的に：

$$

この計算は、算術において重要な用途があります。証明は、高速で参照されていないアルゴリズムを使用したマグマ（クローズドソース）での計算に大きく依存しています。すべてのコンピューティングをsageのようなオープンソースシステムに移植することは困難です。ただし、これを行う予定はありません。



したがって、証拠のいくつかは隠されたままです。そしておそらくそれは永遠に隠されたままになります。これは科学ですか？

数学のギャップ

• 1993 . .
• 1994 , .
• 1995 , , . , , , . , , , .

レビューのために数学的な記事を受け取ったレビューアは何をすべきですか？レビューアの仕事は、「論文で使用されている方法が、論文の主な結果を証明するのに十分強力であることを確認すること」であると主張されています。



方法が強力であるが、著者がそうではない場合はどうなりますか？これは、私たちの証拠が不完全なときに状況が発生する方法です。これが、私たちの定理が実際に証明されているかどうかについての議論が生じる方法です。これは、私たちが生徒に数学について教える方法ではありません。



もちろん、専門家はどの文献が信頼できるのか、どれが信頼できないのかを知っています。しかし、私が信頼できる文献を見つけるには、専門家である必要がありますか？

数学の大きなギャップ

展示物A

単純な有限グループの分類。専門家は、単純な有限グループの完全な分類があると主張しています。私は専門家を信頼しています。

• 1983年に、分類の専門家による証明が発表されました。
• 1994年に、専門家は間違いを発見しました（しかし、ハエから象を吹き飛ばさないようにしましょう？）
• 2004年には、1000ページ以上の作品が公開されました。フィールドエキスパートのAschbacherは、エラーが修正されたと主張し、12巻の完全な証拠を公開する計画を発表しました。
• 2005年には、12巻のうち6巻のみが発行されました。
• 2010年には、12巻のうち6巻のみが発行されました。
• 2017年には、12巻のうち6巻のみが発行されました。
• 2018年には、第7巻と第8巻が発行され、発行は2023年までに完了する予定であることに注意してください。

プロジェクトを率いる3人のうち1人が亡くなりました。他の2つは70を超えています。

展示物B

アベリア表面の潜在的なモジュール性。 1年前、私の著名な大学院生のToby Geeと3人の共著者が、285ページのプレプリントを公開しました。その結果、完全に実在するフィールド上のAbelianサーフェスはモジュール化される可能性があります。



彼らの証拠は、3つの未発表のプレプリント（2018年に1つ、2015年に1つ、1990年代に1つ）、2007年のインターネットメモ、ドイツ語の未発表の論文、および後に主な主張が反駁された論文を引用しています。さらに、13ページに次のテキストが表示されます。

, Arthur’s multiplicity formula GSp4, [Art04]. , , [GT18], , [Art13] [MW16a, MW16b]. , twisted weighted fundamental lemma, [CL10], . , [A24], [A25], [A26] [A27] [Art13], .

これは科学だと正直に言えますか？



リンク[CL10]は次のようになります。



私の大学院生と共著者が必要とする作品は公開されたことがありません。ほとんどの場合、ステートメントは正しいです。おそらく証明可能です。



そして、これらは[Art13]からの参照リンクです。





昨年、私はこれらのリンクについてアーサーに尋ねました、そして彼はまだ仕事の準備ができていないと私に言いました。もちろん、ジム・アーサーは天才です。彼は数々の権威ある賞を受賞しています。しかし、彼も75歳です。

展示物C

Gaitsgory –Rozenblyum。最近、無限のカテゴリーが人気を博しています。それらは時間とともにさらに重要になります。フィールズの受賞者であるピーター・ショルツの作品は、無限のカテゴリーに基づいています。



JacobLurieが1000ページ以上の作品を書いています$$-分類され、私の仕事に多くの詳細が含まれています。 Gaitsgory – Rozenblyumは、$$-カテゴリ。ただし、時間を節約するために多くの引数を省略しました。 「省略された証拠は他の場所に表示されます。」



Gaitsgoryにどれだけ足りないのか聞いた。彼はそれが約100ページであると答えました。私はルリーにこれについてどう思うか聞いた。彼は、「数学者は、詳細を省略した場合の快適さは大きく異なります」と答えました。



数学の動きが速すぎませんか？私が「専門家」である場合、完全に実際のフィールド上のアベリアの表面は潜在的にモジュール化されていると信じるべきですか？正直、もう自分のことはわかりません。



私が先週行ったカーネギーメロン大学での会議で、Markus Rabeは、Googleがarxiv.orgからの数学のプレプリントを翻訳するプログラムに取り組んでいると私に話しました。コンピュータ検証に適した言語に。最近、私の学生の記事に依存している作品を見ましたが、[Art13]の100ページの欠落については何も言及していません。

最後の間違い

これは非常に興味深い例です。原作はJ.Functに掲載されました。アナル。 2013年に。作業に大きなエラーがあります（反対方向の不平等）。このエラーは、2017年にS. Gouezelが、コンピューター化されたプルーフチェックプログラム（Isabelle）を使用して議論を形式化したときに発見されました。



Gouezelと元の作品の作者によって新しい議論が提示されます。新しい作品はレビューする必要はありません。コンピューターは新しい引数を100％チェックしました。この方法は、定理を証明するのに十分強力であることが判明しました。そして、「証明」とは、古典的な「純粋な」証明の定義を意味します。これは、私たちが生徒に教えるものです。証明のすべての詳細は、読者が利用できます。科学は再現可能です。これが私たちが生徒たちに教える数学です。これは数学です。



これが私が数学だと思う他の例です：

• 学生または修士レベルの典型的な証明
• 何万人もの数学者によって十分に文書化され、研究されてきた重要な結果の典型的な100年前の証拠
• Gonthier、Asperti、Avigad、Bertot、Cohen、Garillot、Le Roux、Mahboubi、O'Connor、Ould Biha、Pasca、Rideau、Solovyev、Tassi、ThéryoftheFeith-Thompsonの定理の正式な証明。
• 次の数学者による正式な著者の証明：Hales、Adams、Bauer、Dat Tat Dang、Harrison、Truong Le Hoang、Kaliszyk、Magron、McLaughlin、Thang Tat Nguyen、Truong Quang Nguyen、Nipkow、Obua、Pleso、Rute、Solovyev、An Hoai Thi Ta 、Trung Nam Tran、Diep Thi Trieu、Urban、Ky Khac Vu、およびZumkellerによるKeplerの推測の証明。

---

ケビンが彼の主要部分であるマイクロソフトリサーチのレオデモウラによって開発されたリーンでの数学的証明の正式な検証に移ったので、これでプレゼンテーションのテキストは終わりです。残念ながら、例はスライドに含まれていませんでした。







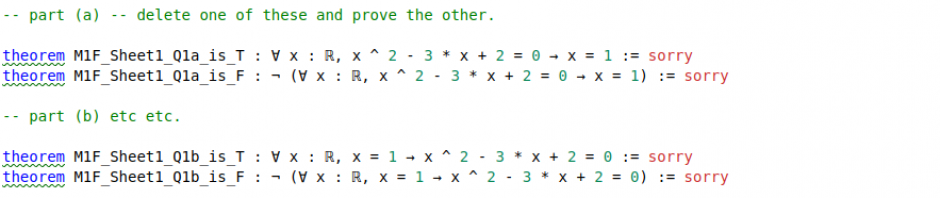
著者は数学的証明の正式な検証に大いに熱心であり、私が強くお勧めするこのトピックに関する非常に興味深いXenaブログを持っています。