こんにちは住民！粘土の足のある巨像は、コンピューターサイエンスのトレーニングなしでプログラマーと呼ぶことができるものです。基本を自信を持って習得することで、「車輪を作り直さない」ことができ、ソフトウェアアーキテクチャに効果的なソリューションを組み込むことができます。これにより、テストとリファクタリングのエラーと過剰なコストが排除されます。
他のプログラマーがおおよその制限について話し合っているときに、気分が悪くても問題ありません。経験豊富な専門家でさえ、コンピューターサイエンスを忘れているという事実のために間違いを犯します。
この本が必要な理由
私の（著者の）仲間の開発者の多くは、さまざまな分野からこの職業に就きました。コンピュータサイエンスの高等教育を受けている人もいます。写真や数学を学んだり、大学を卒業したことのない人もいます。
近年、プログラマーはいくつかの理由でコンピューターサイエンスを学びたいとますます熱心になっていることに気づきました。
- 優れたプログラマーになること。
- インタビュー中にアルゴリズムに関する質問に答えるため。
- コンピュータサイエンスの分野での好奇心を満たすため、または最終的に、かつてはこの主題を習得する機会がなかったことを後悔するのをやめるためです。
この本は皆さんのためのものです。
多くの人がここでそれ自体が興味深いトピックを見つけるでしょう。私は、この知識が実際の（非学術的な）状況でどのように役立つかを示しようとしました。この本を読んだ後は、コンピュータサイエンスの基礎コースを学んだ後と同じ知識を身につけ、その応用方法を学んでほしいと思います。
簡単に言えば、この本の目的は、コンピューターサイエンスをよりよく理解することで、より熟練した経験豊富なプログラマーになるのを支援することです。20年間の大学教育と専門的な経験を1冊にまとめることはできません...しかし、私は最善を尽くします。ここで、「はい、今は理解しています」と言えるトピックを少なくとも1つ見つけて、知識を仕事に応用してください。
エディションにないもの
この本の意味は、読者がコンピュータサイエンスをよりよく理解し、実際に知識を適用するのを助けることであり、4年間の研究に完全に取って代わるものではありません。
特に、これは証拠の本ではありません。実際、第2巻では書籍、証明の方法が考えられるが、標準的なアルゴリズムは、通常、証明なしでここに提示されています。読者がこれらのアルゴリズムの存在について学び、詳細に立ち入ることなくそれらを使用する方法を学ぶという考えです。学部生と大学院生向けに書かれた証明本として、Cormen、Leiserson、Rivest、Steinによるアルゴリズム入門を強くお勧めします（著者は通常、略語CLRS）。
これもプログラミングの本ではありません。int型の番号を使用する場合とdoubleを使用する場合のガイドライン、またはループとは何かについての説明はありません。読者は、アルゴリズムを説明するために使用される疑似コードのリストを理解できることが期待されます（この本のすべてのプログラムは、C言語に基づく疑似コードで書かれています）。この本の目的は、コンピュータサイエンスの概念を、読者にすでに馴染みのあるプログラミング手法と結び付けることです。
10.動的プログラミング
10.1。不足しているフィールドの問題
n×nのチェスボードにいくつかの正方形が欠けているとします。フィールドを逃さずに最大のk×kのボードを見つける方法は？
これまでにこのような問題に直面したことがない場合は、数分かけてソリューションを作成し、アルゴリズムの実行時間を決定してください。
この問題に直面して、私は次のように推論しました。各チェッカーボードフィールドは、最大の領域の多くに属することができますが、左上隅にできるのはそのうちの1つだけです。左上隅である最大の無傷の領域のサイズで各ボックスにマークを付けると、そのような最大のマークが付いたボックスが目的の領域に対応します。
ボードがn×nマトリックスとして表され、対応するフィールドが存在する場合は各セルに1が含まれ、存在しない場合は0が含まれるとします。現在のセル値が0の場合、対応するフィールドは存在せず、連続するセグメントの一部にすることはできないため、変更する必要はありません。値が1の場合、下と右にある3つのセルの最小値より1大きい数に置き換えることができます。
マトリックスの各セルを1回変更します。これには、セルの値がゼロかどうかの確認、最大3つのセルの値の確認、新しいセル値の書き込みが含まれます。これらの各操作にはO（1）時間がかかるため、チェッカーボード全体の処理にかかる時間は次のようになります。
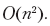
これは、アルゴリズムの2次ではなく線形の実行時間であることに注意してください-チェスボードn（nはフィールドの総数であると想定し、nは入力データの量であるという通常の規則に従います）フィールド（一部は存在しない）、したがって、アルゴリズムによって費やされる合計時間は、フィールドの数に比例します。チェス盤のサイズを√n×√nとより正確に表すと、n個のフィールドが得られ、合計実行時間はO（n）になります。
10.2。重複するサブタスクの操作
このセクションで使用されるアプローチは、動的プログラミングと呼ばれます。これは、問題を複数のサブタスクに分割できる場合に使用され、各サブタスクのソリューションは複数回使用されます。このアプローチは、問題が互いに独立して解決されるサブタスクに分割される「分割と征服」の原則とは異なります。チェス盤の問題では、各サブ問題は他の3つの問題の解決策に依存し、すべてのサブ問題の解決策はさらに使用するために保存されました。
動的プログラミングは通常、上記のようにテーブルを作成することによって行われます。これは、ボトムアップアプローチを使用して問題を解決することを意味します。このアプローチでは、最小のサブ問題を解決することから始めて、答えが得られるまで作業を進めていきます。もう1つの方法は、メモ化です。この方法では、上から下に移動し、必要に応じてサブ問題を解決し、結果をキャッシュして再利用します。この方法のコストはメモ化よりも少ないため、各サブ問題を解決する必要がある場合（チェスボードを使用した私の例では、ボードの各フィールドに対して最大の無傷の領域を見つける必要がありました）、テーブルの作成が推奨されるオプションです。ソリューション領域の一部のサブタスクを解決する必要がない場合、メモ化により、本当に必要なサブタスクのみを解決できます。
キーポイント
分割と征服がタスクをいくつかの独立したサブタスクに分割することを含む場合、動的プログラミングはタスクをいくつかの重複するサブタスクに分割することを意味します。各サブ問題の解決策は、後で再利用できるようにキャッシュされます。
10.3。動的プログラミングと最短パス
最短パスを見つける問題を考えてみましょう。重み付きエッジを持つ特定のグラフについて、コストが最も低いノードから別のノードへのパスを見つける必要があります。
定義
エッジ加重グラフは、各エッジに独自の重み（コスト）があるグラフです。あるノードから別のノードへのパスのコストは、トラバースされたすべてのエッジのコストの合計によって決定されます。
3番目のノードvを含むノードsとtの間のパスを見つけたとします。次に、sからtへのパスには、sからvへの最短パスが含まれている必要があります。そうしないと、このセグメントをより短いパスに置き換えて、最短パスの長さをsからtに短縮でき、初期条件と矛盾します（これはベルマンの最適性の原則です）。
( ) , . , . , .
, , .
下部構造の最適なプロパティが直感的に明確であるため、最短パスを見つける問題は動的プログラミングの印象的な例です-ポイントAからポイントCにポイントBを経由して移動する最速の方法は、ポイントAからポイントBに移動する最速の方法でもあることは明らかです。 BからポイントCまで。この原則に基づくアルゴリズムの数には、開始点からグラフの任意の頂点まで（またはグラフの任意の頂点から終了点まで）の最短パスを見つけるBellman-FordメソッドとFloyd-Warshallメソッドが含まれます。グラフ頂点の各ペア間の最短パスが計算されます。どちらの場合も、対象のノードに近いノードの小さなサブセットから開始し、すでに見つかったノードを使用してこのセットを徐々に拡張して、新しい距離を計算するという考え方です。
10.4.
10.4.1. Git merge
動的プログラミングを示すために一般的に使用される別のタスクは、最長の共通サブシーケンスを見つけることです。タスクは、2つの指定された文字列AとBについて、文字のシーケンスを維持しながら、両方の文字列で発生する最長のシーケンスを見つけることです。文字列は一列に並んでいる必要はありません。たとえば、A = {acdbef}およびB = {babdef}の場合、{adef}がそれらの共通のサブシーケンスになります。
Gitの変更をマージ（マージ）するとき、マスターブランチと作業ブランチの最大の共通サブシーケンスを検索します。マスターには存在するが、最大の共通サブシーケンスには存在しない文字は削除されます。作業ブランチにはあるがこのサブシーケンスにはない文字がマスターに追加されます。
10.4.2. LATEX
LATEXドキュメント準備システムは、技術ドキュメントの作成によく使用されます。タイピングシステムのタスクの1つは、テキストを同時に左右に揃えることです。これを行うには、すべての行が同じ長さになるように、単語と文字の間のスペースを拡大または縮小します。テキストを揃えるもう1つの方法は、最後の単語を折り返して、単語の一部が次の行に表示されるようにすることです。 LATEX（技術的な観点から、ほとんどすべての作業はTEXテキスト入力システムによって行われます。LATEXはTEXの上に構築されます。ここでは、簡単にするためにLATEXを使用します）は、テキストの見栄えを良くするために最適な改行ポイントを見つけようとします。これが失敗した場合、行の複数の行が単語のハイフンで終わるか、異なる行の単語間の距離が異なります。LATEXには、アライメントの失敗を評価するための一連のルールがあります。プログラムは、「最も悪い」オプションを見つけようとします。
段落にn個の可能な改行ポイントが
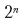ある場合、テキストを分割するための可能なオプションがあります。各ブレークポイントの選択の「失敗」は、その前に選択されたブレークポイントによって異なります。したがって、サブタスクが重複しています。動的プログラミング手法を使用すると、実行時間が短縮
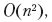され、追加の方法で改善できます。
»本の詳細については、出版社のWebサイトを参照してください
»目次
» 住民向けの抜粋
クーポンの25％割引-コンピューターサイエンス
本の紙版の支払い時に、電子書籍が電子メールに送信されます。