四面体方程式の解は、コンピューター検索の数十年後に証明されています

4人の数学者が、数論法を使用して有理数の四面体の完全なリストを作成することにより、基本的な幾何学的形状の問題をどのように解決したか。

有理二面角を持つ59個の四面体はすべて、参照によりさまざまな側面から見ることができます 。



四面体は、側面が平らな最も単純な3次元形状です。その主な特性は、プラトンとアリストテレスの時代でさえ、好奇心旺盛な心を困惑させてきました。そして2020年11月に、既存のすべての特殊な四面体を確実に識別する最終的な証明が公開されました 。この作品では、数学者は、特定の方程式の解を見つける新しい方法を使用できるようにする高度な技術のおかげで、古代の人物の質問に答えています。



「これらは常に私たちと一緒にいる理想的な数学的対象であり、今ではそれらすべてを知っています」とカリフォルニア大学サンタクルーズ校のマーティン・ワイスマンは言い ます。



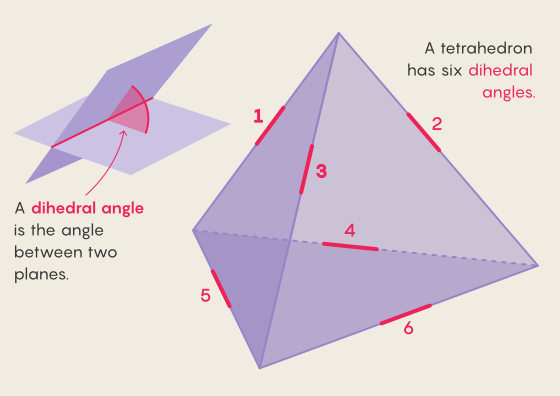
四面体は、三角形の底面と3つの三角形の辺を持ち、ピラミッドを形成します。面のペアがエッジに沿って接触し、6つの二面角を形成します。



新しい証明は、四面体の構成のすべてのバリエーションを定義します。ここで、6つの二面角のそれぞれは有理数を持ちます。つまり、それぞれが分数として記述できます。この条件を満たす、正確に59の個別の例と、2つの無限の四面体ファミリーがあると記載されています。



実際、これらの四面体は数十年前にコンピューター検索方法を使用して数学者によって発見されましたが、他にあるかどうかはわかりませんでした。もっと広く言えば、彼らは他に同様の四面体がないことを証明する方法を理解していませんでした。



「それらは1990年代に発見されましたが、リストが包括的であることを証明できたのは2020年まででした」とカリフォルニア大学サンディエゴ校の数学者であるキランケドラヤは述べてい ます。ケドラヤは、スイスのヌーシャテル大学の アレクサンダーコルパコフ、マサチューセッツ工科大学のビョルンプネン、マイケルルービンスタインと の証明の共著者です。 ウォータールー大学から。





Samuel Velasco / Quanta Magazine



有理二面角で四面体を分類する問題は単純に思えるかもしれませんが、それを解決するには数年の蓄積された数学的知識と、10年前でも利用できなかった計算能力が必要でした。



「ペンと紙で遊んだだけでは、そのような結果は得られません。彼らは非常に洗練された方法を開発しました」とスミス大学のMarjorieSeneschalは言い ます。



30ページのプルーフにはほとんど図面がありません。代わりに、ロジックは、係数と変数が累乗される多項式を解くことに基づいています。たとえば、y = 3x ²+ 6.もちろん、証明で考慮される方程式ははるかに複雑です。



「ほとんどの作業は数論に基づいていますが、幾何学は表面にあります」とケドラヤは言います。



幾何学と数論の関係は数学者に手がかりを与えましたが、複雑な方程式の特別な解を見つけてそれらすべてを見つけたことを証明することは非常に難しいため、数学者はこのアイデアを開発するために一生懸命努力しなければなりませんでした。数学者は、ほとんどの方程式でこれを行う方法を知りません。



「常に機能する万能の方法はありません。方程式を解くことはほとんど不可能です」と高等研究所のピーター・サルナックは言い ます。



この場合のみ、数学者は成功しました！彼らは、多項式の解を見つけるための新しい方法を発見することで、幾何学的形状に関する基本的な質問に答え、将来的に他の方程式の解を見つけるのを容易にしたかもしれません。

四面体のテスト

有理二面角ですべての四面体を定義する問題（有理四面体）は、 1976年の論文でジョンコンウェイとアントニアジョーンズによって最初に正式に定式化されまし た。



彼らは、同じ体積の立方体に切断して組み立てることができる四面体を見つけたいと考えていました。これは、はさみの合同として知られている特性です。彼らの研究では、DavidHilbertが20世紀の数学的研究を導く23の問題を提案した1900年にさかのぼって推論を展開しました。彼の3番目の問題は、次の質問に関連しています。等量のはさみの3次元図形のペアです。これが当てはまらないことがすぐに証明されましたが、すべての有理四面体が立方体に合同であることが判明しました。



「コンウェイとジョーンズは、四面体の分類のはるかに複雑な問題の特別な場合として、合理的な四面体の質問をしました」とケドラヤは言いました。

これらは、常に私たちと一緒にいる理想的な数学的対象です。



マーティンワイスマン、カリフォルニア大学サンタクルーズ校。

彼らは、これらの四面体を見つける方法、つまり特定の多項式を解く方法をスケッチすることができました。それらの方程式には、四面体の6つの二面角に対応する6つの変数が含まれ、四面体の二面角の相互の複雑な関係を反映する105の項があります。比較のために、三角形を想像してみてください。その3つの内角は、a + b + c = 180度の3つのメンバーのみで構成される単純な多項式内で接続されています。



ConwayとJonesによって特定された多項式には、可能な四面体の無限構成に対応する無限に多くの解もあります。コンウェイとジョーンズは、すべての有理二面角で四面体を定義するために、数学者は有理四面体に正確に対応する方程式の特別なクラスの解を見つける必要があると述べました。



彼ら自身は解決策を見つける方法を知りませんでしたが、それができると確信していました。「二面角が有理数である通常の四面体は、私たちの方法を使用して見つけることができる可能性があります。」



40年以上後、4人の数学者が彼らの仮定を確認しました。

1つのルーツ

コンウェイとジョーンズの戦略は、多項式を研究するときに特別なタイプの解を探すことが多い数学者の間で非常に一般的です。これらは、整数または有理数の形式の解にすることができます。または、この場合のように、「1つのルーツ」というエレガントな名前のソリューションにすることもできます。



1つの根のほとんどは、通常の数直線には表示されません。代わりに、それらは3 + 4iのような複素数の中にあり、実数部（3）と虚数部（4）があります。単一性の根は、多項式の解として機能し、特別な代数的特性を持っています。それらを特定のべき乗に上げると、1が得られます。さらに、それらはエレガントな幾何学的表現を持ちます。それらはすべて、複素平面の単位円上にあります。



Conway-Jones多項式を解くには、6つの変数すべてに複素数を割り当てて、105項の方程式を真にする必要があります。変数は文字通り実際の角度測定値を表すものではありませんが、角度の余弦定理に関連付けられた複素数を置き換えます。 ConwayとJonesは、有理四面体がすべての変数が1の根である多項式の解に対応することに気づきました。



「6つの角度は単位円上の6つの点になり、これらの複素数は多項式を満足させるために必要です」とワイスマン氏は述べています。





サミュエルベラスコ/クアンタマガジン



ただし、この対応を知ることは、思ったほど役に立ちません。解決策を見つけることは1つのことです。そして、それらすべてを見つけたことを証明することは、まったく異なり、はるかに難しい作業です。



1995年、新作の2人の著者、PunenとRubinsteinは、最終的に判明したように、実際にはすべての四面体を有理二面角で見つけました。実際、彼らは6つの有理数の組み合わせを方程式に代入することによってそれらを見つける方法を推測しました。



「6つの有理数を取り、それらを方程式に代入することを試みることができます」とプーネンは言いました。「問題は、この方法では解決策しか見つけられないことです。しかし、彼はすべての可能な選択肢が見つかったかどうかを明らかにしていません。」

すべてのソリューションを検索する

彼らの新しい研究で、4人の数学者は、25年前にPunenとRubinsteinによって発見された有理数の四面体のリストが完全であり、他の例が発見されないことを証明しました。



彼らのコラボレーションは、プーネンが別の数学者によって共同執筆されたケドライの関連する仕事についてのある講演で聞いた後、2020年3月に始まりました。彼らは、別の分類問題を解決するために、別の多項式の単位から根を探しました。 Poonenは、これが彼の以前の未完成の四面体の研究と関係があることにすぐに気づきました。



「ビョルンは私の仕事に非常に興味を持っていました」とケドレイは言いました。 「彼は言った、 『待って、それはまさに1990年代に私が必要としていたものだ』。



Bjorn Punenは、有理四面体を見つける問題を説明する手紙をKiranKedlaeに書きました。彼の短い手紙は楽観的なメモで終わった。 「私は1990年代に[MichaelRubinsteinと共に]この問題についてかなり遠いところに行きました、そしてそれは多くの人間とコンピューターの努力で完了することができると思います。





2020年、キラン・ケドラヤ、マイケル・ルビンスタイン、ビョルン・プネン、アレクサンダー・コルパコフは方程式を解く新しい方法を発明し、そうすることですべての有理四面体を見つけました。



この手紙の後、ケドライはコルパコフに目を向けました。コルパコフはまた、統一からのルーツを使用して幾何学的形状のタイプを分類しました。同時に、プーネンは当時の共著者であるルービンスタインに連絡を取りました。チームを作った後、彼らはすぐに仕事に取り掛かりました。



「私たちはかなり定期的な会議を開催しました。おそらく週に2時間、数か月間です」とケドラヤは言いました。そして、彼らがコンウェイ-ジョーンズ多項式の統一のルーツの完全なリストを編集し始めたとき、彼らはそれらを探す場所について非常に幅広い考えを持っていました。



彼らは、解が非常に大きな数、つまり上限を下回らなければならないことを知っていました。しかし、国境はとても素晴らしかったので、その下のすべての可能性を探求することに疑問の余地はありませんでした。



「これらの6つの変数の境界は恐ろしいものです。根本的に新しいアイデアがなければ、この問題の解決策は可能性の範囲を超えています」とSarnak氏は述べています。



4人の数学者が、2つの主要な革新を通じて方程式を解けるようにしました。



まず、彼らは上限を下げました。彼らの新しい論文では、四面体を表す1つの複素多項式は、それ自体がいくつかのより単純な多項式として表すことができることを証明しました。



「私たちは、6つの変数を持つ1つの方程式から、何百ものより単純な方程式のセットに移行しています」とケドラヤは言いました。



彼らは、これらのより単純な多項式の1のすべての根が上限の下にあることを証明しました。上限は、より複雑な多項式に関連する広大で未踏の上限よりもはるかに小さいものです。より単純な方程式と複雑な方程式の対応は、前者の1つの根を見つけると、後者の1の根が得られることを意味します。残念ながら、この短い間隔でさえ、すべての可能なオプションを検討するには長すぎました。

ペンと紙で遊んだだけでは、この結果は得られません。



スミス大学、マージョリー・セネシャル

著者の2番目の革新は、この短い間隔で検索する巧妙な方法の開発にありました。彼らは、解が特定の対称構造を持っていることを知っていました。つまり、区間の一部に解がある場合、区間の他の部分にも解がなければなりません。



これにより、この構造を使用してより効率的に検索する新しいアルゴリズムを開発することができました。さらに、問題を解決するために1からの根を使用することを最初に提案したとき、ConwayとJonesが持っていたよりもはるかに強力なコンピューターでこれらのアルゴリズムを使用しました。



「40年の追加知識とより強力なコンピューターを使用して、[コンウェイとジョーンズの]戦略を少し再設計する必要があったことがわかりました」とケドレイ氏は述べています。



新しいアルゴリズムは、より狭い間隔でソリューションのすべての可能な組み合わせをテストしました。この徹底的な決定的な検索に基づいて、著者は最終的に、有理二面角を持つ四面体の59の別々の例と、四面体の2つの無限のファミリー（正確には、プネンとルビンスタインが数十年前に遭遇したもの）があることを証明しました。各無限ファミリの四面体は1つのパラメータが異なり、すべての二面角を合理的に保ちながら、一部の角度のサイズを大きくしたり、他の角度を小さくしたりするための無限のオプションを提供します。



この探索では、誰もが自分のために何かを見つけるでしょう。



多項式の単位の根を特定することに関心のある数学者のために、この記事はそれらを見つけるための新しい便利な方法を提供します。特に、著者が複雑なConway-Jones多項式をより単純な多項式に還元するために使用した方法は、直接解くことのできない他の複雑な多項式に適用される可能性があります。



「この作業は、克服できないと思われた他の多くの問題が、そのようなアイデアで解決できる可能性があることを示唆しています」とSarnak氏は述べています。



そして、それらの数学者や完全性が好きな他のすべての人のために、この記事は新しく完璧な答えを提供します：ここにあなたが夢見ることしかできないすべての四面体があります。



「これは素晴らしい成果です」とSarnak氏は述べています。