
Armored Warfare:Project Armataは、ゲームスタジオMY.GAMESのAllods Teamが開発した無料のオンライン戦車ベースのアクションゲームです。ゲームはリアルタイムレンダリングが優れたかなり人気のあるエンジンであるCryEngineで作成されていますが、このゲームでは、多くの部分を最初から変更して作成する必要があります。この記事では、一人称視点で色収差をどのように実装したか、そしてそれが何であるかについてお話したいと思います。
色収差とは何ですか?
色収差は、すべての色が同じ点に到達するわけではないレンズの欠陥です。これは、媒質の屈折率が光の波長に依存するためです(分散を参照)。たとえば、レンズに色収差がない場合の状況は次のとおりです。
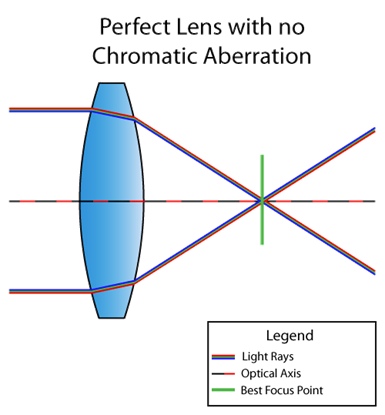
そしてここに欠陥のあるレンズがあります:
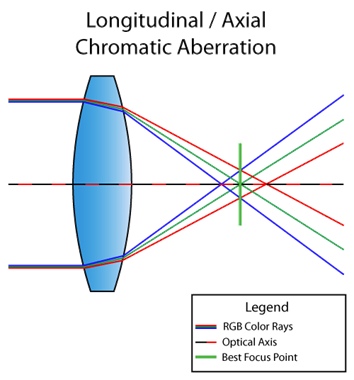
ちなみに、上記の状況は縦(または軸)色収差と呼ばれています。これは、レンズを通過した後、異なる波長が焦点面の同じ点に収束しない場合に発生します。次に、欠陥が全体像に表示されます。

上の写真では、欠陥のために紫と緑の色が際立っています。見ることができません?そして、この写真では?

また、横(または横)の色収差もあります。光がレンズに対して斜めに入射すると発生します。その結果、異なる波長の光が焦点面の異なる点に集束します。ここにあなたが理解するための写真があります:
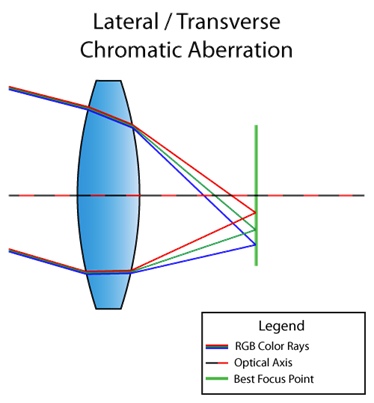
図から、結果として赤から紫に光が完全に分解されていることがわかります。縦方向とは異なり、倍率色収差は中央に表示されることはなく、画像の端にのみ表示されます。あなたが私の意味を理解できるように、ここにインターネットからの別の写真があります:

さて、私たちは理論を終えたので、要点に行きましょう。
光分解を伴う側方色収差
多くの皆さんの頭の中で起こり得る質問に答えるという事実から始めましょう:「CryEngineは色収差を実装していませんか?」有る。しかし、それはシャープ化と同じシェーダーの後処理段階で使用され、アルゴリズムは次のようになります(コードへのリンク)。
screenColor.r = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 + 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).r;
screenColor.b = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 - 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).b;これは、原則として機能します。しかし、戦車に関するゲームがあります。この効果は、一人称視点でのみ、そして美しさでのみ必要です。つまり、すべてが中心に焦点を合わせています(こんにちは横収差)。したがって、現在の実装は、少なくともその効果が全体にわたって見えるという事実には適していません。
これは、収差自体がどのように見えるかです(左側に注意)。

そして、これはパラメーターをひねった場合の外観です。

したがって、私たちは目標として設定しました:
- 倍率色収差を実装して、すべてがスコープの近くに焦点が合うようにし、特徴的な色の欠陥が側面に見えない場合は、少なくともぼかします。
- RGBチャネルに特定の波長に対応する係数を掛けて、テクスチャをサンプリングします。これについてはまだ話していないので、この点が何であるかが完全に明確になっていない可能性があります。ただし、後で詳しく説明します。
最初に、倍率色収差を作成するための一般的なメカニズムとコードを見てみましょう。
half distanceStrength = pow(length(IN.baseTC - 0.5), falloff);
half2 direction = normalize(IN.baseTC.xy - 0.5);
half2 velocity = direction * blur * distanceStrength;
したがって、最初に、画面の中心からの距離の原因となる円形のマスクが構築され、次に画面の中心からの方向が計算され、次にこれにが乗算され
blurます。Blurそしてfalloff-これらは、外部から渡され、収差を調整するための単なる乗算されているパラメータです。また、外部からパラメータがスローされますsampleCount。これは、サンプル数だけでなく、実際には、サンプリングポイント間のステップにも関与します。
half2 offsetDecrement = velocity * stepMultiplier / half(sampleCount);
今度は
sampleCount、テクスチャの指定されたポイントから一度移動し、毎回をシフトしoffsetDecrement、チャネルに対応する波の重みを乗算し、これらの重みの合計で除算する必要があります。さて、グローバル目標の2つ目のポイントについてお話ししましょう。
光の可視スペクトルは、380 nm(紫)から780 nm(赤)の範囲です。そして見れば、波長はRGBパレットに変換できます。Pythonでは、この魔法を行うコードは次のようになります。
def get_color(waveLength):
if waveLength >= 380 and waveLength < 440:
red = -(waveLength - 440.0) / (440.0 - 380.0)
green = 0.0
blue = 1.0
elif waveLength >= 440 and waveLength < 490:
red = 0.0
green = (waveLength - 440.0) / (490.0 - 440.0)
blue = 1.0
elif waveLength >= 490 and waveLength < 510:
red = 0.0
green = 1.0
blue = -(waveLength - 510.0) / (510.0 - 490.0)
elif waveLength >= 510 and waveLength < 580:
red = (waveLength - 510.0) / (580.0 - 510.0)
green = 1.0
blue = 0.0
elif waveLength >= 580 and waveLength < 645:
red = 1.0
green = -(waveLength - 645.0) / (645.0 - 580.0)
blue = 0.0
elif waveLength >= 645 and waveLength < 781:
red = 1.0
green = 0.0
blue = 0.0
else:
red = 0.0
green = 0.0
blue = 0.0
factor = 0.0
if waveLength >= 380 and waveLength < 420:
factor = 0.3 + 0.7*(waveLength - 380.0) / (420.0 - 380.0)
elif waveLength >= 420 and waveLength < 701:
factor = 1.0
elif waveLength >= 701 and waveLength < 781:
factor = 0.3 + 0.7*(780.0 - waveLength) / (780.0 - 700.0)
gamma = 0.80
R = (red * factor)**gamma if red > 0 else 0
G = (green * factor)**gamma if green > 0 else 0
B = (blue * factor)**gamma if blue > 0 else 0
return R, G, B
その結果、次の色分布が得られます。

つまり、グラフは、特定の長さの波に含まれている色の量と色を示しています。縦軸は、先ほどお話ししたのと同じ重みです。これで、前述のことを考慮して、アルゴリズムを完全に実装できます。
half3 accumulator = (half3) 0;
half2 offset = (half2) 0;
half3 WeightSum = (half3) 0;
half3 Weight = (half3) 0;
half3 color;
half waveLength;
for (int i = 0; i < sampleCount; i++)
{
waveLength = lerp(startWaveLength, endWaveLength, (half)(i) / (sampleCount - 1.0));
Weight.r = GetRedWeight(waveLength);
Weight.g = GetGreenWeight(waveLength);
Weight.b = GetBlueWeight(waveLength);
offset -= offsetDecrement;
color = tex2Dlod(baseMap, half4(IN.baseTC + offset, 0, 0)).rgb;
accumulator.rgb += color.rgb * Weight.rgb;
WeightSum.rgb += Weight.rgb;
}
OUT.Color.rgb = half4(accumulator.rgb / WeightSum.rgb, 1.0);
つまり、の数が多いほど
sampleCount、サンプルポイント間のステップが少なくなり、光を分散することが多くなります(長さが異なる複数の波を考慮に入れます)。
具体的な例では、それはまだ明確でない場合は、してみましょう見て、すなわち私たちの最初の試み、と私はのために取るべき説明します
startWaveLengthとendWaveLength、どのような機能が実装されますGetRed(Green, Blue)Weight。
可視スペクトル全体を当てはめる
したがって、上のグラフから、波長ごとのRGBパレットのおおよその比率とおおよその値がわかります。たとえば、波長が380 nm(紫)の場合(同じグラフを参照)、RGB(0.4、0、0.4)がわかります。先ほどお話しした重みにこれらの値を取り入れています。
次に、4次の多項式で色を取得する機能を取り除いて、計算が安価になるようにしましょう(私たちはPixarスタジオではなく、ゲームスタジオです:計算が安価であるほど優れています)。この4次多項式は、結果のグラフに近似するはずです。多項式を作成するために、SciPyライブラリを使用しました。
wave_arange = numpy.arange(380, 780, 0.001)
red_func = numpy.polynomial.polynomial.Polynomial.fit(wave_arange, red, 4)
その結果、次の結果が得られます(正確な値と比較するのが簡単になるように、各個別のチャネルに対応する3つの個別のグラフに分割します)。
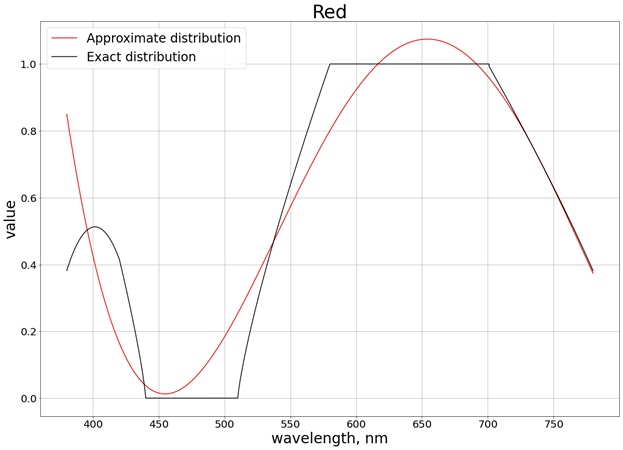
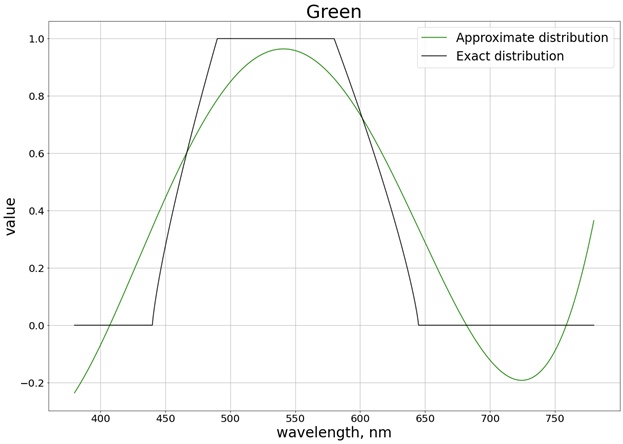
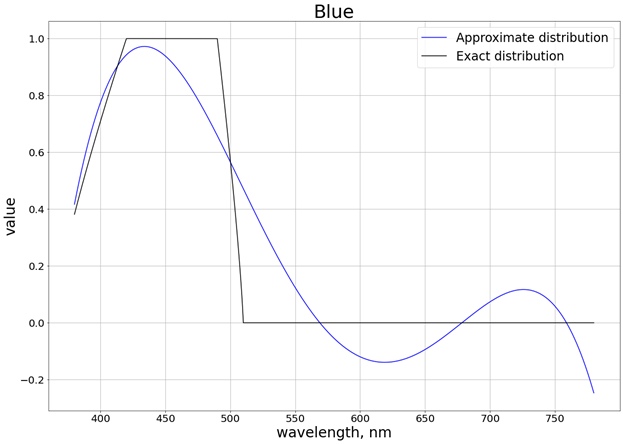
値がセグメント[0、1]の制限を超えないようにするために、関数を使用します
saturate。たとえば赤の場合、関数は次のように取得されます。
half GetRedWeight(half x)
{
return saturate(0.8004883122689207 +
1.3673160565954385 * (-2.9000047500568042 + 0.005000012500149485 * x) -
1.244631137356407 * pow(-2.9000047500568042 + 0.005000012500149485 * x, 2) - 1.6053230172845554 * pow(-2.9000047500568042 + 0.005000012500149485*x, 3)+ 1.055933936470091 * pow(-2.9000047500568042 + 0.005000012500149485*x, 4));
}
行方不明のパラメータ
startWaveLengthとendWaveLength、この場合には、それぞれ、780 nmおよび380 nmです。実際の結果sampleCount=3は次のとおりです(図の端を参照)。

値を調整し
sampleCountて400に増やすと、すべてが良くなります。

残念ながら、1つのシェーダーで400サンプル(約3〜4)を許可できないリアルタイムレンダリングがあります。したがって、波長範囲をわずかに狭めました。
可視スペクトルの一部
純粋な赤と純粋な青の両方の色になるように範囲を考えてみましょう。また、左側の赤い尾は、最終的な多項式に大きく影響するため、拒否します。その結果、セグメント[440、670]の分布が得られます。

また、値が変化するセグメントについてのみ多項式を取得できるようになったため、セグメント全体を補間する必要はありません。たとえば、赤い色の場合、これはセグメント[510、580]であり、重みの値は0から1まで変化します。この場合、2次多項式を取得できます。これは
saturate、関数によって値の範囲[0、1]にも削減されます。3つの色すべてについて、彩度を考慮した次の結果が得られます。

その結果、たとえば、次の赤の多項式が得られます。
half GetRedWeight(half x)
{
return saturate(0.5764348105166407 +
0.4761860550080825 * (-15.571636738012254 + 0.0285718367412005 * x) -
0.06265740390367036 * pow(-15.571636738012254 + 0.0285718367412005 * x, 2));
}
そして実際には
sampleCount=3:

この場合、ツイスト設定を使用すると、可視スペクトルの全範囲にわたってサンプリングする場合とほぼ同じ結果が得られます。

したがって、2次の多項式では、440 nmから670 nmの波長範囲で良好な結果が得られました。
最適化
多項式による計算を最適化することに加えて、横方向の色収差に基づいて作成したメカニズムに依存して、シェーダーの作業を最適化できます。つまり、総変位が現在のピクセルを超えない領域で計算を実行しないでください。そうでない場合は、同じサンプルをサンプリングしますピクセル、それを取得します。
次のようになります。
bool isNotAberrated = abs(offsetDecrement.x * g_VS_ScreenSize.x) < 1.0 && abs(offsetDecrement.y * g_VS_ScreenSize.y) < 1.0;
if (isNotAberrated)
{
OUT.Color.rgb = tex2Dlod(baseMap, half4(IN.baseTC, 0, 0)).rgb;
return OUT;
}
最適化は小規模ですが、非常に誇りに思っています。
結論
倍率色収差自体は非常にクールに見えます。この欠陥は中央の視界を妨げません。ライトをウェイトに分解するというアイデアは、非常に興味深い実験であり、エンジンまたはゲームで4つ以上のサンプルが許可されている場合、まったく異なる画像を提供できます。私たちの場合、最適化を行っても多くのサンプルを用意することはできず、たとえば3と5のサンプルの違いがあまり見えないため、わざわざ別のアルゴリズムを考え出すことはできませんでした。説明した方法を自分で試して、結果を確認できます。