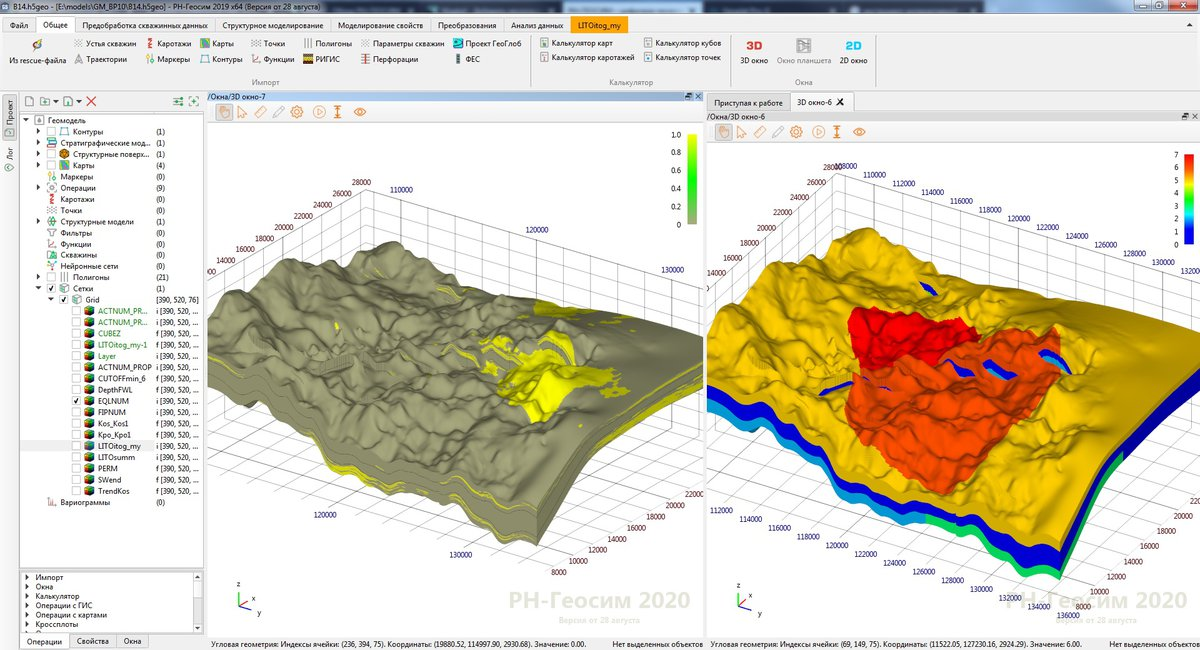
これは、数学が最初に地質学に侵入した方法、その後ITスペシャリストが来てすべてをプログラムし、それによって「デジタル地質学者」の新しい職業を生み出した方法についての物語の始まりです。これは、確率的モデリングがクリギングとどのように異なるかについての話です。また、最初の地質学的ソフトウェアを自分で作成し、おそらく、地質学的および石油工学産業を何らかの形で変革する方法を示す試みでもあります。
オイルの量を計算してみましょう
, , , , . , , . , (, ). , , , .
— , , , , , , , .
, — . , — . — . , ( , , ) . . , , ( , , ).
. , , , , . — , , . — , , , . , , .
. ; , , , .
, , . , , , , . , .
, , , . , , . , . . , , , - , .
, — , .
, , .. , , . , , , . — — «support». , , , , . .
, , (Krige, D.G. 1951. A statistical approach to some basic mine valuation problems on the Witwatersrand. Journal of the Chemical, Metallurgical and Mining Society of South Africa, December 1951. pp. 119–139.). , -, , , , . , , 5×5 , , , 1 , 50 ×50 ×1 — , , ( — upscaling).
. , — . .
. ,
.
— , . , . , , , .
:
— . (. . 1). , . , . , . , , 1, , .
Python .
import numpy as np
import matplotlib.pyplot as pl
# num of data
N = 5
np.random.seed(0)
# source data
z = np.random.rand(N)
u = np.random.rand(N)
x = np.linspace(0, 1, 100)
y = np.zeros_like(x)
# norm weights
w = np.zeros_like(x)
# power
m = 2
# interpolation
for i in range(N):
y += z[i] * 1 / np.abs(u[i] - x) ** m
w += 1 / np.abs(u[i] - x) ** m
# normalization
y /= w
# add source data
x = np.concatenate((x, u))
y = np.concatenate((y, z))
order = x.argsort()
x = x[order]
y = y[order]
# draw graph
pl.figure()
pl.scatter(u, z)
pl.plot(x, y)
pl.show()
pl.close()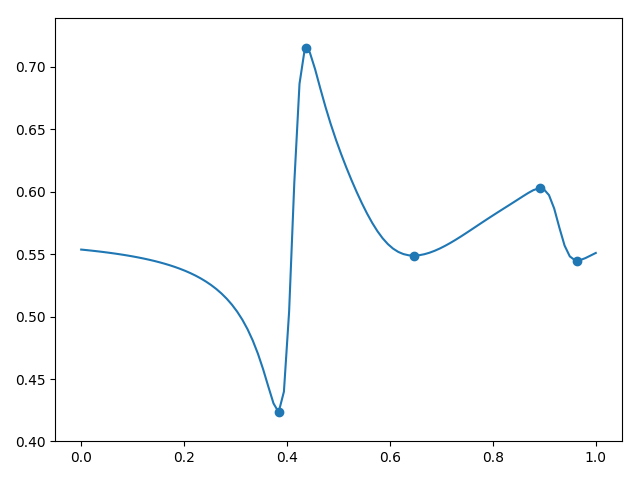
1.
. , , - . , , . -, , , , ? , . , 1 . , , . , , (. . 2). .

2.
, , , , . , , . , . — , , : , , , . , .
(2) :
, , . , , - - . .
, :
- , — . (4) — «», . . , (1):
. , — , — , — «» . , , (6),
(6) ( ). (4) , , dual kriging. (6) (3), , . , (7) , , , , ( ).
(. . 3). , , .
, — Python:
import numpy as np
import matplotlib.pyplot as pl
# num of data
N = 5
np.random.seed(0)
# source data
z = np.random.rand(N) - 0.5
u = np.random.rand(N)
x = np.linspace(0, 1, 100)
y = np.zeros_like(x)
# covariance function
def c(h):
return np.exp(-np.abs(h ** 2 * 20.))
# covariance matrix
C = np.zeros((N, N))
for i in range(N):
C[i, :] = c(u - u[i])
# dual kriging weights
lamda = np.linalg.solve(C, z)
# interpolation
for i in range(N):
y += lamda[i] * c(u[i] - x)
# add source data
x = np.concatenate((x, u))
y = np.concatenate((y, z))
order = x.argsort()
x = x[order]
y = y[order]
# draw graph
pl.figure()
pl.scatter(u, z)
pl.plot(x, y)
pl.show()
pl.close()
3.
, , . (5) (6) , .
, , . , , , .
. , (), , , , . , «», . , (6), , «», . , «» . : . , , , — . , , .
. , . . , , .
.
from theory import probability
from numpy import linalg, , .
, . () : u , ( ). , .
. . , ( , ).
, - — . - , . : — ( ), , , , . — , .
( , ) . — . , u , .
, , : . -, — «» (4), : . , , .., , , .
, , , , . , , . , , . .
, ( ). :
, , , , . . , , , ( ) , , . . .
, ( , , — , ). , (. . 4).
import numpy as np
import matplotlib.pyplot as pl
np.random.seed(0)
# source data
N = 100
x = np.linspace(0, 1, 100)
# covariance function
def c(h):
return np.exp(-np.abs(h ** 2 * 250))
# covariance matrix
C = np.zeros((N, N))
for i in range(N):
C[i, :] = c(x - x[i])
# eigen decomposition
w, v = np.linalg.eig(C)
A = v @ np.diag(w ** 0.5)
# you can check, that C == A @ A.T
# independent normal values
zeta = np.random.randn(N)
# dependent multinormal values
Z = A @ zeta
# draw graph
pl.figure()
pl.plot(x, Z)
pl.show()
pl.close()
4.
, , ( , ). , 5.
import numpy as np
import matplotlib.pyplot as pl
np.random.seed(3)
# source data
M = 5
# coordinates of source data
u = np.random.rand(M)
# source data
z = np.random.randn(M)
# Modeling mesh
N = 100
x = np.linspace(0, 1, N)
# covariance function
def c(h):
return np.exp(−np.abs(h ∗∗ 2 ∗ 250))
# covariance matrix mesh−mesh
Cyy = np.zeros ((N, N))
for i in range (N):
Cyy[ i , : ] = c(x − x[i])
# covariance matrix mesh−data
Cyz = np.zeros ((N, M))
# covariance matrix data−data
Czz = np.zeros ((M, M))
for j in range (M):
Cyz [:, j] = c(x − u[j])
Czz [:, j] = c(u − u[j])
# posterior covariance
Cpost = Cyy − Cyz @ np.linalg.inv(Czz) @ Cyz.T
# lets find the posterior mean, i.e. Kriging interpolation
lamda = np.linalg.solve (Czz, z)
y = np.zeros_like(x)
# interpolation
for i in range (M):
y += lamda[i] ∗ c(u[i] − x)
# eigen decomposition
w, v = np.linalg.eig(Cpost)
A = v @ np.diag (w ∗∗ 0.5)
# you can check, that Cpost == A@A.T
# draw graph
pl.figure()
for k in range (5):
# independent normal values
zeta = np.random.randn(N)
# dependent multinormal values
Z = A @ zeta
pl.plot(x, Z + y, color=[(5 − k) / 5] ∗ 3)
pl.plot(x, Z + y, color=[(5 − k) / 5] ∗ 3, label=’Stochastic realizations’)
pl.plot(x, y, ’. ’, color=’blue’, alpha=0.4, label=’Expectation(Kriging)’)
pl.scatter(u, z, color=’red ’, label=’Source data’)
pl.legend()
pl.show()
pl.close()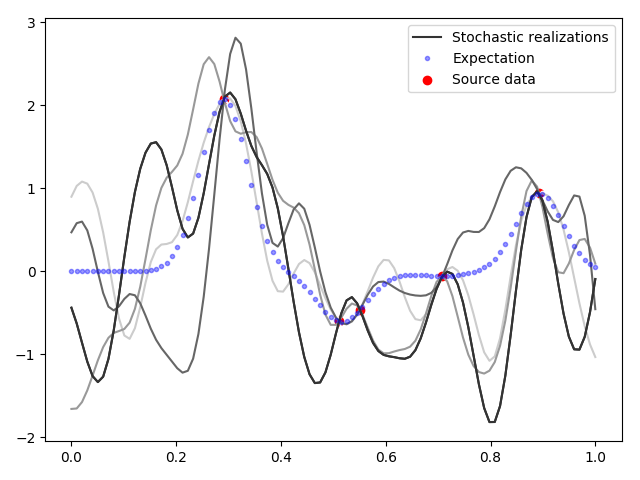
5.
5, . , , , , ( ). , , . — .
, , , (6). , , ( , , ).
, . , . . , , , — . , . — . , - 22 — . -5 , — - . , , , !
?
. (2D 3D), ( 1D ), , , numpy .
, , 6 «» -.
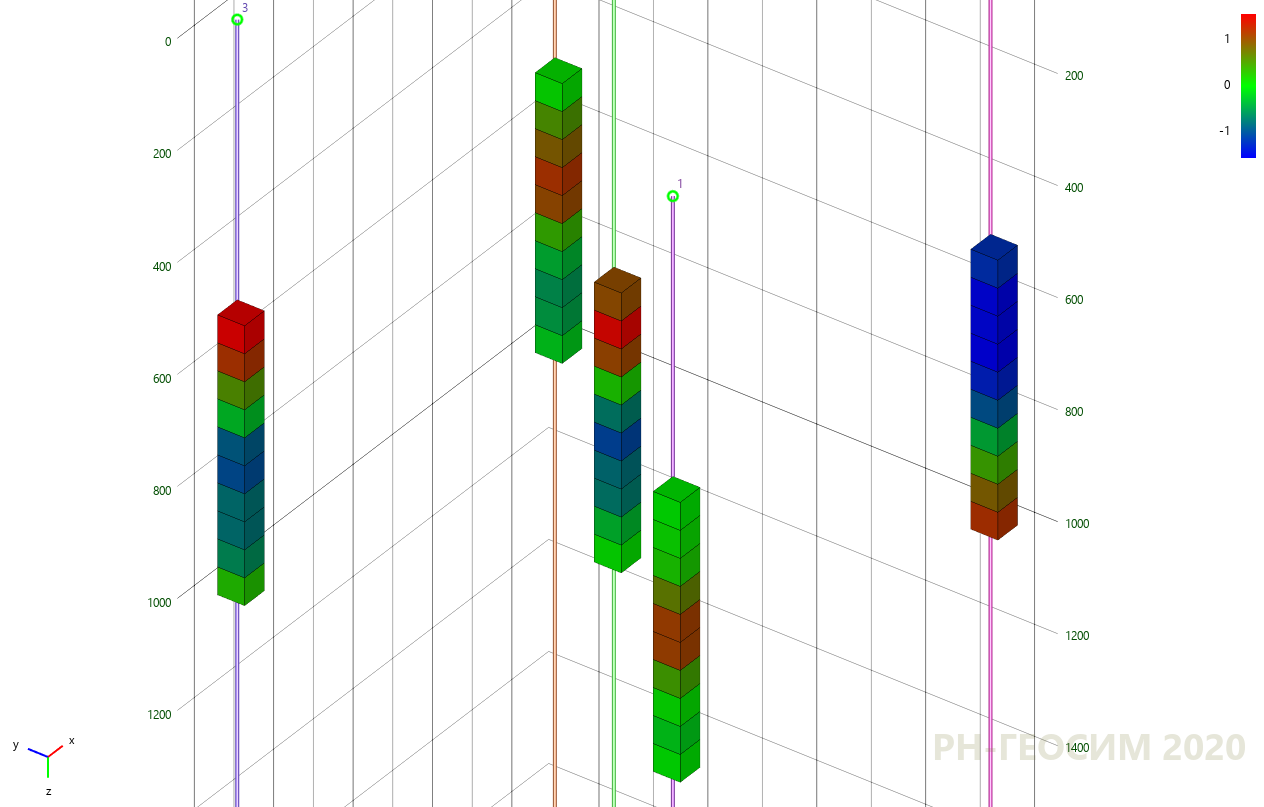
6. «» -
« ». , . (« ») (. 7) (. 8).
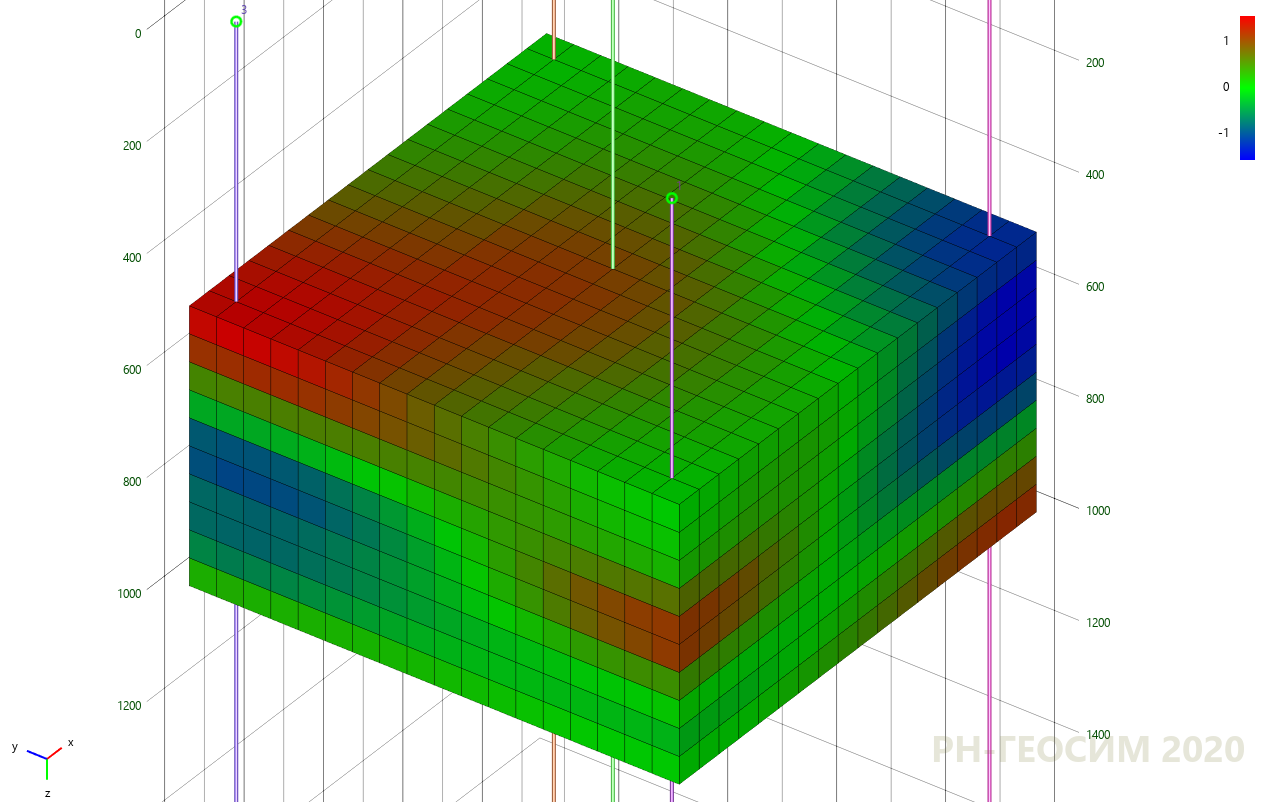
7. «» -

8. «» -
7 8 «» , , , «» .
«»
, . , «X» «Y», . 9.
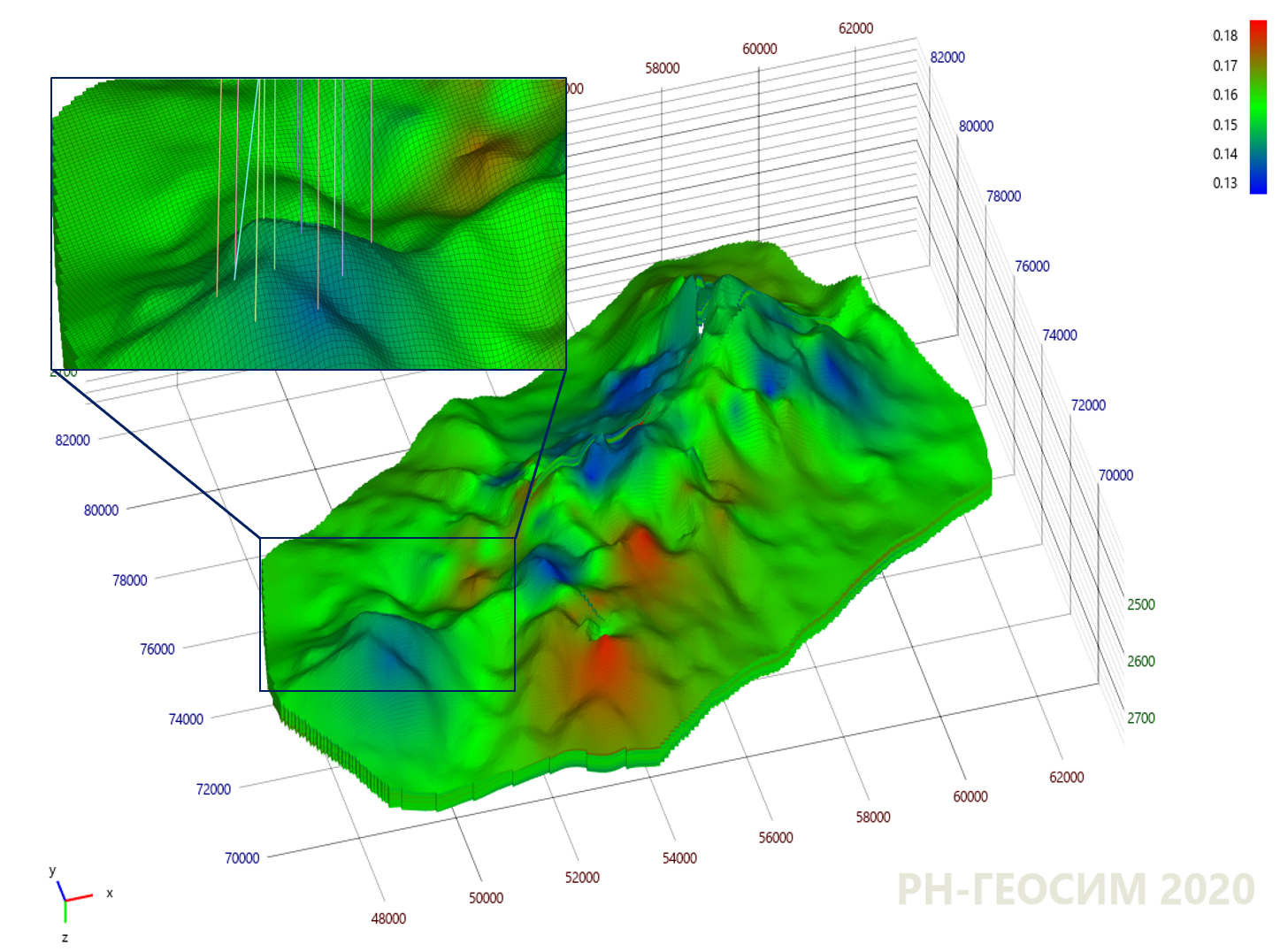
9. "X"
, . , , — ( ). (. . 10).

10. "X"
10 , , - .
, . . , . , .
, , , () , . . ( ), . . , ? , , , :
- ;
- ;
- , .
, - , , , , , , .