-みなさん、こんにちは。私の名前はリシャットです。Yandex検索の品質に約3年間取り組んできました。でも、今日は仕事についてではなく、自由な時間に何をしているのかを話したいと思います。私は量子情報学に携わっていますが、実際には、量子モデルを含むさまざまな計算モデルがあります。
量子情報学は現在興味深い分野です。そこでは多くの努力が注がれ、多くのことが行われました。私の報告では、あなた方の何人かに興味を持ってみるつもりです。たぶん、量子機械学習をやりたいと思っているクールなMLエンジニア、あるいはこの方向に投資できる強力なアルゴリズム論者がいるでしょう。未来がもうすぐ来るのでそれは素晴らしいでしょう。
私は物理学者ではないことをすぐに言わなければなりません。きっと私よりも物理学のすべてのプロセスを理解している人がいるでしょう。したがって、物理学についてはほとんど何も言いません。
代数を少し覚えていること、ベクトルとは何か、ベクトルに行列を乗算する方法を覚えていることを期待します。

レポートはどのように構成されますか?まず、歴史について、自信を持って将来を見据えるためにすべてがどこから来たのかについてお話します。次に、これを適用できる場所、現在の状態、手で何かを実行できるかどうかを確認します。量子コンピューターで実行できる最初のPythonプログラムを作成します。そしておまけとして、量子コンピューティングが古典的なものと比較して比類なく優れたパフォーマンスを達成するのに役立つアルゴリズムの例をいくつか紹介します。

どのようにしてすべてが始まったのですか?この若い男から。これはアランチューリングです。彼は、コンピュータサイエンスまたはコンピュータサイエンスの父と呼ぶことができます。 1930年代に、チューリングは計算プログラムのモデルを思いつきました。これを、現在はプログラム可能なコンピューターと呼んでいます。しかし、誰かがこの人を認識しますか?

より困難。彼の姓は、チューリングの姓の隣に来ることがよくあります。これはアロンツォ教会であり、彼は計算可能性の問題も扱っていました。チューリングが彼自身の計算モデルを思い付く少し前からです。しかし、チューリングの作品はより人気になりました。そして一般的に、教会はある時点でチューリングの科学顧問でした。一緒に取られて、彼らの名前は通常この論文に関連付けられています。
Church-Turingの論文によれば、どのプロセスもTuringマシンで効率的にモデル化できます。これは30代後半から40代前半で、すべてが非常に良好です。この2人が登場するまで、約30年間、すべてが非常に良好でした。誰か知っていますか?

これはすでに70年代で、現在に非常に近いです。それらの姓は、暗号化コースでよく見られます。これらはロバート・ナイチンゲールとフォルカー・ストラッセンです。これらの2人は、数値が単純かどうかをチェックするための確率的アルゴリズム、ソロベリー・ストラセン検定を考案したことで有名です。
これは、私たちにとって非常に重要なポイントです。これまで、チューリングマシンで任意のアルゴリズムプロセスをモデル化できると述べていたからです。しかし今では、そのアルゴリズムをモデル化できないことがわかりました。それは確率論的であり、チューリングマシンにはそのようなものはありません。
私は簡単な修正を行い、どのプロセスも確率論的チューリングマシンでモデル化できると言いました。これはもうあまりクールではありません。確かにあなたの一人があなたの胸をつまんでいます。あなたは思った:どのように?今、私たちは「確率的」と言います。10年後に何かが発見され、何か他のものを修正する必要があります。これはあまり楽しいものではありません。しかし、もちろんあなたと私だけではありません。

別の若者がいました-David Deutsch。そして、彼も不思議に思った:どのように?どうやって暮らしていく?彼はトレーニングによって物理学者であり、彼の人生全体を物理学に捧げました。そして、物理学の観点からこの問題に取り組むことにしました。彼は言った:自然そのものがこれがまさに事実であることを私たちに告げるように、具体化して何かを得ようとしましょう。そして、自然はそのときすでに(そして私たちはまだ信じている)それが量子力学であると言っていました。そこで私たちは量子力学の答えを探し始めました。そして、量子情報学が始まったのは、David Deutschと彼の最初のアルゴリズムでした。
これは歴史への非常に小さな遠足なので、理解できるでしょう。もちろん、この分野には、理論上、実際に問題があり、それを始めた人々を苦しめています。
しかし、すべては理論のレベルでのみですか?概して、数学の観点からは、問題は残っていません。数学的には、量子コンピュータがどのように機能するかについてはすべて知っています。現在、さまざまな方法で動作する、さまざまな構成の実際の量子コンピューターがすでに存在しています。そしてこれは、概して、エンジニアリングの課題です。
たとえば、私たちの研究所には、量子情報学を扱う部門全体があります。数学者と物理学者がいます。物理学者は現在、量子情報の長期保存の問題に非常に密接に取り組んでいます。それは私たちのハードドライブに非常に似ていますが、量子情報をそこに保存したいと考えています。

この経済全体の用途は何ですか?もちろん、最初に頭に浮かぶのはプロセスのモデリングです。これは、世界が量子力学であるためです。また、量子コンピューターを使用してプロセスや化学反応などをシミュレートすると、計算コストが大幅に安くなります。
2番目の非常に大きなセクションは、現在多くの努力が注がれていますが、量子機械学習です。量子コンピューティングが学習プロセス自体のスピードアップとアルゴリズムの改善に役立つことを期待しています。ここには多くの作業があります。たとえば、私たちの量子グループは中国の科学者と協力しています。彼は非常に強力なMLエンジニアであり、私たちは何かを一緒に考え出そうとしていますが、量子バイアスが少しあります。
3番目は、数か月前に少し誇大広告でした。今、誇大広告はすでに眠っていますが、量子ブロックチェーン全体さえあります。それは私の親友と親友によって発明されました。これは私です、少し誇らしげに言います。
しかし、量子コンピューターはありません。残念ながら、Pythonでプログラミングするよりも簡単に家に帰ってプログラムを実行することはできません。
何をすべきか?初学期の論文を書いているとき、3年目にどうするか考えていました。私は量子計算エミュレータを書いていました。もちろん、誰もがエミュレータを作成し、誰もが何らかの形でエミュレータを使用します。 4年目には、干渉やノイズなどをシミュレートするエミュレータを作成しました。そして、私は退屈しました。
検索エンジンで検索してみたところ、エミュレータがたくさんあることに気づきました。ここにいくつかのリンクがあります。それらは非常にシンプルで興味深いものです。
- github.com/quantumlib/Cirq
- github.com/artiste-qb-net/qubiter
- code.google.com/archive/p/pyqu
- qiskit.org
しかし、私はqiskitに立ち寄りたいです。彼は特別で、すべてから際立っています。より?
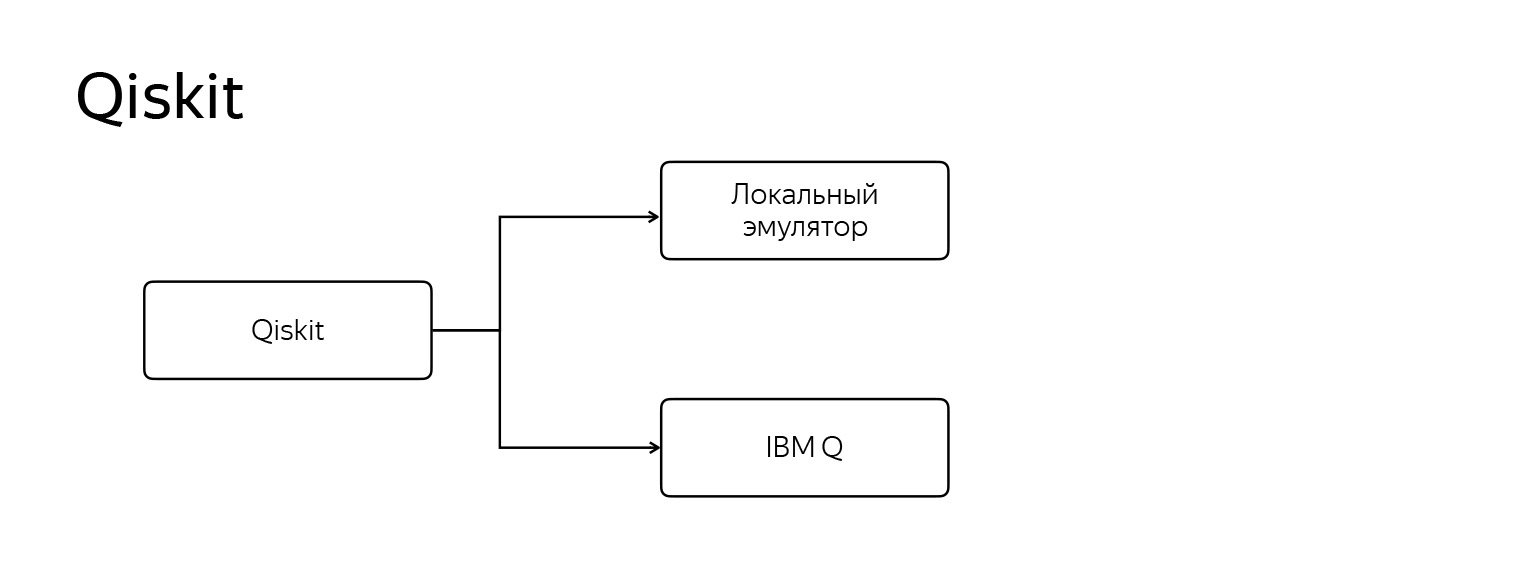
2つのモードで動作します。1つ目は、他の皆と同じように、通常のローカルエミュレータです。2つ目は、このようなプログラムを実際のIBM Q量子コンピューターで実行することです。

今では、非常に低い温度(約3ミリケルビン)が維持される樽全体です。とても寒いです。そしてIBMは、そのマシン上でコードを接続して実行するクラウドベースの機能を提供します。
もちろん、彼はコマンドなどを特別な方法でコンパイルします。それはどのように機能しますか?一般的なアクセスのために、そのようなコンピュータのいくつかのインストールがあります。それらの1つは5キュービットです。15キュービット、16キュービットがあり、20キュービットも利用できます。これは、通常の古典的な情報の約20ビットですが、すでに何かです。
ここでは、確かに、多くの人が考えています。それだけです。欲しいです!しかし、少し数学を覚えておく必要があります。少し代数だが、ほんの少し、私が約束したとおり。
量子コンピューターでプログラミングを開始するには、キュービットとは何かを理解する必要があります。2次元ベクトル空間の単なるベクトルです。しかし、ここではベクトル空間について話しているので、それらには基礎があります。

基本はこんな感じです。2つのベクトル列と単位基底、標準があり、代数コースでは次のように表されます。
そして
...そして、ディラックの表記には、これらの山括弧内に標準表記があります。
つまり、混乱しないように、このように短くしていきます。
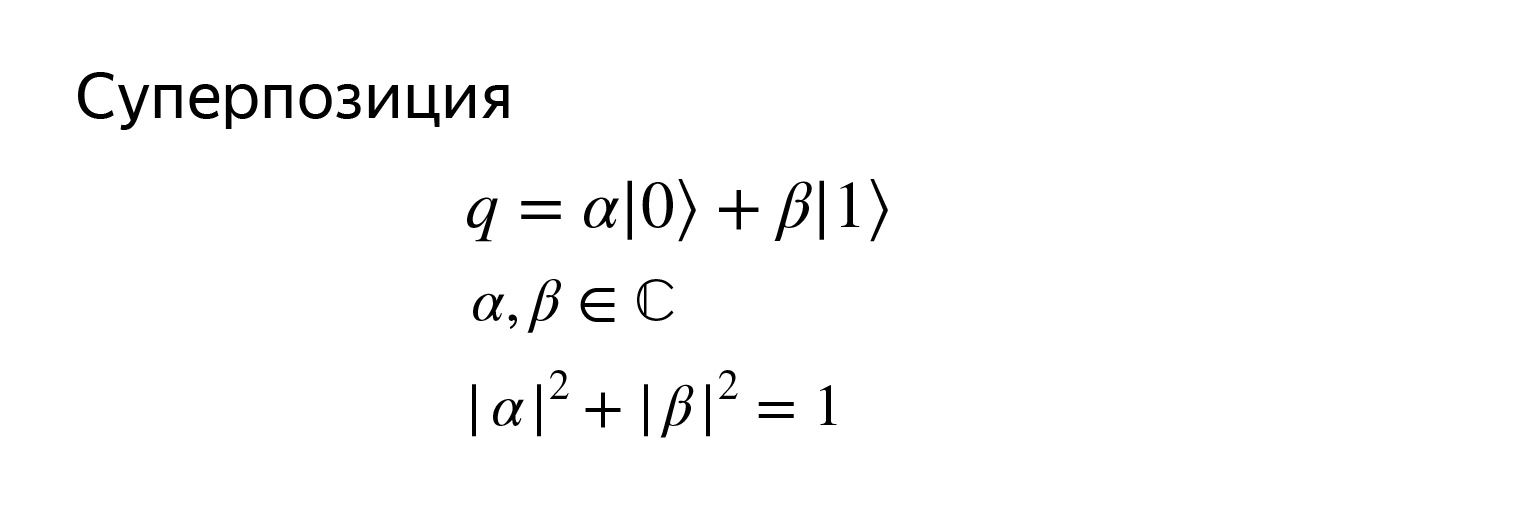
そして、ベクトルなので、その状態はこのように書くことができます。キュービットqは、2つの基底ベクトルの重ね合わせです。αとβは複素数ですが、絶対数ではありませんが、その2乗の係数の合計は1になります。
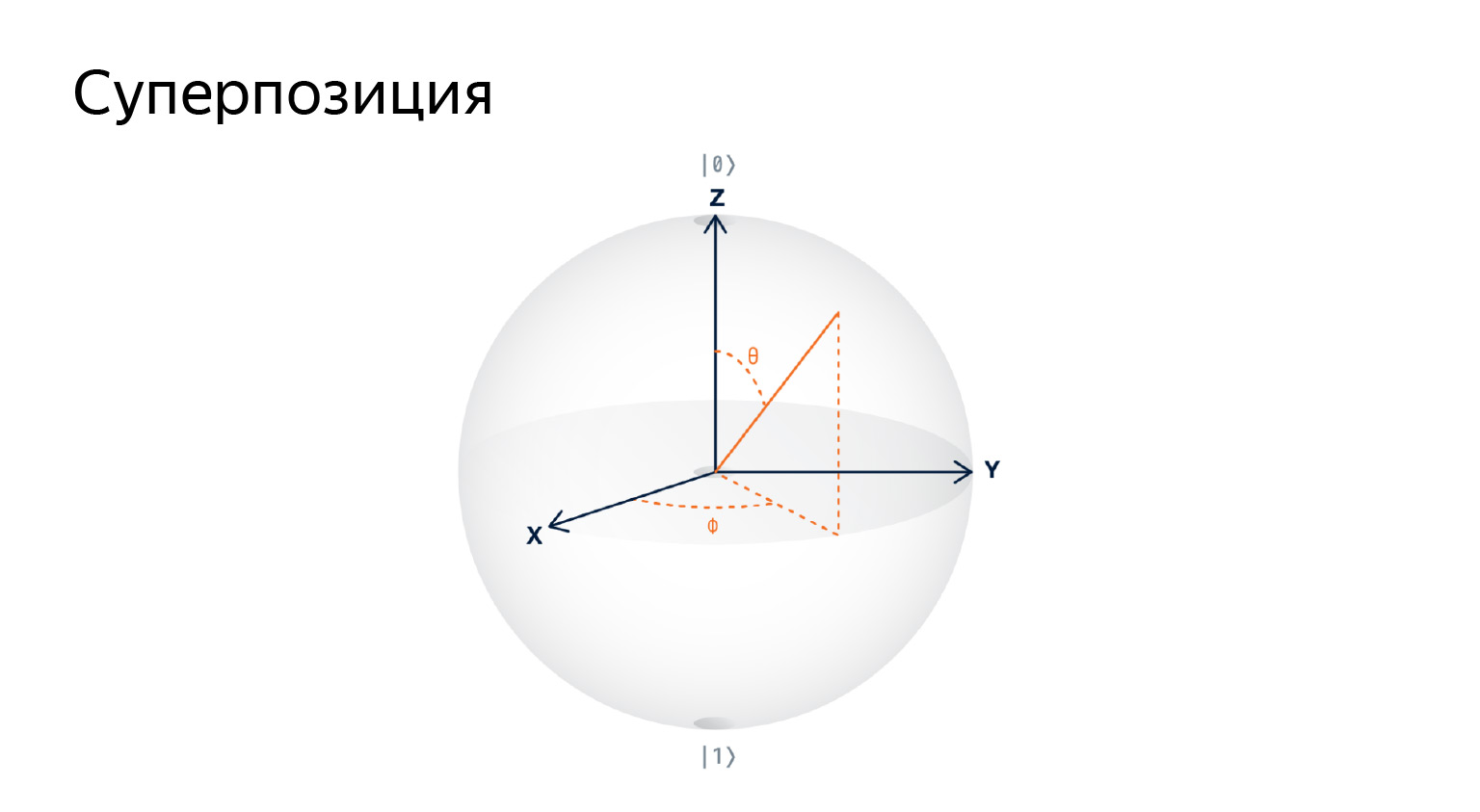
これを描こうとすると、キュービットは3次元球上のベクトルであることがわかります。それは単なるベクトルであり、無限の量があるので、無限の情報を1つのキュービットに格納できます。
あなたは写真に注意を払う必要はありません、それは単に注意を引くための視覚化技術です。
キュービットについて話しました。最も重要なのは、キュービットがベクトルであることです。複素数ベクトル空間のベクトル。それで何ができますか?
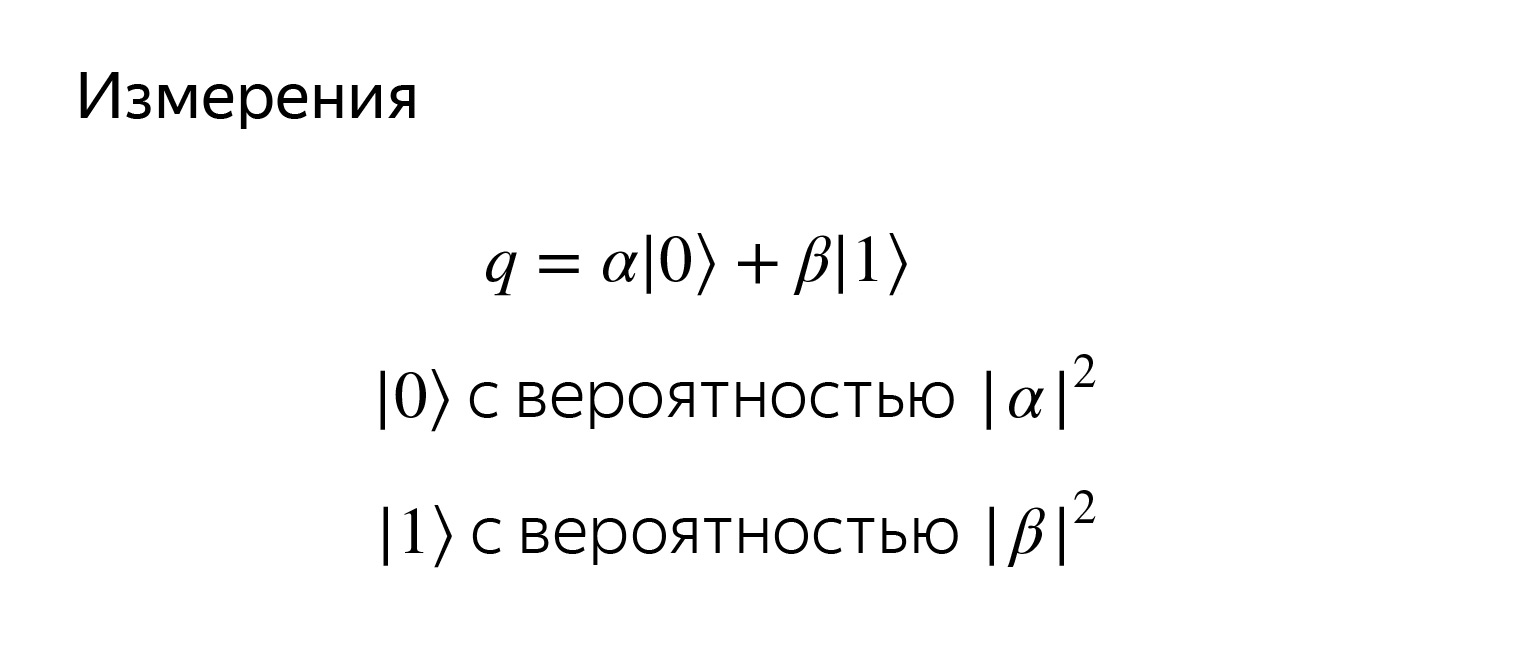
最初に使用したのは、たとえばPythonで、変数の値を計算することです。キュービットの状態を読みたいと思います。しかし、αとβの正確な意味はわかりません。
キュービットを見ようとすると、それを読んで、対応する確率を持つゼロまたは1を取得します。確率は、対応する基底ベクトルへの単純な投影です。
たとえば、キュービットのクローンを作成することもできます。これを、ある変数を別の変数に割り当てると呼びます。残念ながら、これは量子の世界ではできません。

代入演算はなく、これは先ほど言ったことと非常に関連しています。正確な値を確認することもできません。これは基本的な結果です。それは非常に簡単に証明されます:矛盾によって、文字通り2行の比較です。
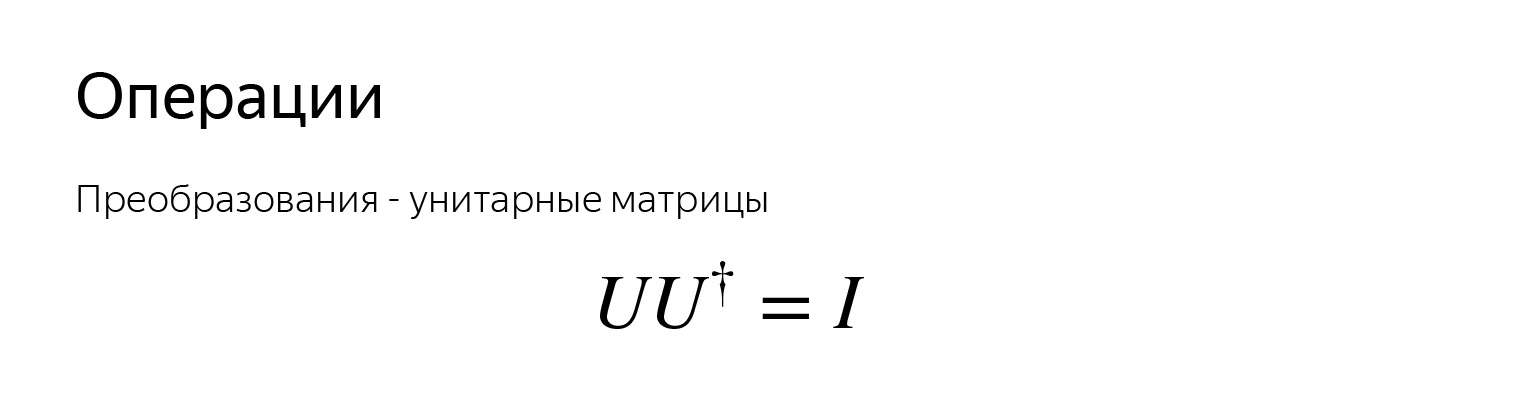
読み取ることができないキュービットがあり、クローンすることはできません。あなたは何ができますか?
キュービットはベクトルです。ベクトルを取り、球の周りを回転させることができます。回転するには、この回転を行う行列を考えることができます。キュービットのすべての演算は行列です。彼らは単一と呼ばれています。
単一性-そのような条件が満たされるために、ここでは狡猾に書かれています。このアイコンは、転置された複素共役行列を示します。このプロパティは非常に重要です。つまり、どの操作にも逆が存在します。つまり、ベクトルをどのようにねじっても、いつでも元の位置に戻すことができます。常に逆の操作があります。
どのような操作が可能か見てみましょう。古典的なケースで慣れていること。ゼロがあり、それを1に、またはその逆に変えることができます。
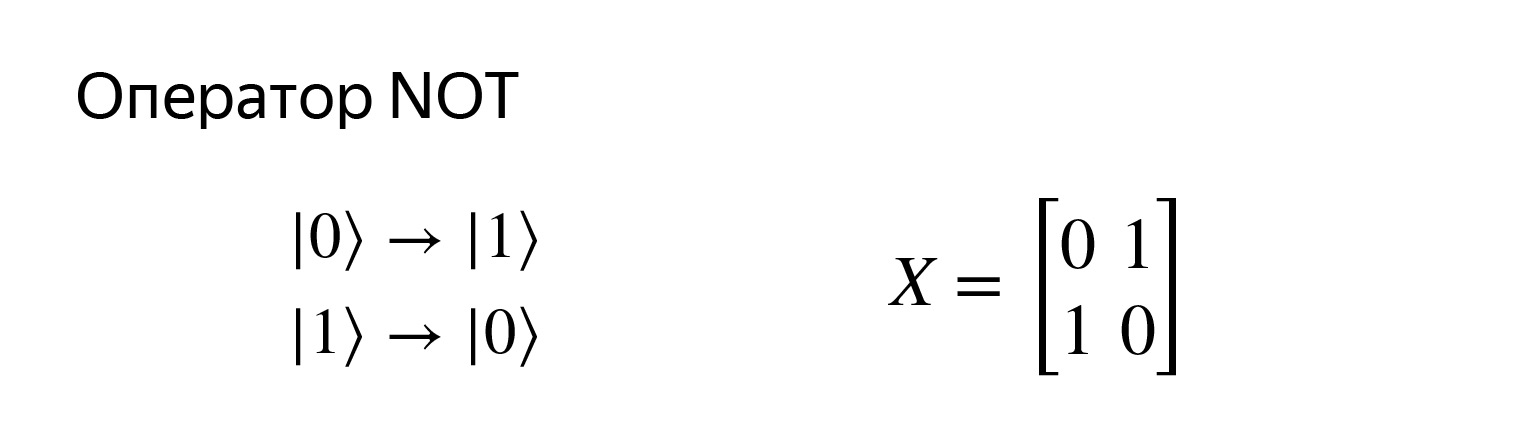
これは否定演算子であり、非常に簡単です。このようなマトリックスで記録されます。掛け算しようとすると、私たちが望むものを正確に得ることができます。
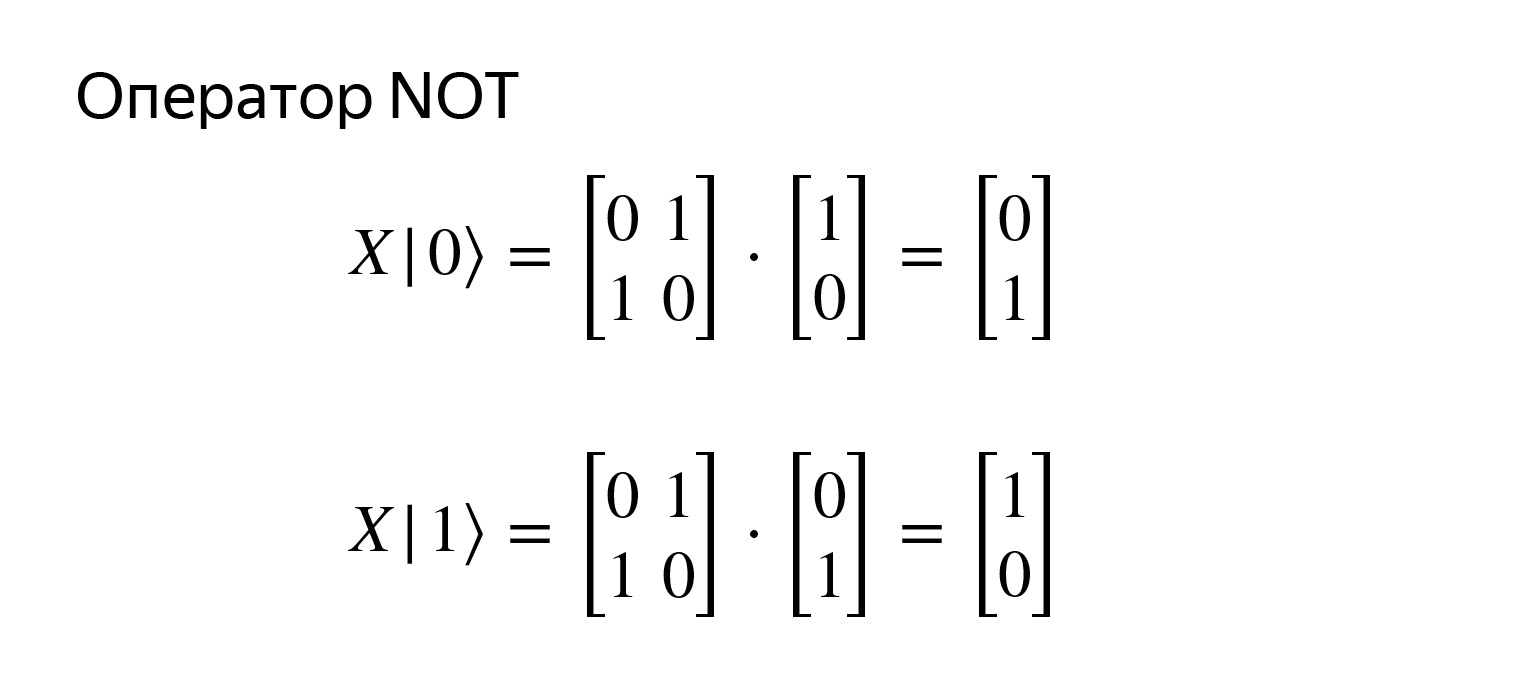
ここにも描いてもらいました。複雑なことは何もありません。否定演算子には標準の表記であるX演算子があります。考えてみると、これはいずれかの軸を中心とした回転です。そして、演算子YとZ、他の軸の周りの回転がありますが、これは現在それほど重要ではありません。
そして、量子ビットを無効にする量子コンピューターで最初のプログラムを実行することができます。
しかしもちろん、量子コンピューター科学では、Pythonで書くことはほとんどありません。スキーマをより頻繁に使用します。

図は通常、次のようになります。水平線は単にキュービット値です。ここには5つ描かれています。そしてブロック-私たちが行う操作。
最初のブロック。ここに測定装置が描かれています。これは、最初のキュービットの内容を測定したいだけであることを意味します。
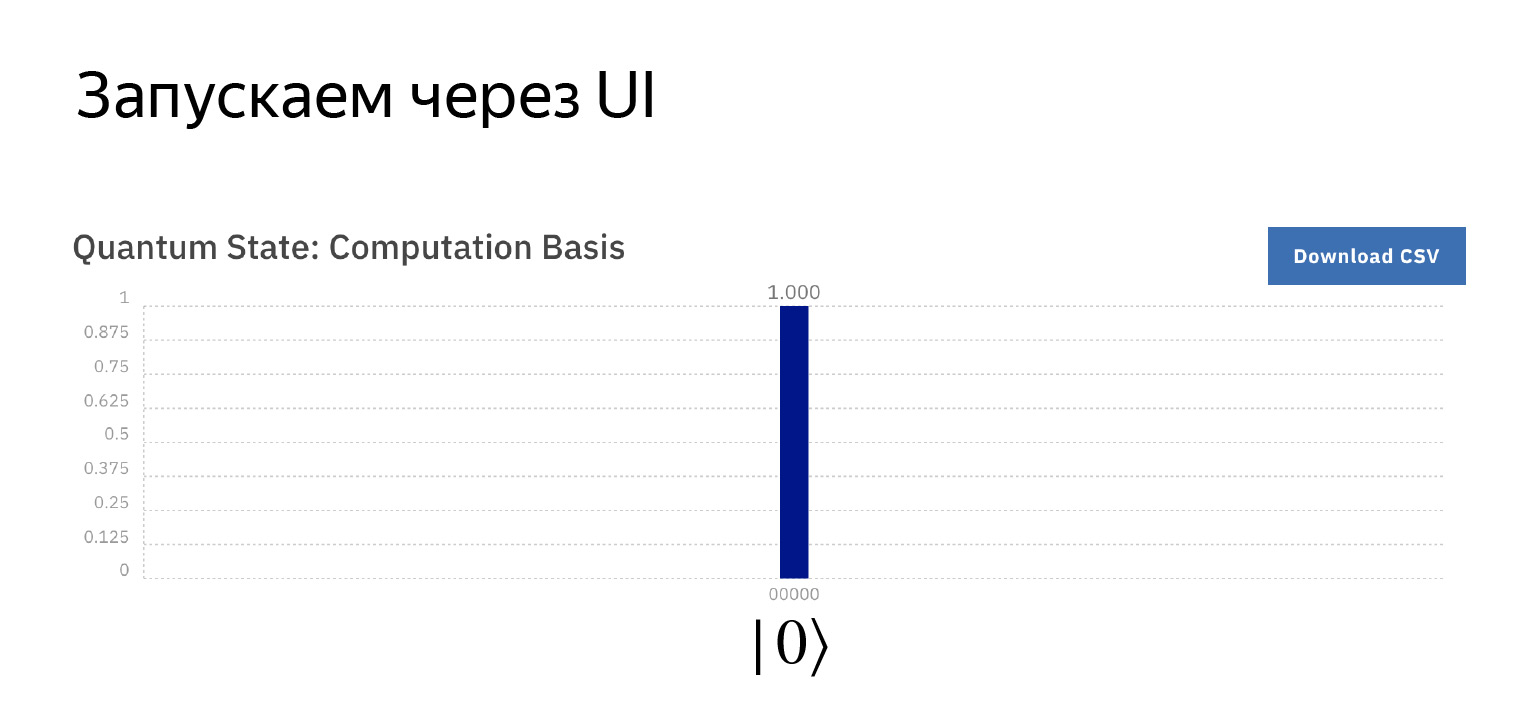
これを実行すると、1の確率でゼロが得られます。なぜなら、これらはこの状態で初期化されており、何もしなかったからです。
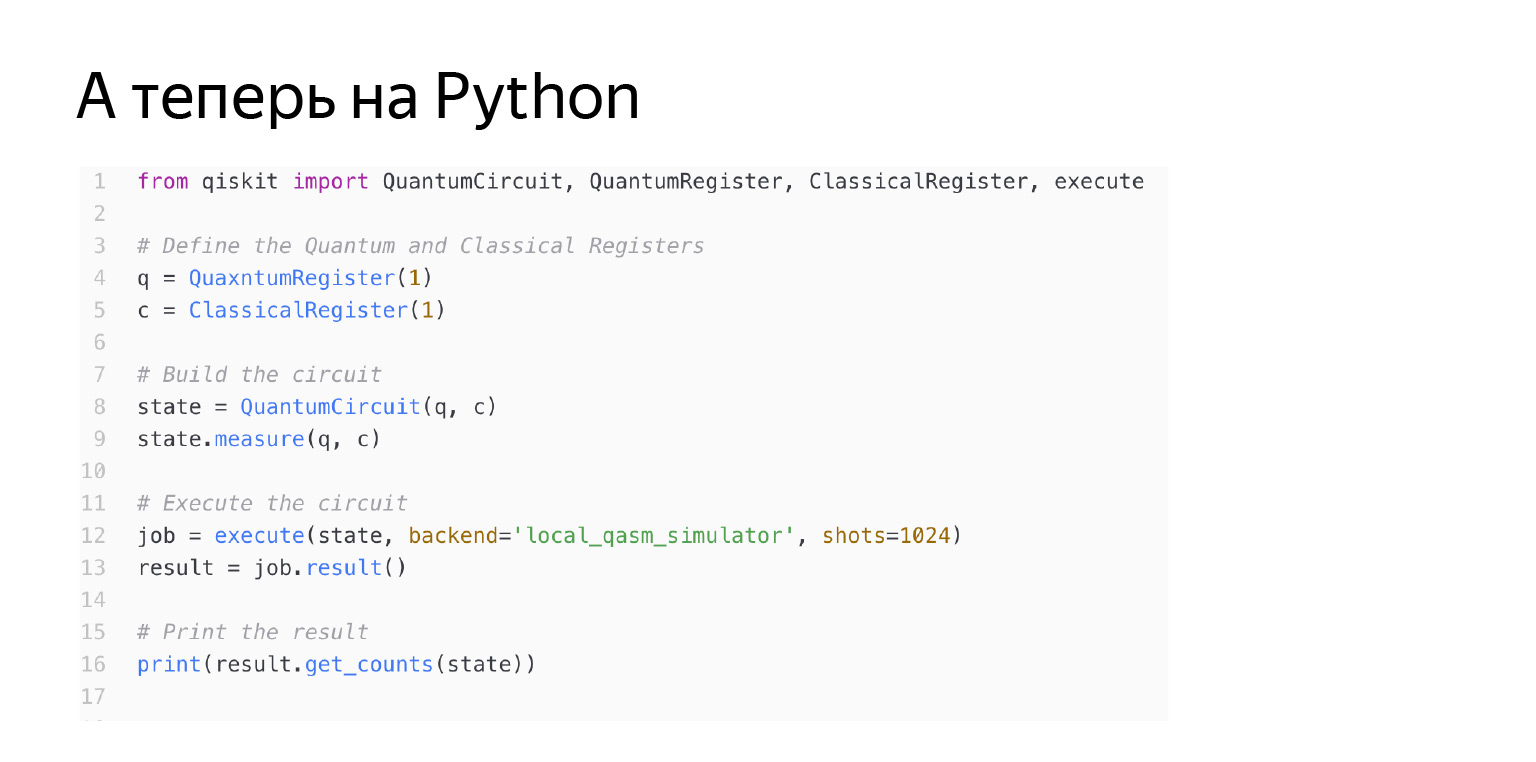
そのようなことはqiskitライブラリを使用してPythonで書くことができます。ここで行ごとに何が起こるか見てみましょう。まず、量子レジスタを起動します。ここでは1つのキュービットからオンにしています。そして、古典的なレジスタ。どこかに測定結果を書き込むには、クラシックレジスタが必要です。つまり、量子レジスタを使用して変換を行います。結果は、古典的なもの、つまりゼロまたは1です。そして、私はこの量子古典的キュービットを持つ独自の回路を作成します。私はただ言っているだけです。Cでqキュービットを測定してみましょう。これから始めましょう。すべてうまくいきます。しかし、注意深い読者にはわかるでしょう。ここでは、私のバックエンドはローカルエミュレータであると述べています。

IBM Qでも同じことができますが、ここにはもう少しコードがあります。私たちにできるだけ早く応答するデバイスを選択し、いくつかのトークンを転送することについては、あらゆる種類の麺があります。それがすべてです。しかし、トリッキーなことは何もありません。

否定演算子を使用しても同じことができます。私が言ったように、これはX演算子です。ダイアグラムではまったく同じに見えます。同じように実行してみましょう。
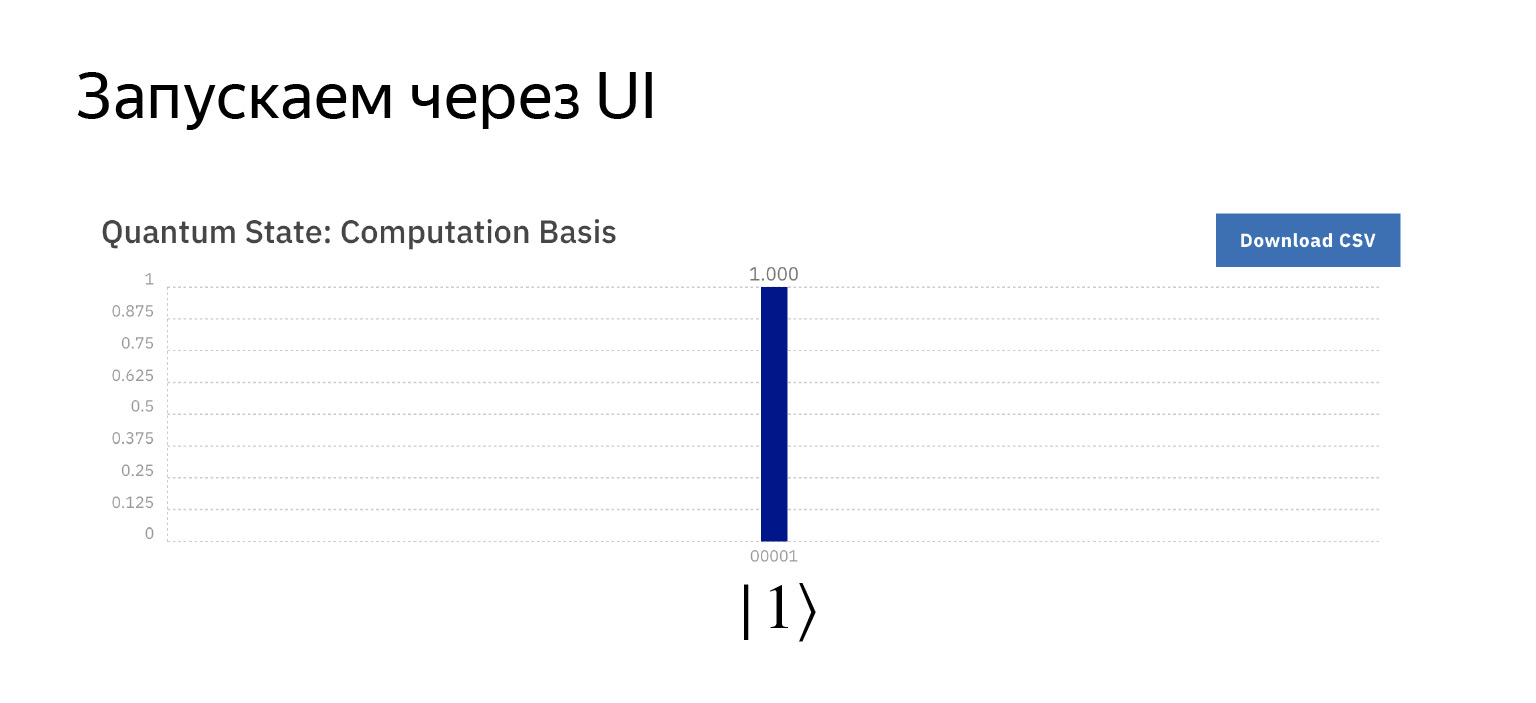
これで、1の確率で、計画どおりに1が得られます。魔法はありません。
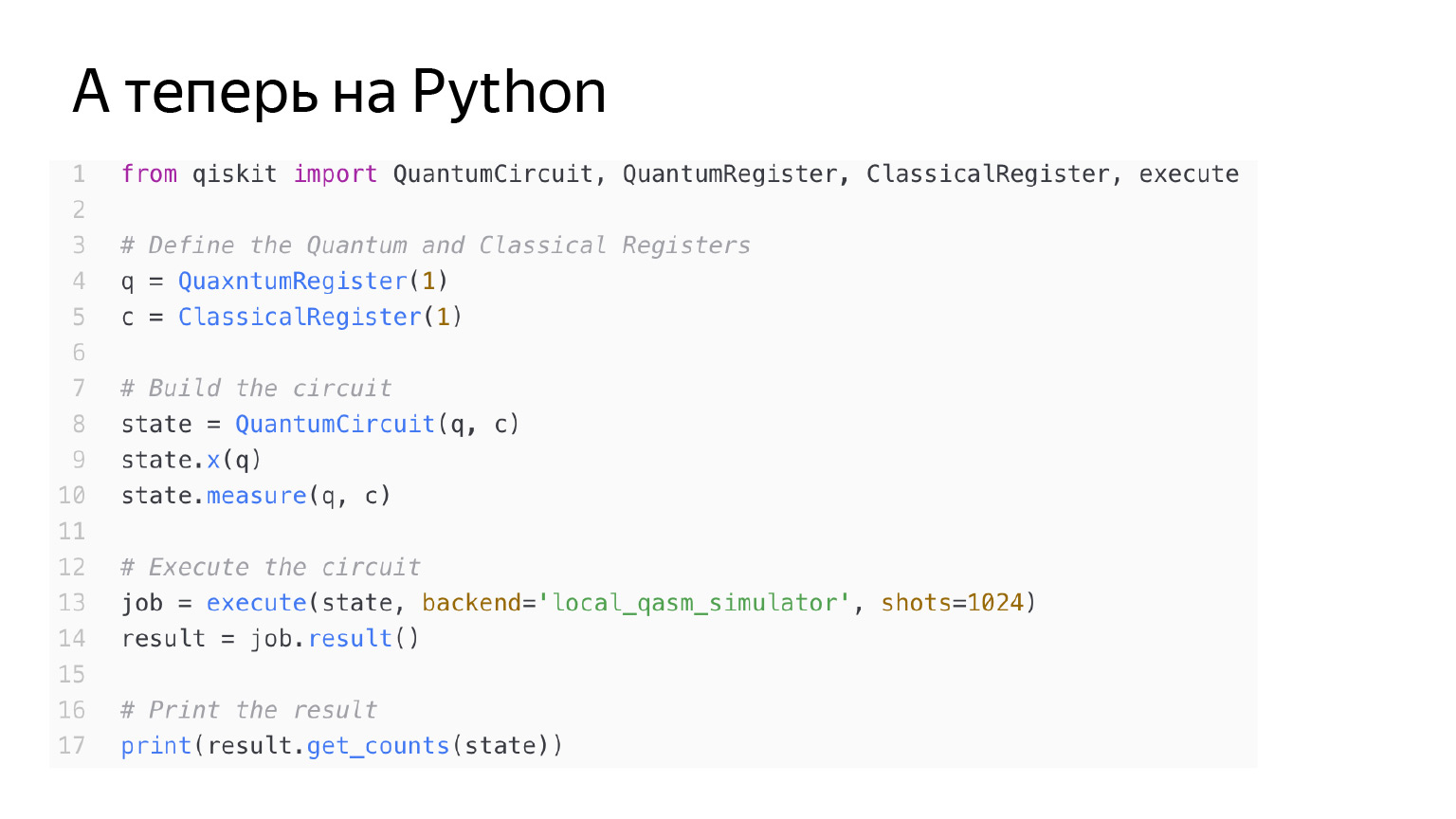
コードは同じです。ここでは、X演算子をqキュービットにも適用しています。
さて、さらに進んでみましょう。
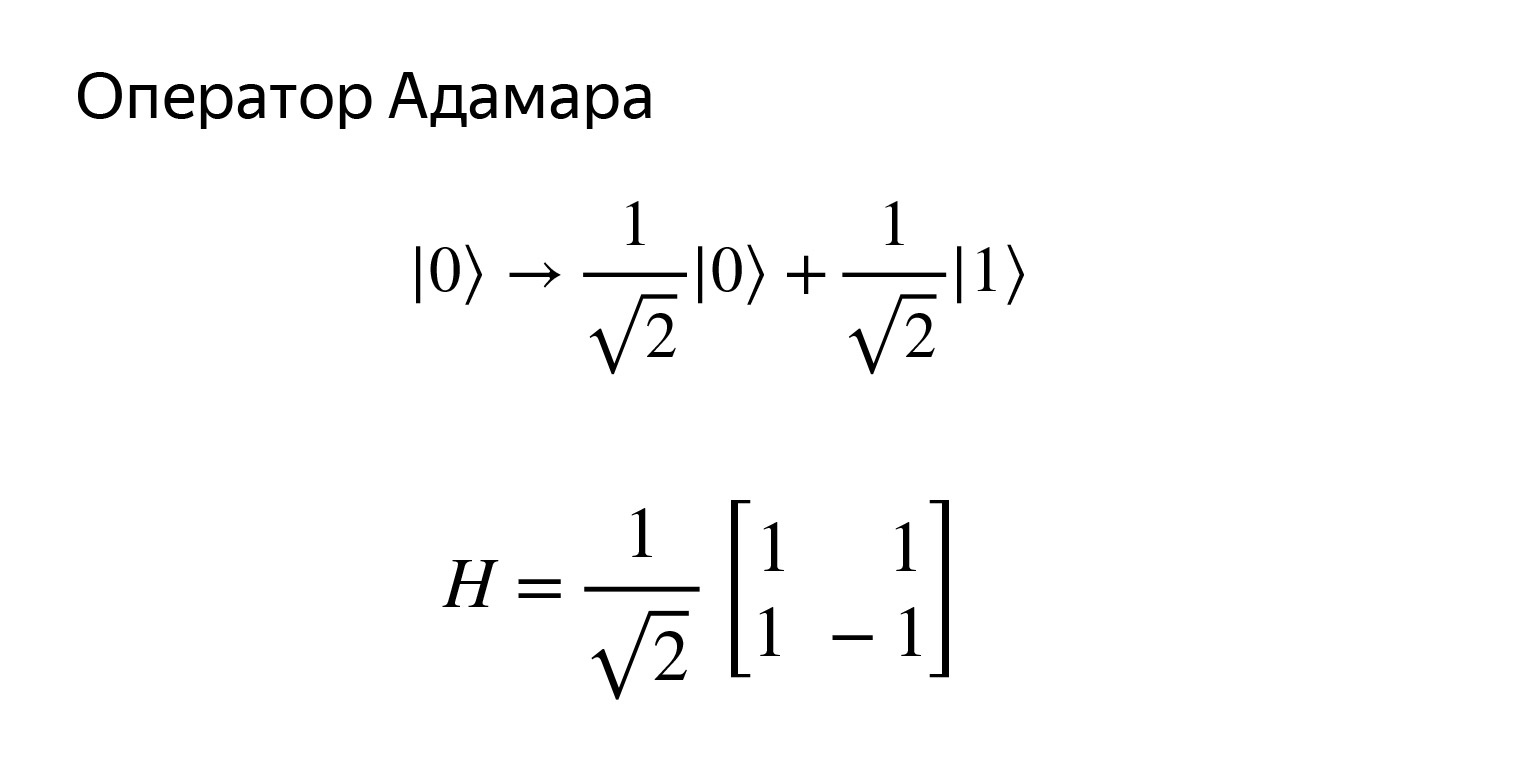
ここには非常に注意が必要なことがあります。この状態を取得してみましょう。この状態は非常に興味深いです。このような重ね合わせになります。それを測定しようとすると、1/2の確率で0または1になります。つまり、このような均一な重ね合わせとなり、何でも取得できます。
量子コイントスとは何かにたとえることができます。確率でwithと0と1を取得します。マトリックスは次のようになります。
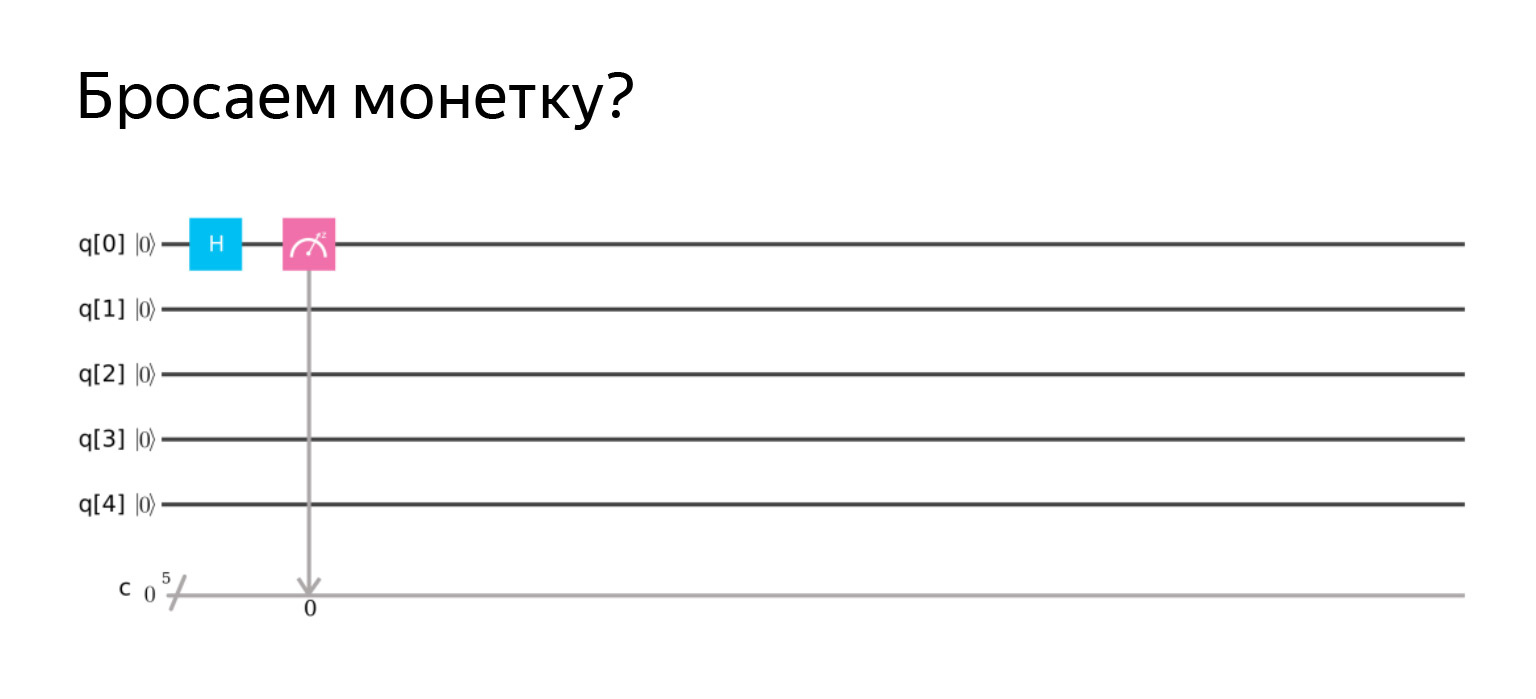
簡単に確認できますが、確認はできません。図を描いてみましょう。アダマールに敬意を表してオペレーターH。
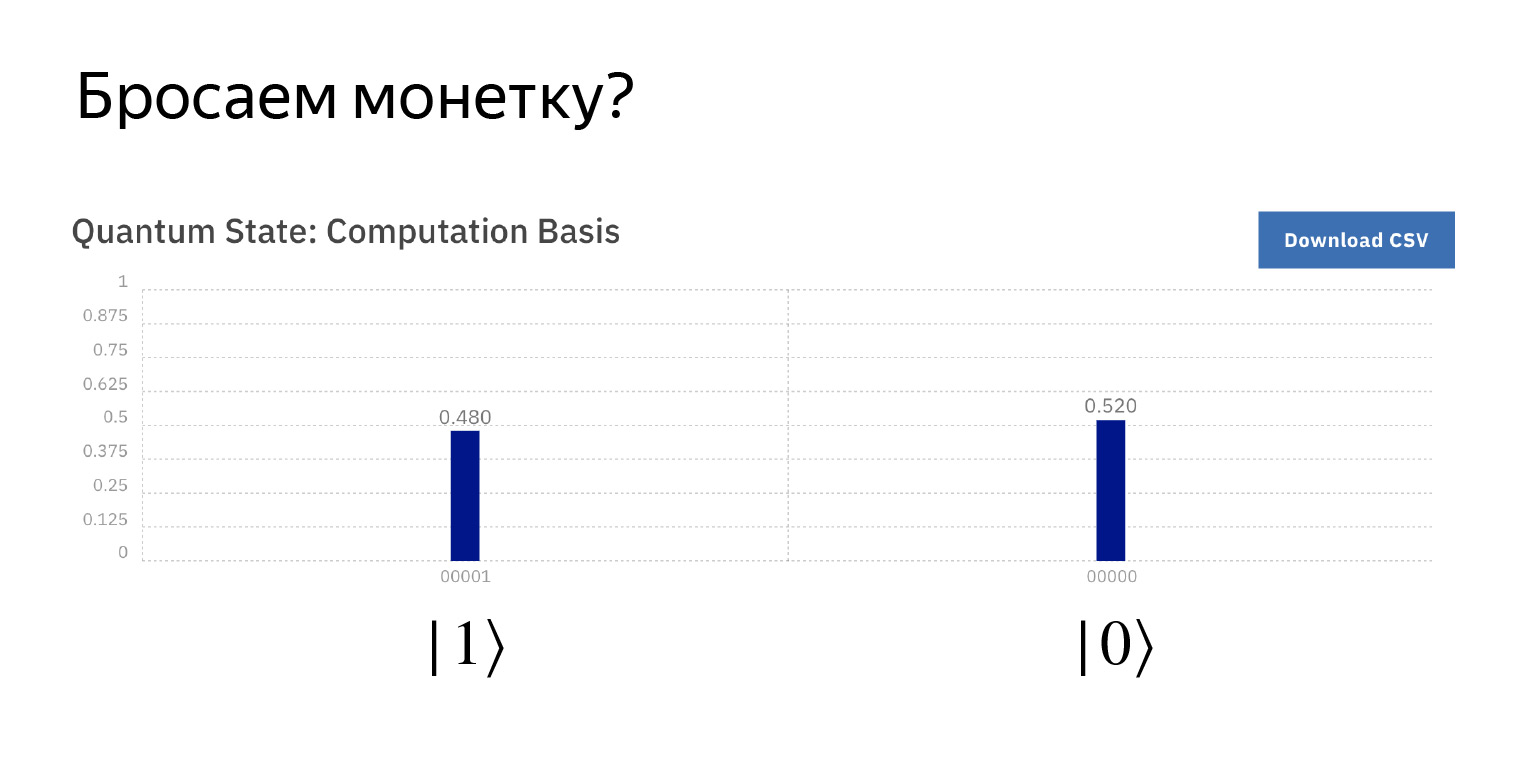
私たちが期待するものを測定し、おおよそ取得します。 ½、0、1の確率で。もう少し、少し少なくなりますが、そのように機能します。
Pythonコードは次のとおりです。Pythonの会議に参加しています。

そのような重ね合わせがあります。これにアダマール演算子を適用して測定します。
しかし、コインを2回めくることができます。これには慣れています。コインを2回めくっても何も変わりません。量子の場合にこれをやってみましょう。

アダマール演算子を2回続けて適用すると、常にゼロになります。

つまり、量子コインを2度フリップすると、アダマール演算子はそれ自体と逆であるため、常にゼロになります。自分で掛け算をすると、常に1を受け取ります。ここに事があります。
したがって、1つのキュービットで何かを実行できます。ねじったり、ねじったり、測定したりできます。さらにキュービットを追加してみましょう。クラシックの世界で何をしているのですか?単純な論理演算「or」と「and」を取り、実行します。

量子世界では、完全に可逆的ではないため、これを行うことはできません。つまり、「and」演算でゼロを取得すると、初期値が何であったかを知ることはできません。
そして、量子の世界では、私が言ったように、操作は常に可逆的なユニタリ行列です。では、どうやってプログラムするのですか?私たちが慣れていることはすべて崩れかけています。しかし、新しいヒーローが現れます。これは、いわゆる制御された否定のオペレーターです。

Pythonで記述している場合、次のようになります。最初の量子ビットが1の場合、2番目の量子ビットを反転させましょう。これは行列ではなく、これは演算子がどのように見えるかです。しかし、原則として、私が言ったことはここに書かれています。最初のキュビットに単一性がある場合、2番目は反転されます。
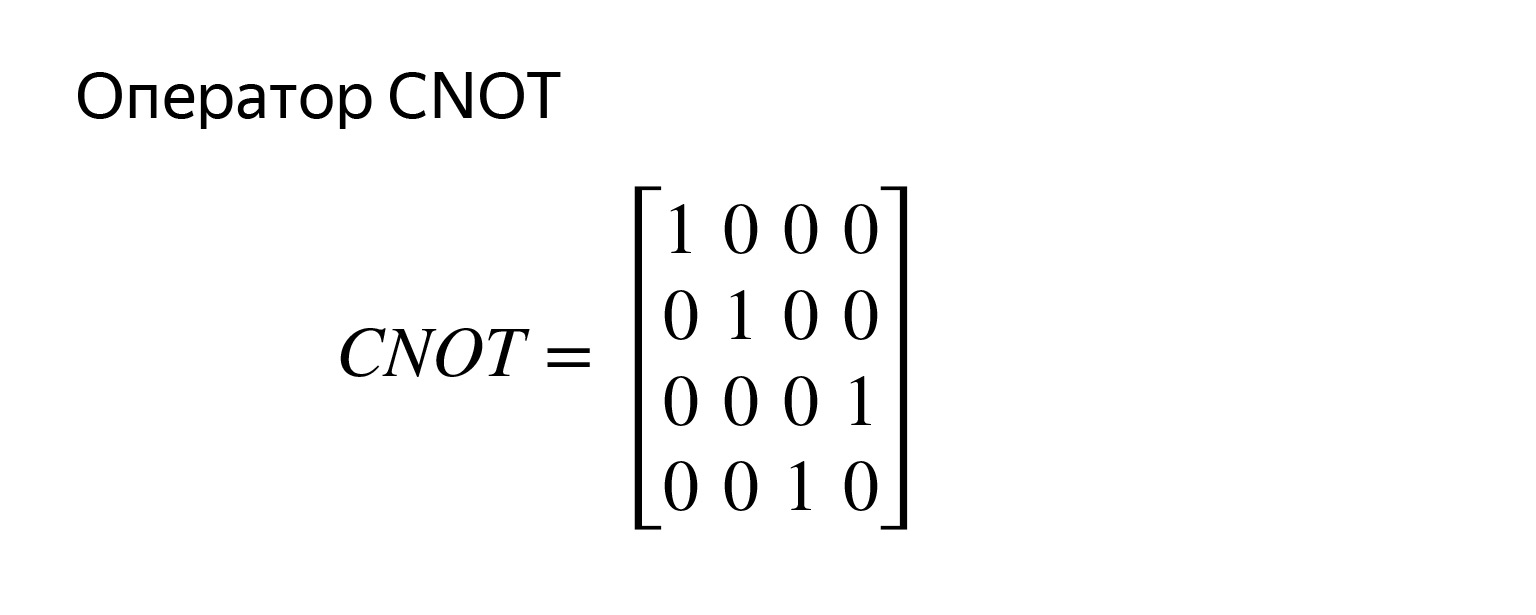
マトリックスはすでに4 x 4です。 2つのキュービットの場合、次のようになります。アスタリスクを乗算して問題を残し、これが正しいかどうかを確認します。

このことはプログラムすることもできます。ロケット科学はありません。必要なのは、2つの量子ビットと2つの古典ビットを持つ回路を作成し、CNOTだけでなく、CXによって否定を制御するだけです。
否定はX演算子だったので、原則としてすべてが論理的です。そして、あなたは図を描くことができます。スキームは次のとおりです。
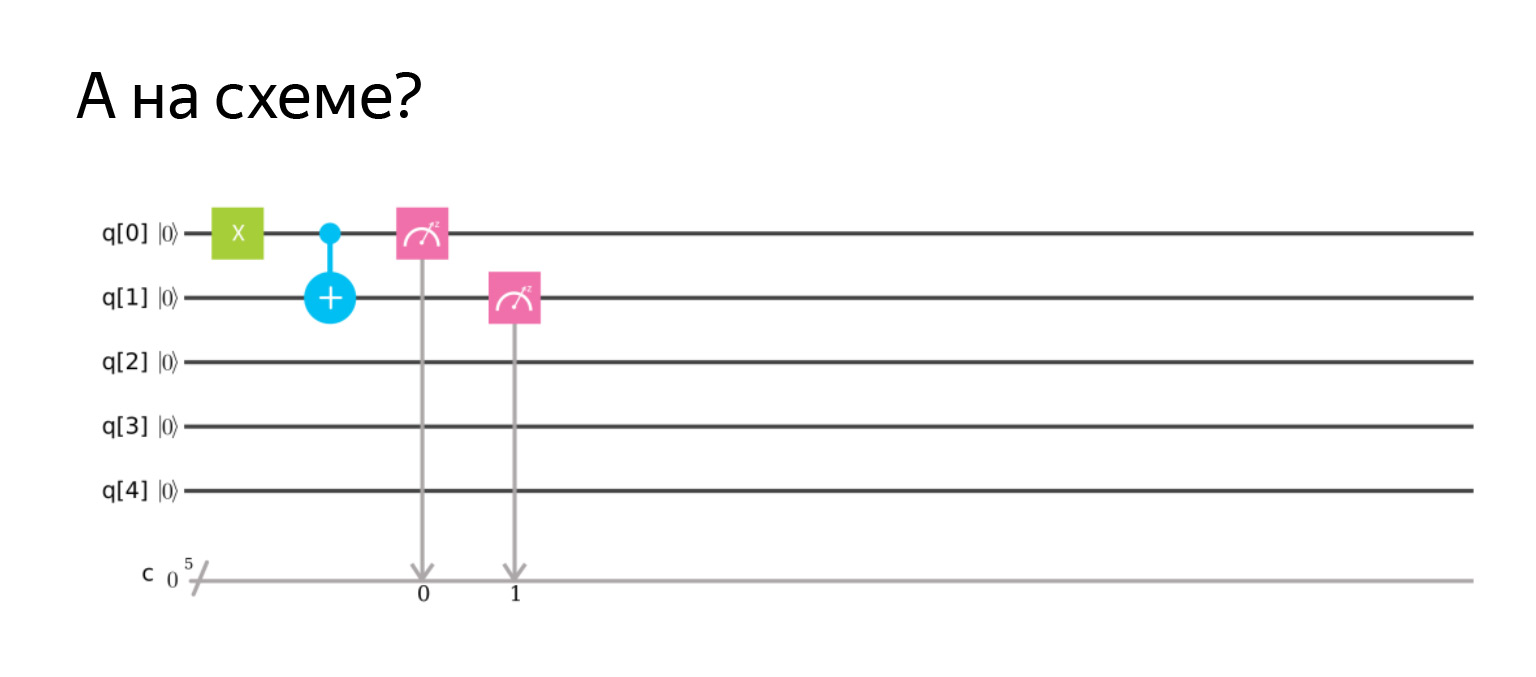
つまり、制御された否定は、変更したいキュービットのプラスです。そしてポイントは、コントロールです。ここで、量子ビットが1の場合、2番目のものを変更します。

ここでは具体的に最初に最初の値を反転して1にしてから、両方を測定して結果を取得しています|11⟩。すべてが期待通りです。
しかし、今こそすべての知識を一緒に使う時です。

私たちが知っている3つまたは4つの演算子すべてを1つのスキームに固執しましょう。つまり、アダマール演算子を最初の演算子に適用します。 2つ目を反転させてから、すべて一緒に、制御された否定と測定を行います。
まだ実行していませんが、何が起こるかを推測してみましょう。
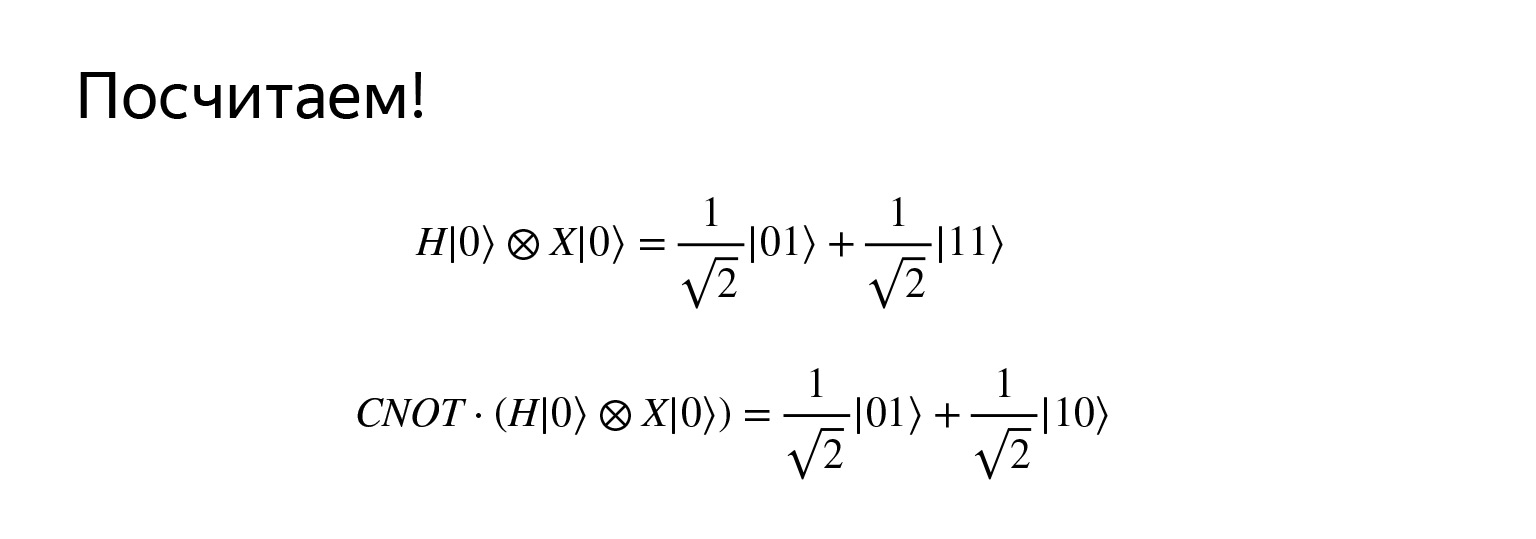
最初の量子ビットにアダマール演算子を適用し、2番目の量子ビットを否定すると、そのような重ね合わせが得られます。チェックに時間をかけたくないので、簡単に乗算できます。しかし、立場は非常に興味深いです。第一に、これはユニフォームに非常に似ています。第二に、制御された否定も取る場合、この状態はエンタングルドと呼ばれます。

状態は混乱しています。なぜ?測定してみましょう。最初のキュビットを測定し、それを状態0にした場合、2番目のキュビットは必ず状態1にあると言えます。
つまり、キュービットでこのような変換を行うと、1つのキュービットを友人に渡し、彼はニューヨークに飛んで、2番目のキュービットを自分で測定します。彼のキュービットの状態が正確にわかります。これは、量子もつれまたは量子結合の効果と呼ばれます。そして、これが量子計算が機能する主要なメカニズムです。変化し、それらは非常に強固に接続され、測定中は| 00 weまたは|11⟩しか得られません。
この機会に、私の考え

気が散ったのは、彼がいつも違う靴下を履いていたことです。そして、彼の同僚は彼について冗談を言った:彼が片足で部屋に入って、靴下がピンク色であるのを見るならば、我々は2番目の靴下がピンク色でないと確かに言うことができる。だからそうなるのです。
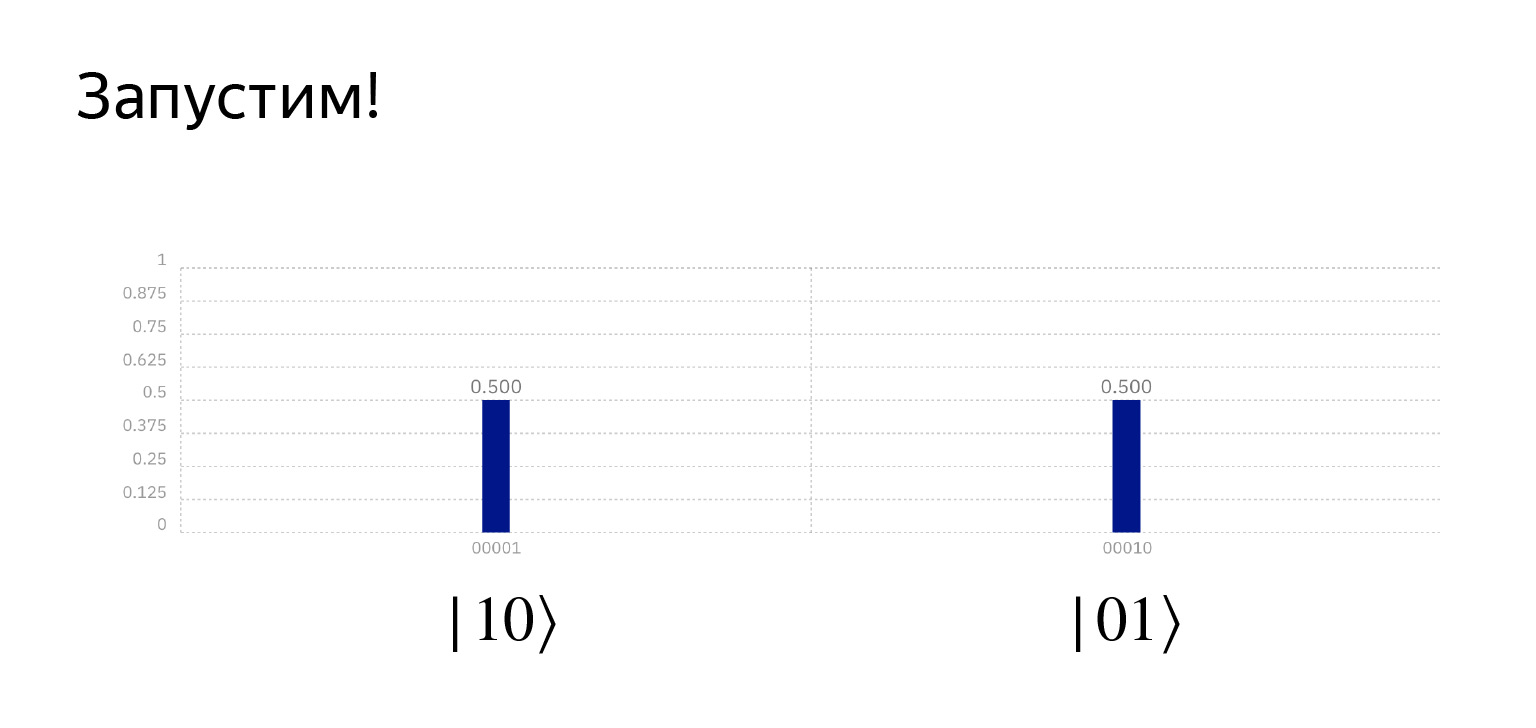
これを実行すると、必要なものが正確に得られます。ここはすでにかなり面白いです。確率はちょうど0.5ですが、これは偶然です。
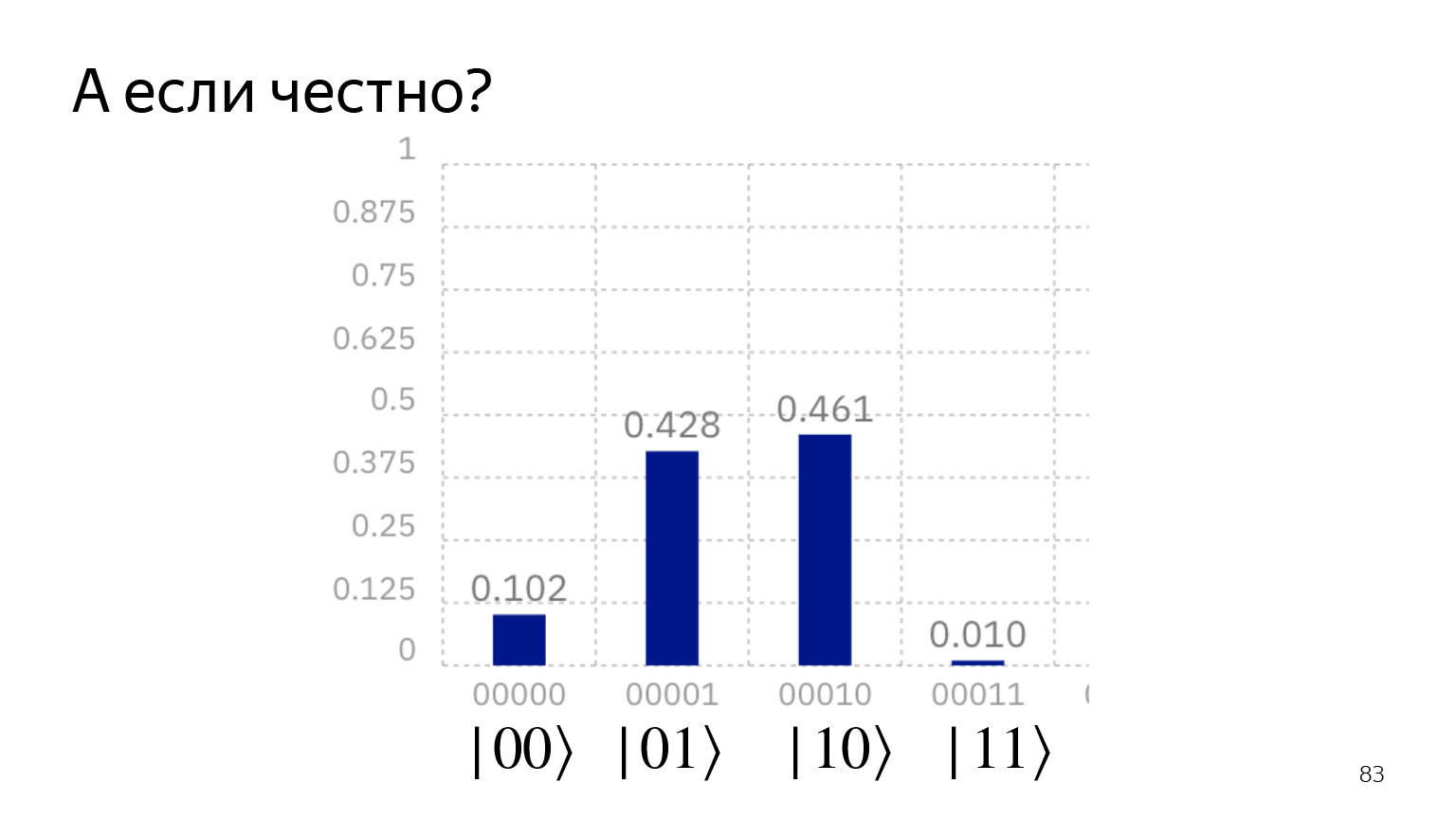
量子コンピュータで正直に実行すると、この画像が得られます。状態|00⟩は取得できず、状態|11⟩は取得できません。しかし、それでも機能します。現在のテクノロジーの状態では、常に簡単に抑制できないノイズが存在します。そして彼らはこれに苦しんでいます。
しかし、古典的なコンピュータサイエンスを覚えているなら、それは同じことです。エラー修正コードなどです。キュービットが小さすぎてエラー訂正に余分なビットを費やすことができないだけです。
今、私が約束したように、アルゴリズムのいくつかの例。しかし、これらはアルゴリズムの分析のない根拠のない例にすぎないので、見て、考えて、興味を持つようになります。

最初のアルゴリズムは、冒頭で説明したDeutschに関連しています。これはDeutsch-Jozyアルゴリズムです。そして、彼は次のことを行います。 n個の変数にブール関数があるとします。そして、それが一定であるか、またはバランスが取れていることは確かです。バランスが取れているとは、引数のちょうど半分がゼロになり、残りの半分が1になることを意味します。それが定数であるかどうかを古典的にチェックしてみましょう。
これを行うには、すべての可能なオプションの少なくとも半分をチェックする必要があります:2 n – 1 +1オプション。量子アルゴリズムでは、関数自体のn回の計算で、関数自体へのn回の呼び出しでこれを行うことができます。これは、指数的に低いヒット数です。
2番目の例は、おそらく量子コンピューターがすべての暗号を解くと言われているため、だれにでもよく知られています。量子を非常にすばやく因数分解できます。

難易度の見積もりがここに示され、素晴らしい例があります。 2011年には、数値15は実際のコンピューターで計算され、7キュビットを要しました。

しかし、すべてがそれほど悪いわけではありません。量子コンピューターがRSAを破ることができるレベルに達した場合、量子化後の暗号化はすでに存在しています。エラーのある学習に基づいています。これは、小さなエラーが問題に導入されたため、答えを見つけるのが非常に困難な場合です。通常、これらはある種の方程式または連立方程式です。これがアルゴリズムの例です。読みたい人は誰でももっと詳しく読むことができます。
最も興味深い:New Hopeアルゴリズムは、これに基づいており、すべての人類の新しい希望です。 2016年、Chrome はこのアルゴリズムのサポートを追加しました。ここにブログへのリンクがあります。これは私の考えではありませんでした、すべてが本当にです。未来はすでにここにあります。
最後にいくつかのリンクがあります:
- , : Michael A.Nielsen and Isaac L. Chuang, «Quantum Computation and Quantum Information». , . .
- IBM Q: quantumexperience.ng.bluemix.net
- IBM Q User Guide: quantumexperience.ng.bluemix.net/proxy/tutorial/full-user-guide/introduction.html
- Qiskit: qiskit.org
- :
nplus1.ru/material/2017/06/07/quantumcomputers
nplus1.ru/news/2017/05/26/quantum-blockchain
これは多かれ少なかれすべてです。それを付け加えたいのは、約50年前、ドイツが量子情報科学を始めたとき、コンピューターは大規模でした。それらはいくつかの会社によって作られました。彼らはワードローブほどの大きさでした。そして今、大体同じ会社が大きな量子コンピューターを作っています。そしてもちろん、50年後に何が起こるかはわかりません。
お気に入りの検索エンジンを入力しようとすると、今日、量子プログラマーの求人を見つけることができます。もちろん、もっと多くの研究がありますが、それでもなおです。感謝。