社会的距離の数学は幾何学のレッスンです

人々を1メートル半離して安全にオフィス、学校、その他の公共の場所を再開する方法の課題は、数学者が何世紀にもわたって研究してきた問題に帰着します。

球 のパッキングのようなトピックは数学者だけにアピールするように思われるかもしれません。平面上に円を配置したり、空間内の球を配置したりするための最も効果的な方法を探すことに興味がある人は他に誰ですか？



しかし、今日、世界中の何百万もの人々がまさにこの課題について考えています。



社会的な距離を保ちながら建物や公共スペースを安全に開く方法を決定することは、特に幾何学の練習です。各人が他の人から少なくとも1.5メートル離れている必要がある場合、教室またはダイニングルームに座ることができる人の数を計算するには、フロアプランに重複しない円を詰める必要があります。







当然、コロナウイルスと戦うためには、この幾何学的な問題よりも多くの問題を解決する必要があります。ただし、これには、化学における結晶構造のモデリングや情報理論における抽象的なメッセージ空間のモデリングと同様に、円と球のパッキングが役割を果たします。この作業は、一見簡単そうに見えますが、歴史上最も偉大な数学者の心を占領しており、この分野で最も興味深い研究は、今日、特に高次元で行われています。たとえば、数学者は最近、8次元および24次元の空間にパックするための最良の方法を見つけました。これは、携帯電話とスペースプローブとの通信の両方で使用されるエラー修正コードを最適化するために必要な手法です。それでは、スペースを最も単純なフォームで埋めようとしたときに発生する予期しない複雑さのいくつかを見てみましょう。



職場でオレンジを箱に詰める場合でも、社会的に離れた場所にいる生徒を安全に座らせる場合でも、コンテナのサイズと形状はタスクにとって重要です。ただし、ほとんどの数学者にとって、球体パッキング理論は空間全体を埋めることです。 2次元では、これは同じサイズのばらばらの円で平面を覆うことを意味します。



これは、平面上に円をパッキングする一例です。ソーダパッケージの上面図のように見えます。







平面で舗装されたタイルのように、このパターンがすべての方向でどのように繰り返されるかを想像できます。円の間の小さなギャップは、平面が完全に満たされていないことを示しますが、円をパッキングする場合、これは予想されるはずです。飛行機の何パーセントがカバーされているかに関心があります。これが特定の方法の「パッキング密度」になります。



上記の方法はスクエアパッキングと呼ばれ、正当な理由で、円の中心は正方形の頂点として表すことができます。







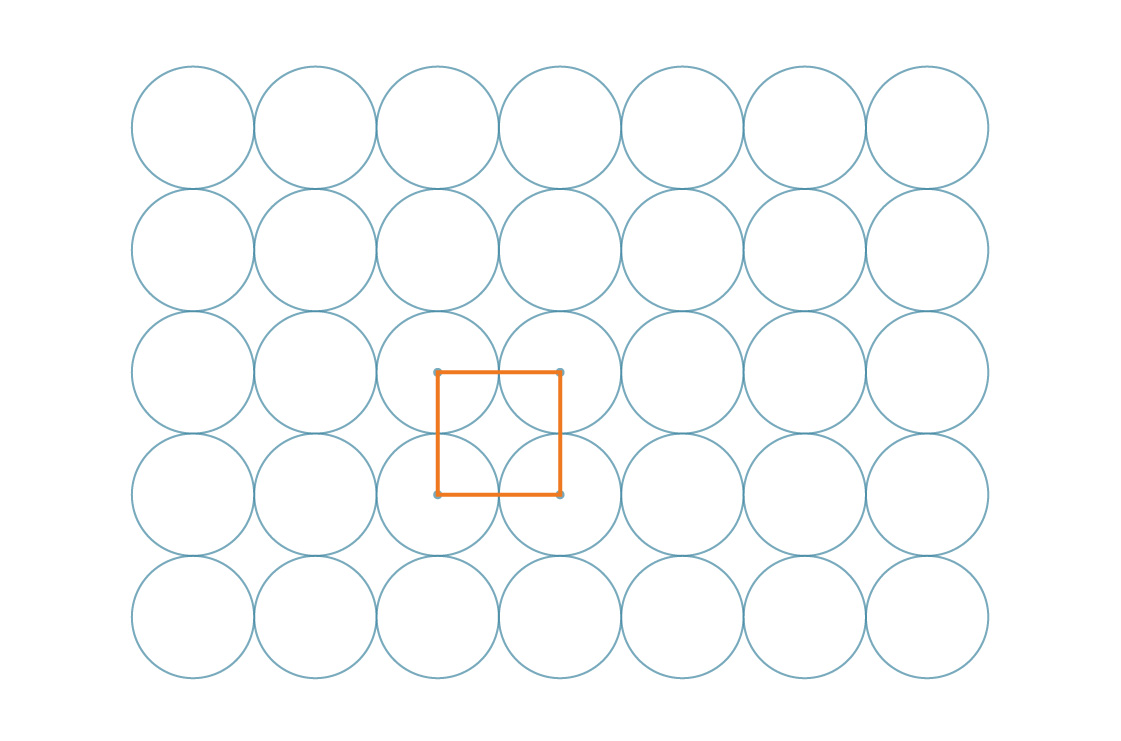
そして実際、これらの正方形自体が平面をタイル状に並べています。







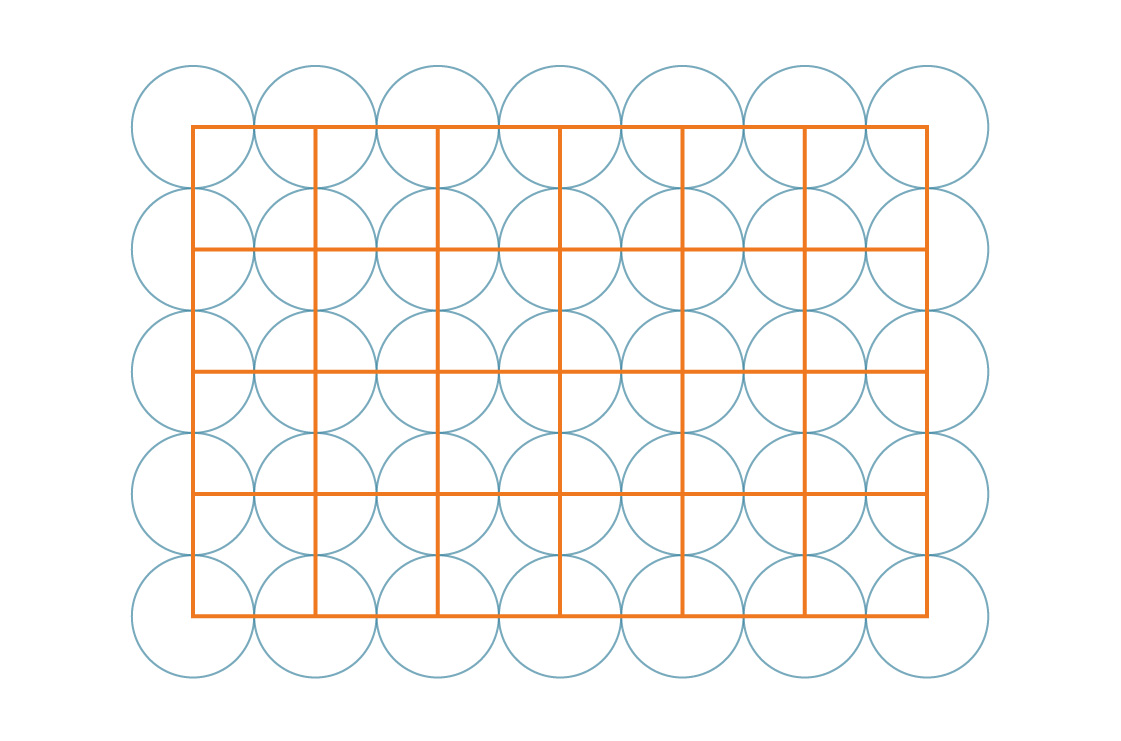
私たちのタスクは、パターンの対称性によって容易になります。これらの正方形は周期的に平面全体をカバーしているため、円で覆われている平面の割合は、円で覆われている正方形の割合と同じです。これらの正方形の1つを見てみましょう。







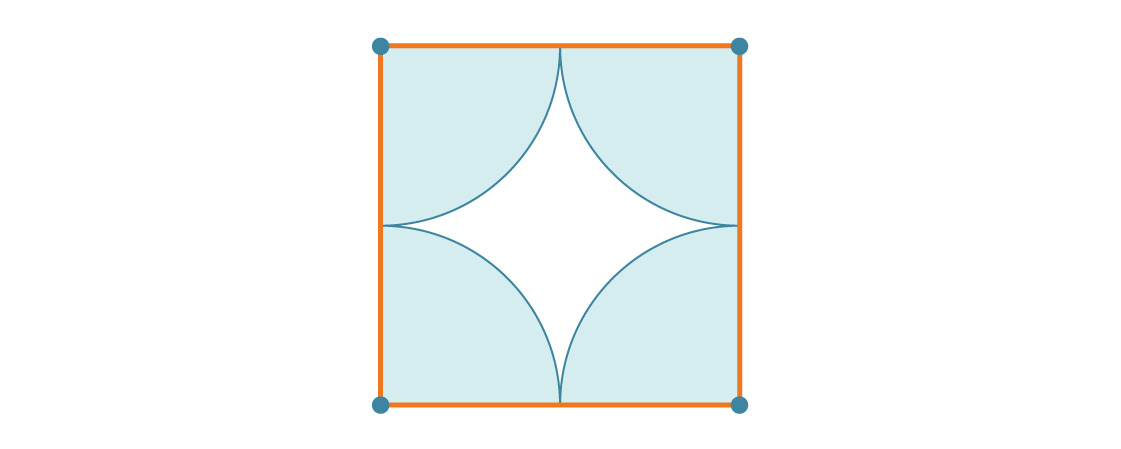
円の半径がrだとしましょう。これは、正方形の一辺の長さが2rであることを意味します。正方形の各頂点には4分の1の円があるため、各正方形のカバレッジの割合は、1つの完全な円の面積と1つの完全な正方形の面積の比率に単純に等しくなります：

$$

$$\frac{\pi r^2}{(2r)^2} = \frac{\pi r^2}{4r^2} = \frac{\pi }{4} \approx 0,7854$$

各正方形は約78.54％が円で覆われているため、平面のタイリングを考慮すると、すべて約78.54％が円で覆われています。これは、正方形のパッキングの密度です。半径rが答えから消えたことに注意してください。そして、これは理にかなっています。円のサイズに関係なく、正方形には4分の4の円があります。



このようにソーダ缶を折りたたんで隙間を埋めよ







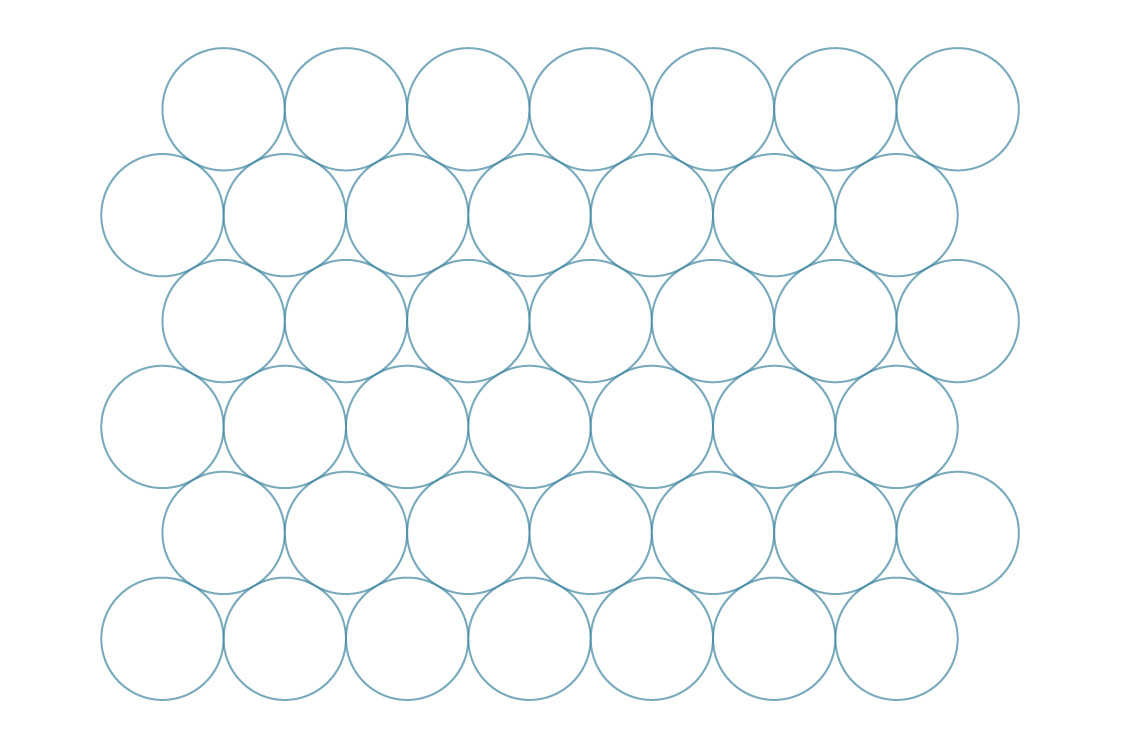
うとすると、円を平面に詰める別の方法があることがわかります。前の方法と同様のアプローチを使用して、この場合の円の中心が通常の六角形を形成すると想像してください。 ..。







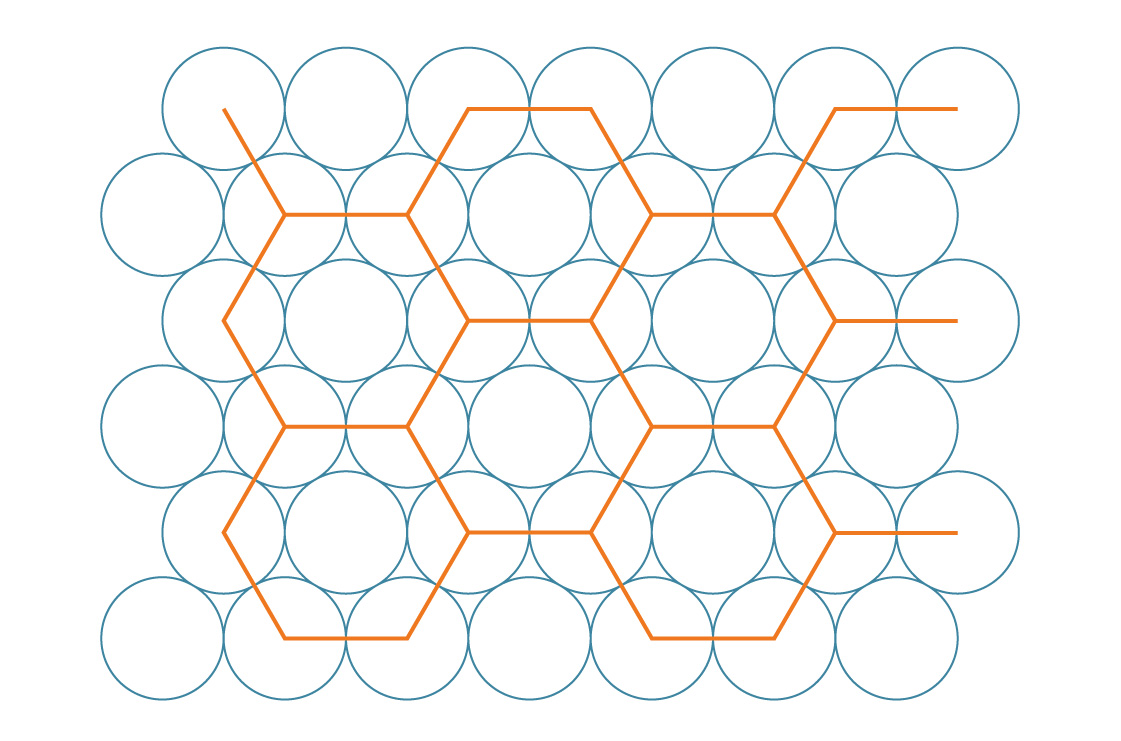
これを六角形のパッキングと呼びます。この方法は、正方形よりも効率的にギャップを埋めるようです。これを確認するために、それらのパッキング密度を比較してみましょう。正方形のような六角形は平面を完全に並べて表示するため、単一の六角形を分析することでこの方法の密度を決定できます。







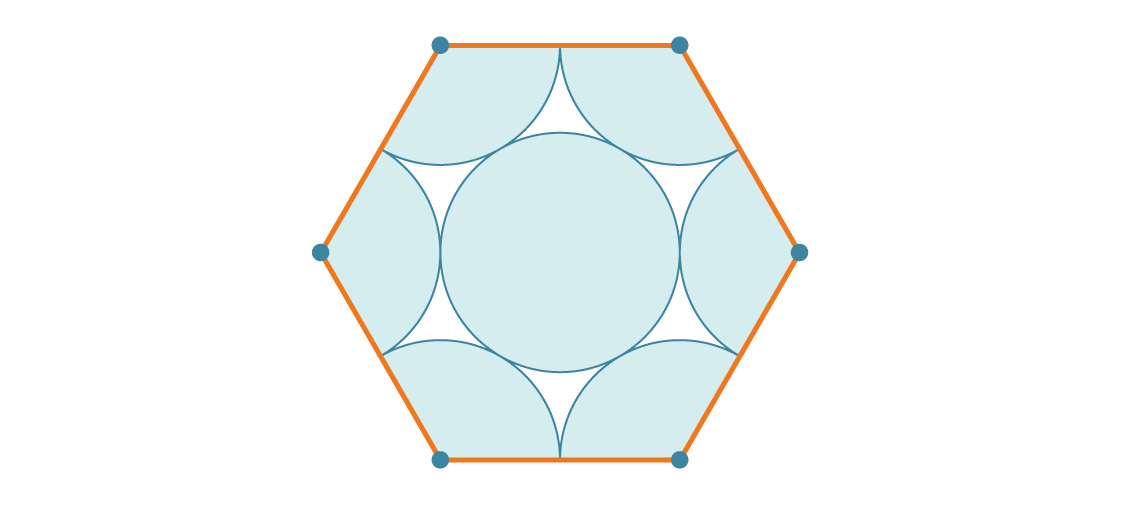
六角形のどの部分が円で覆われていますか？通常の六角形の内角は120°であるため、各コーナーに3分の1の円があります。それは2つの完全な円になり、真ん中の円は3番目になります。したがって、各六角形は3つの円で覆われています。各円の半径がrの場合、面積は3πr²です。







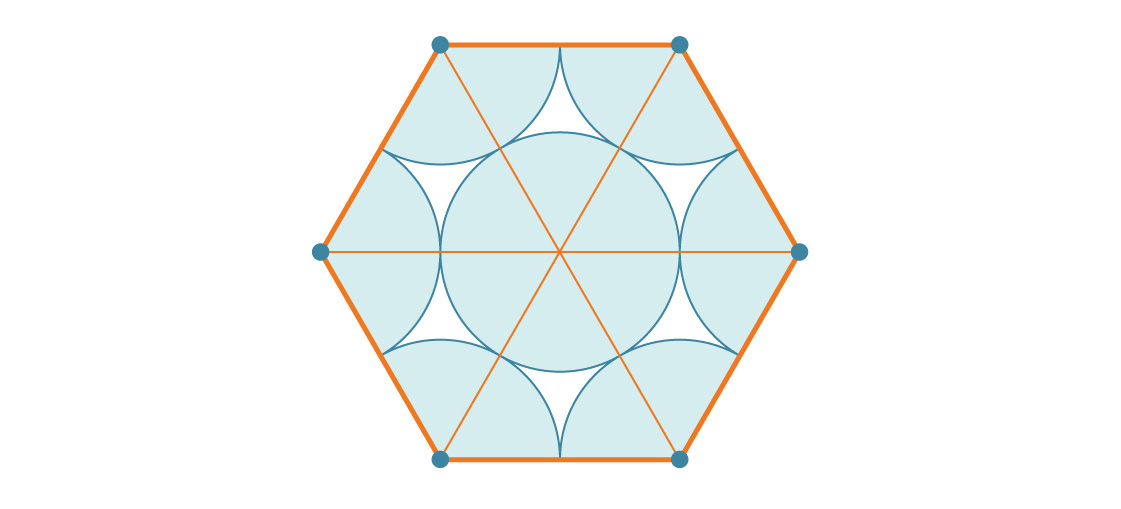
これは六角形の面積とどのように比較されますか？辺の長さsの六角形がSであり、それぞれが側長Sを有する6つの正三角形である² √3/ 4。したがって、六角形の面積は6 * sで² √3/ 4 = 6 S ² √3/ 4。六角形の辺の長さは2rなので、その面積は次のようになります。

$$

$$\frac{6 s^2 \sqrt3}{4} = \frac{6 (2r)^2 \sqrt3}{4} = \frac{24 r^2 \sqrt3}{4} = 6 r^2 \sqrt3$$

これで、円で覆われている六角形の割合を計算できます（6つの円の面積を六角形の面積で割ることによって）：

$$

$$\frac{3 \pi r^2}{6 r^2 \sqrt3} = \frac{3 \pi}{6 \sqrt3} = \frac{\pi}{2 \sqrt3} \approx 0,9069$$

各六角形は約90.69％が円で覆われているため、このパッケージは正方形よりもはるかに効率的です。円の半径が予想どおりに再び消えることに注意してください。実際、これ以上効率的なパッケージはありません。



しかし、それを証明するのは簡単ではありませんでした。Joseph LouisLagrangeやKarlFriedrich Gaussなどの有名な数学者は、18世紀後半から19世紀初頭にこれに取り組み始めましたが、この問題は、周期的および非周期的なすべての可能な配置を注意深く処理することによって、1940年代にのみ完全に解決されました。すべてが非常に想像しやすい2次元で問題を解決するのに非常に時間がかかったという事実は、より高い次元で私たちを待っていることへの警告として役立つかもしれません。



球を3次元でパッキングすることは、2次元のいとこといくつかの類似点がありますが、はるかに難しい作業です。たとえば、私たちが検討した2次元パッキングは1つの層で構成されています。







正方形のパッケージの場合、各レイヤーを前のレイヤーの上に配置します。







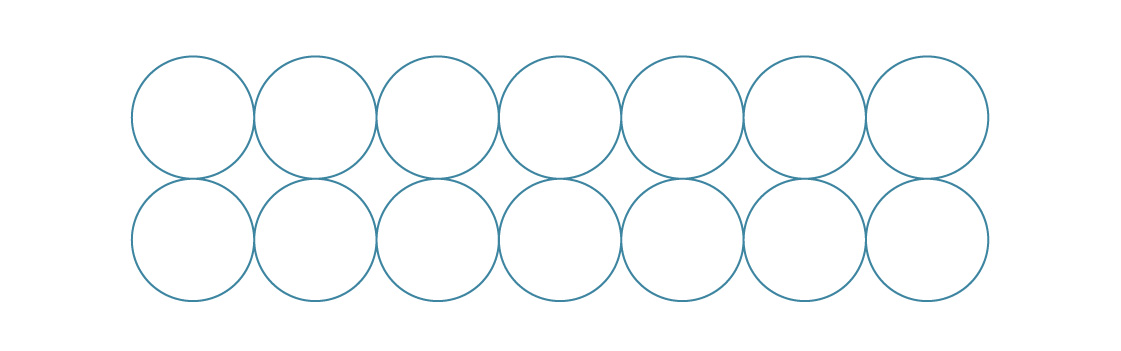
六角形のパッキングでは、前のレイヤーの間に新しいレイヤーを配置しました。







異なるレイヤーのコピーを組み合わせる方法に応じて、異なるパッケージが取得されます。



3次元では、この層の互いの配置により、根本的に異なるパッキングが作成されます。







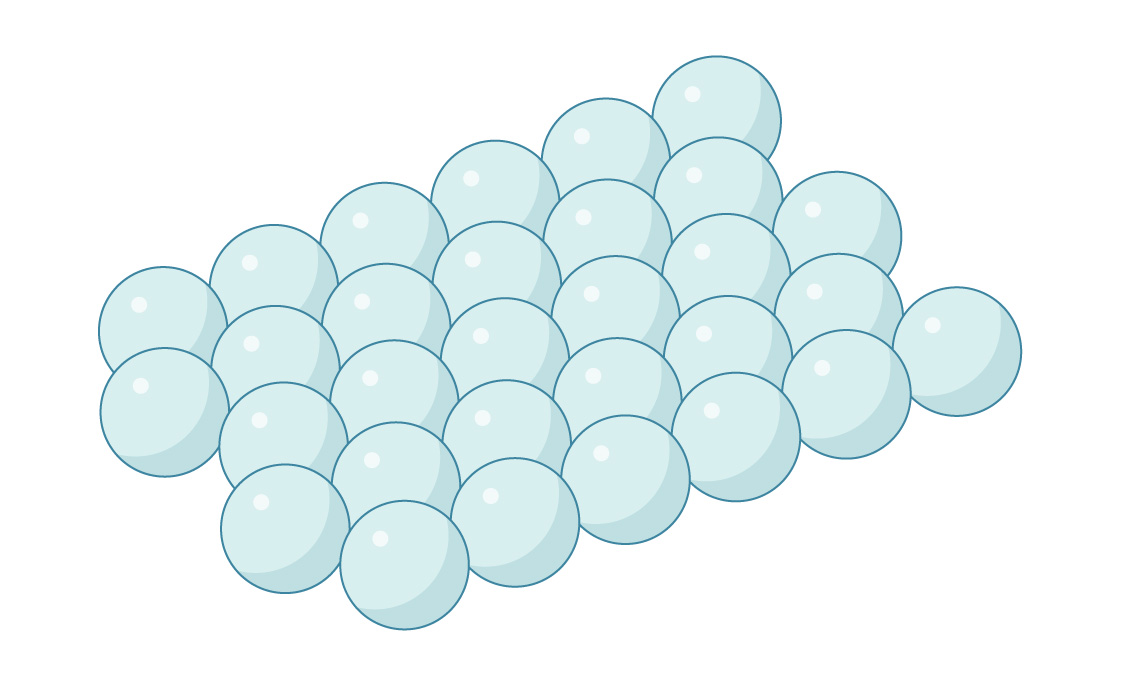
これは、平面上の円の最適なパッキングが示すように、六角形にパッキングされた球の層です。同様に、下の球の間のスペースに球を配置することにより、最初の層の上に2番目の層を配置できます。







しかし、3次元では、ジオメトリはもう少し複雑になります。球の各層では、隣接するギャップ間の距離は、球の中心間の距離よりも小さいことがわかります。したがって、各ギャップに球を貼り付けることはできません。それらは交差します。したがって、2つのレイヤーのギャップが並んで、パッケージを通過するチャネルが作成されます。







3番目のレイヤーを配置する方法は2つあります。ギャップを下のギャップに合わせて、チャネルを開いたままにすることができます。この配置の側面図を次に示し







ます。チャネルを開いたままにするには、最初のレイヤーの球のすぐ上の3番目のレイヤーに球を配置する必要があります。この球の配置は「六角形の密集」（サイロ）と呼ばれ、上から見ると隙間が開いているのがわかります。







3番目のレイヤーを配置するための別のオプションは、チャネルを閉じることです。 3番目の層の球は、最初の層のギャップの真上に配置されます。







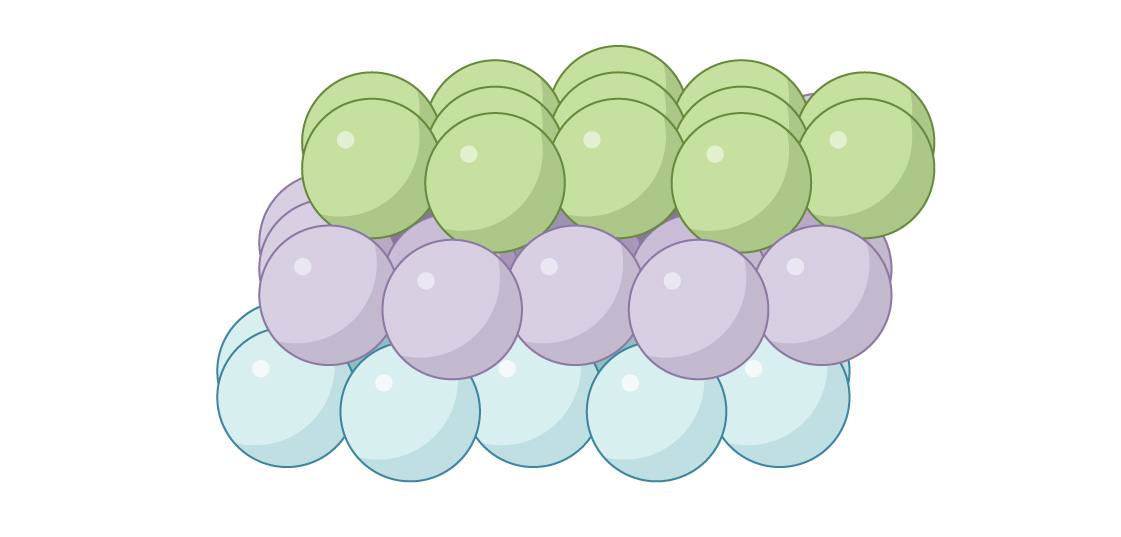
これは、「面心立方」（FCC）または「立方最密充填」と呼ばれます。上から見た場合、隙間はありません。







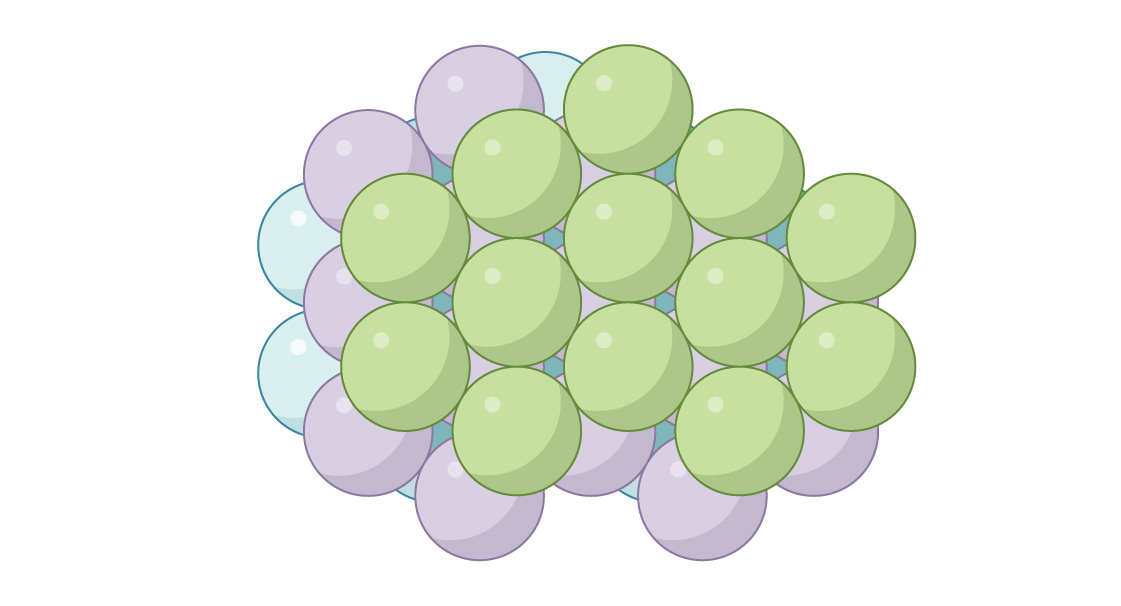
これらの2つの類似しているが根本的に異なる配置が化学で生じ、異なる材料の原子の配置を説明します。たとえば、銀や金などの金属では、構造はHAの形をしており、亜鉛やチタンなどの金属では、サイロです。 2つの方法のそれぞれで、スペースを球で埋めることができます。サイロ法では、2層ごとに球がまったく同じように配置され、GKでは3分の1ごとに配置されます。これらの両方の方法を組み合わせることで、無限の数の異なるパッケージを作成できますが、サイロとGKの両方が最適なパッケージを提供するのは興味深いことです。それらのパッキング密度は同じであるだけでなく、π3√2≈0.7405は3次元空間で可能な限り最も密度の高いパッキングです。有名な数学者で天文学者のヨハネスケプラーは1611年にこれを提案しましたが、完全な証拠です1998年に推測できたのは数学者のトーマス・ヘイルズだけでした。







3D空間にはより多くのスペースがあり、球を効果的にパックする方法が増えています。寸法を追加すると、パッケージの複雑さが増すだけです。スペースとオプションが増え、想像するのが難しくなります。また、球は高次元で小さくなります！







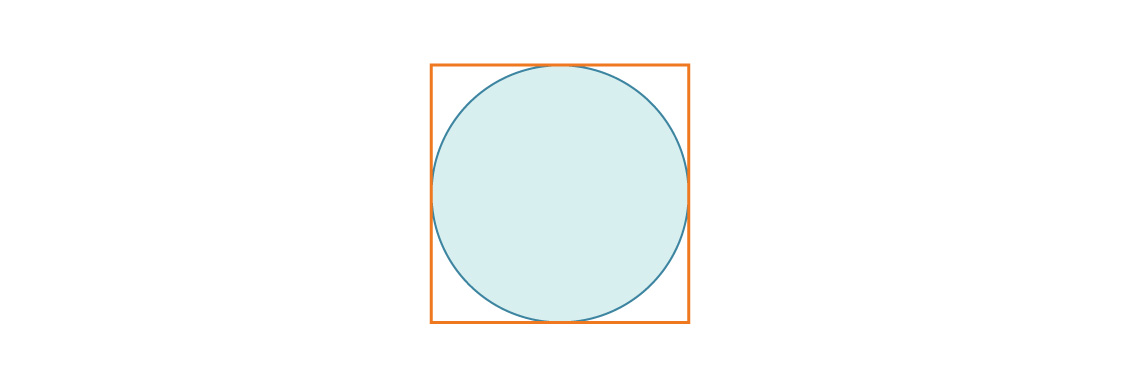
一辺の長さが1



の正方形に刻まれた円を考えてみましょう。円の半径はr = 1/2であるため、正方形の面積に対する円の面積の比率は次のようになります。

$$

$$\frac{\pi r^2}{s^2} = \frac{\pi (\frac{1}{2})^2}{1^2} = \frac{\pi }{4} \approx 0,7854$$

これは、2次元での正方形のパッキング密度にも等しくなります。



次に、ユニットキューブに刻まれた球の体積について考えてみましょう。







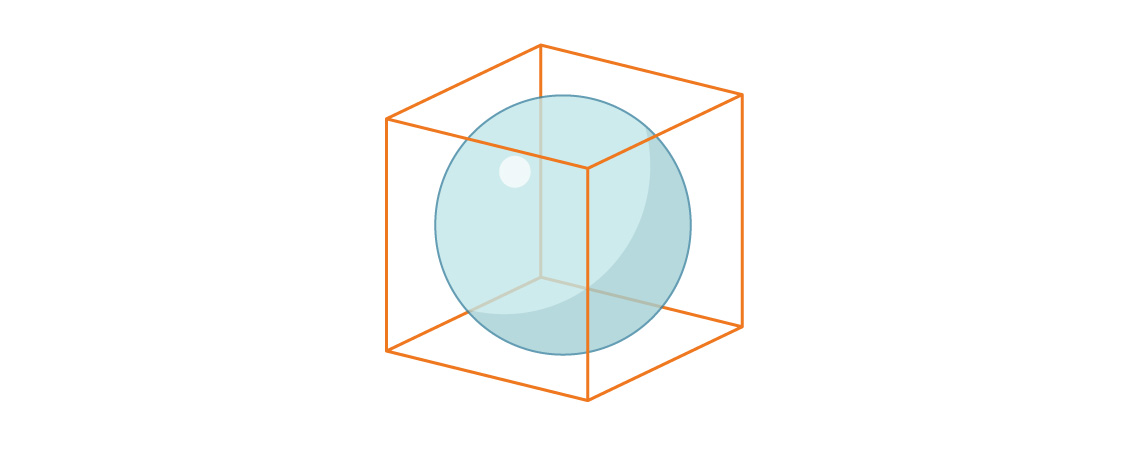
球の半径は再びr = 1/2に等しいので、球の体積と立方体の体積の比率は次のようになります。

$$

$$\frac{\frac{4}{3}\pi r^3}{s^3} = \frac{\frac{4}{3}\pi (\frac{1}{2})^3}{1^3} = \frac{4}{3}\pi (\frac{1}{8}) = \frac{\pi}{6} \approx 0,5236$$

三次元で刻まれた球が占める立方体の割合は、二次元で刻まれた円が占める正方形の割合よりも小さいことに注意してください。このパターンは続きます。寸法が大きくなると、この比率は減少します。 nが大きくなるにつれて、n次元の球が占めるn次元の空間はますます少なくなります。



これは代数を使って示すことができますが、角度を考えれば理解することもできます。どの次元でも、n次元の球をn次元の立方体に刻むことができます。球は立方体の端に接触しますが、角には到達しません。そのため、各角の周りには、立方体の内側で球の外側にある領域があります。ただし、n次元のボックスには^{2nがあります}角度、つまりnが大きくなると、球で覆われていない領域の数が指数関数的に増加します。さらに、コーナーと球の間の距離も増加します。これは、長期的には、n次元の立方体の内側であるが、n次元の球の外側の空間は、球が占める空間を単純に押しつぶすことを意味します。



球の収縮があなたにとって十分に奇妙に思える場合、球のパッキングに関与する数学者は、次元8と24でさらに予期しない何かに気づきました。これらの次元では、球は新しい球の間のギャップを埋めることができるのに十分に収縮し、これらの次元で超高密度のパッキングを提供します。 ..。これらの特別な方法の最適性について仮説が提唱されましたが、MarinaVyazovskaya がこの定理を証明した2016年まで確実に知られていませんでした。8次元空間用。1週間後、Vyazovskayaと彼女のアシスタントは、24次元空間のケースも証明するための彼女の方法を拡張しました。



Vyazovskayaの研究から、次元1、2、3、8、および24で球をパッキングする最も効率的な方法がわかったことがわかります。しかし、他の次元では、まだやるべきことがたくさんあります。だから、オレンジとソーダ缶を取り出して、実験を始めてください。あなたは重要なギャップを埋めることができる人かもしれません。

演習

1.下の写真に示すように、座標平面のパッキングを開始したとしましょう。左下の円の中心は点（0、0）にあり、右下の円の中心は点（2、0）にあります。







3番目の円の中心はどこですか？



2.以下は、球の「単純な立方体」パッキングの始まりです。そのようなスキームのパッキング密度はどれくらいですか？







3.これが平面を通常の八角形に詰め込むことの始まりです。







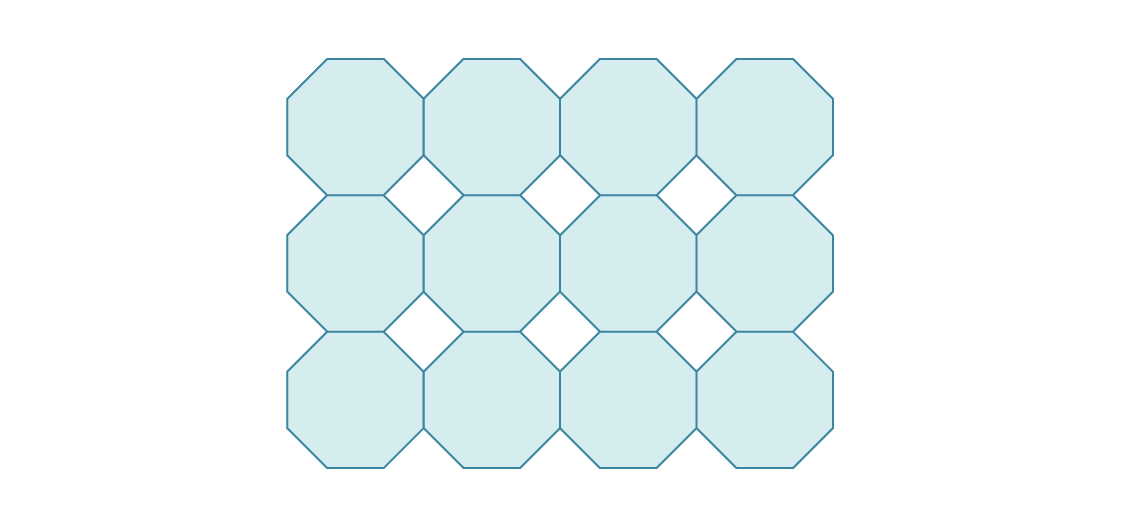
そのようなパッケージの密度はどれくらいですか？

回答

参照：

• 「Googleがソーシャルディスタンスを表示するためのARツールであるSodarをリリース」
• 「メタスタディは、SARS-CoV-2（COVID-19）に対するマスクと距離の有効性を明らかにします。」
• 「COVID-19：流行パラメトリック予測モデル」